N皇后问题——回溯求解一般方法（C语言）

一、问题描述

        八皇后问题十分经典，也就是每两个棋子之间不能处于同一行、同一列、同一对角线。

        此类问题，可以视作在约束条件下进行先序（根）遍历，并在遍历过程中剪去那些不满足条件的分支。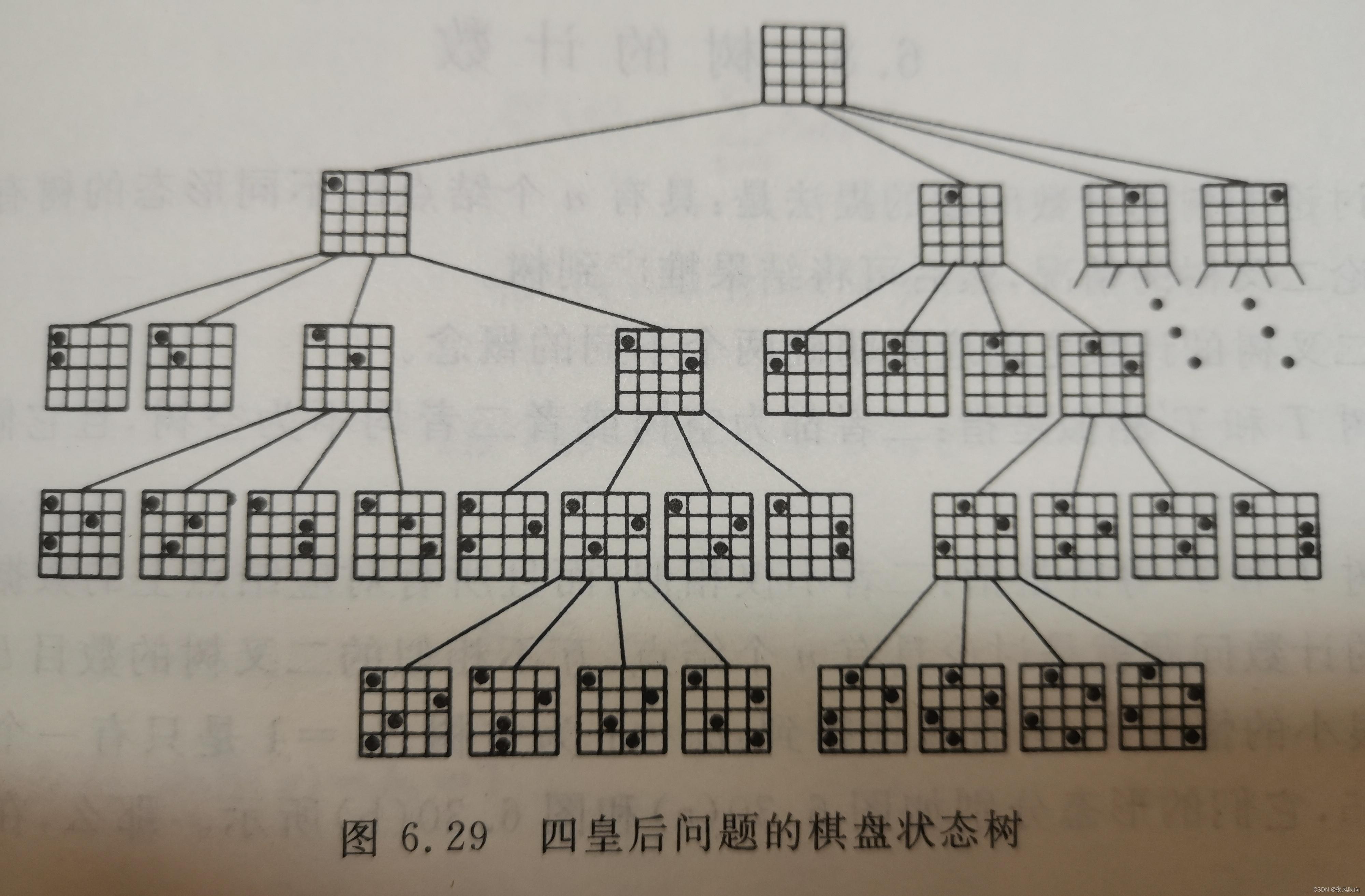

        如图，就是一个四皇后问题的棋盘状态树，可以看到，在递归过程中不仅有落子行为，还有剪枝行为。

二、问题思路

        可以采用回溯求解的一般思路，以下是书本上的伪代码思路。

void Trial(int i, int n) {
    // 当进入本函数时，在nxn的棋盘的前i-1行已有满足条件的i-1个棋子
    // 现从第i行开始为后续棋子选择位置
    // 当i>n时，即为合法布局，输出之

	if(i>=n)  出现符合的棋局，输出结果 
	else {
        for(j = 1; j<=n; j++) {
			在第i行j列放棋子
			if(当前布局合规) Trial(i+1, n);
			移除第i行j列的棋子
		}
	}
}

三、具体实现

        其中 i 是行，从 0 开始计数；n 代表每行最大元素数目；board是棋盘数组，由于二维数组的存储可以视为一维数组，因此可以用 board[n*i +j] 表示第 (i, j) 号元素。

//到第 i 行都放了合规的棋子
void Queen(int i, int n, int* board) {
	if(i>=n) {     //出现符合的棋局，输出结果 
		sum += 1;  //统计有多少解法
		printf("result:%d\n", sum);
		for(int x = 0; x<n*n; x++) {
			printf("%d ", board[x]);
			if((x + 1) % n == 0) puts("");
		}
	} else {
		for(int j = 0; j<n; j++) {
			board[i*n + j] = 1;  //放皇后 
			if(NoUp(i, j, n, board) && NoDia(i, j, n, board))  //当符合规范，递归放皇后 
				Queen(i+1, n, board);
			board[i*n + j] = 0;  //移除皇后 
		}
	}
}

在检测当前棋局是否合规时，由于是从上往下放棋子，因此只需要判断 (i, j) 上方是否有棋子即可。

完整代码如下

#include<stdio.h>

#define MaxSize 12

//计数
int sum = 0;

//检测(i, j)上方元素是否有冲突
bool NoUp(int i, int j, int n, int* board) {
	for(int x = 0; x<i; x++) {
		if(board[x*n + j] == 1) return false;
	}
	return true;
}

//检测(i, j)对角线上元素是否有冲突
bool NoDia(int i, int j, int n, int* board) {
	int flag = 0;
	while(i-flag > 0) {   //当(i, j)不在第一行时
		flag += 1;
		if(j-flag >= 0) { //检测位置是否超边界，处于左上方对角线的元素是否冲突
			if(board[i*n + j - (n+1) * flag] == 1) return false;
		}
		if(j+flag < n) {  //检测位置是否超边界，处于右上方对角线的元素是否冲突
			if(board[i*n + j - (n-1) * flag] == 1) return false;
		}
	}
	return true;
}

//到第 i 行都放了合规的棋子
void Queen(int i, int n, int* board) {
	if(i>=n) {     //出现符合的棋局，输出结果 
		sum += 1;  //统计有多少解法
		printf("result:%d\n", sum);
		for(int x = 0; x<n*n; x++) {
			printf("%d ", board[x]);
			if((x + 1) % n == 0) puts("");
		}
	} else {
		for(int j = 0; j<n; j++) {
			board[i*n + j] = 1;  //放皇后 
			if(NoUp(i, j, n, board) && NoDia(i, j, n, board))  //当符合规范，递归放皇后 
				Queen(i+1, n, board);
			board[i*n + j] = 0;  //移除皇后 
		}
	}
}

int main() {
	int board[MaxSize*MaxSize] = {0};  //棋盘初始化 

	Queen(0, MaxSize, board);

	return 0;
}

四、后记

        通过修改MaxSize的大小，可以拓展到N皇后问题。

        在测试过程中，12皇后解的数目达到了5位数，而10皇后的解的数目只有3位数。