机器学习4-多元线性回归

多元线性回归(Multiple Linear Regression)是线性回归的一种扩展形式，用于建立因变量与多个自变量之间的关系。在简单线性回归中，我们考虑一个因变量和一个自变量之间的线性关系，而多元线性回归允许我们考虑多个自变量对因变量的影响。

一般的多元线性回归模型的数学表达式如下：

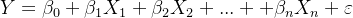
$Y=\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+...++\beta_{n}X_{n}+\varepsilon$

其中：

Y 是因变量（要预测的目标）。
X1,X2,…,Xn 是自变量（特征）。
β0 是截距（模型在X1,X2,…,Xn 都为0时的预测值）。
β1,β2,…,βn 是各自变量的回归系数，表示自变量对因变量的影响。
ε 是误差项，表示模型无法捕捉到的影响因素和随机误差。

多元线性回归的目标是找到合适的回归系数 β0,β1,…,βn 来最小化实际观测值 Y 与模型预测值之间的误差，通常使用最小二乘法进行优化。

模型训练后，可以使用这个模型进行预测。当有新的自变量值 X1,X2,…,Xn 时，通过带入这些值，就可以预测相应的因变量值 Y。

多元线性回归在实际应用中非常常见，例如在经济学中预测商品销售额，医学中预测疾病发生率，工程学中预测产品性能等。

需求：

根据现有数据预测公司的利润

数据示例：

R&D Spend	Administration	Marketing Spend	State	Profit
165349.2	136897.8	471784.1	New York	192261.83
162597.7	151377.59	443898.53	California	191792.06

程序：

## Step 1: Data Preprocessing

### Importing the libraries
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

### Importing the dataset
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :-1].values
Y = dataset.iloc[:, 4].values

### Encoding Categorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.compose import ColumnTransformer

labelencoder = LabelEncoder()
X[:, 3] = labelencoder.fit_transform(X[:, 3])

# Use ColumnTransformer for one-hot encoding
ct = ColumnTransformer(
    transformers=[
        ('onehot', OneHotEncoder(), [3])  # Apply one-hot encoding to column 3
    ],
    remainder='passthrough'  # Keep the rest of the columns unchanged
)

X = np.array(ct.fit_transform(X), dtype=np.float64)

### Avoiding Dummy Variable Trap
X = X[:, 1:]

### Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

## Step 2: Fitting Multiple Linear Regression to the Training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)


## Step 3: Predicting the Test set results
Y_pred = regressor.predict(X_test)

print(Y_pred)

# Step 4: Visualizing the results
plt.scatter(Y_test, Y_pred, color='blue')
plt.plot([min(Y_test), max(Y_test)], [min(Y_test), max(Y_test)], linestyle='--', color='red', linewidth=2, label='Regression Line')

plt.title('Actual vs Predicted Profit')
plt.xlabel('Actual Profit')
plt.ylabel('Predicted Profit')
plt.show()

结果：

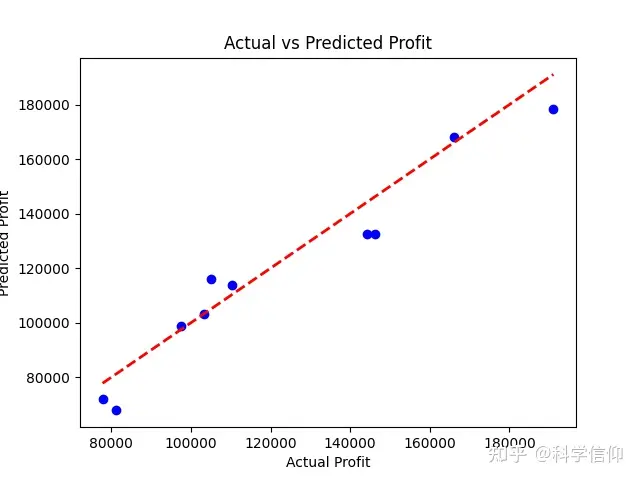
结论：

10个结果数据的预测值与真实值相差不多，大体落在线性回归模型的范围内。