前言
- hello,大家好,我是 Lorin,这将是数据结构系列文章的开始,大家可以根据自己的实际情况选择合适章节食用。
二叉树
- 二叉树是计算机科学中最基本且重要的数据结构之一。它在许多算法和数据处理中都有广泛的应用,包括操作系统、编译器、数据库系统、图形学,甚至是人工智能。在本文中,我们将深入探讨二叉树的基本概念、特性以及在编程和算法中的应用。
定义
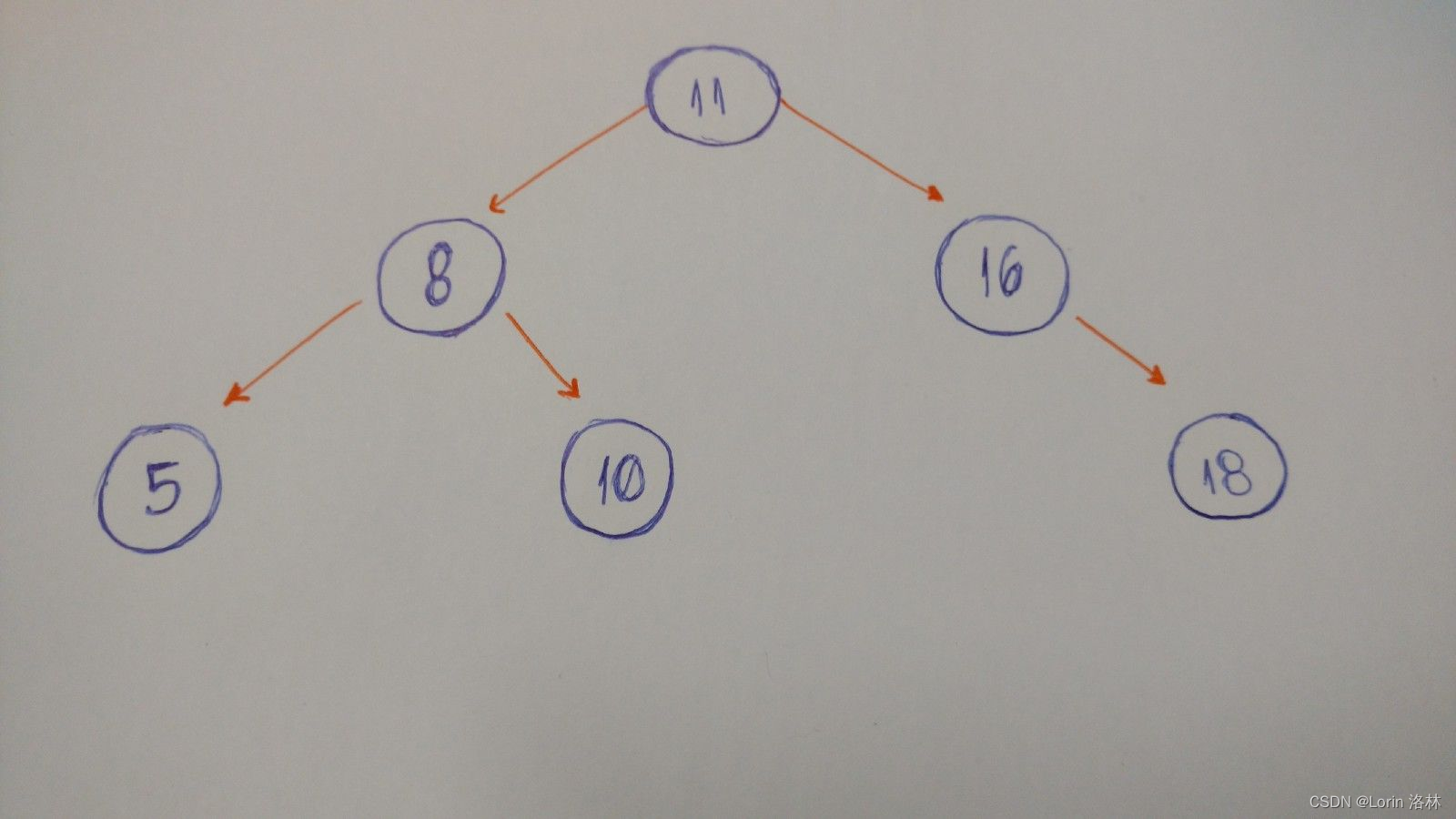
- 二叉树是由节点组成的树状数据结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树具有以下特点:
每个节点最多有两个子节点,分别为左子节点和右子节点。
每个节点都有一个父节点,除了根节点。
二叉树的每个节点可以包含一些数据或值。
类型
- 二叉树有多种不同的类型,其中一些常见的类型包括(后面的文章我们会具体介绍):
二叉查找树(Binary Search Tree,BST)
- 在BST中,左子树的所有节点的值都小于根节点的值,右子树的所有节点的值都大于根节点的值。这个性质使得BST非常适合进行快速的搜索和排序操作。
平衡二叉树
- 平衡二叉树是一种特殊的BST,它的左右子树高度差不超过1。这保证了树的高度相对较低,从而提高了搜索和插入操作的性能。
红黑树(Red-Black Tree)
- 红黑树是一种自平衡的BST,它通过一系列规则来保持树的平衡。它是一种高效的数据结构,用于实现诸如集合、映射等数据结构。
二叉树的遍历
深度优先遍历(DFS)
前序遍历(Preorder Traversal)
中序遍历(Inorder Traversal)
- 从根节点开始,按照左、根、右的顺序遍历树的节点。在BST中,中序遍历会按升序访问所有节点。
后序遍历(Postorder Traversal)
广度优先遍历(BFS,层次遍历)
- 从根节点开始,逐层遍历树的节点,先左后右。通常使用队列来实现。
二叉树遍历实现 Java 版
import java.util.Queue;
import java.util.concurrent.ArrayBlockingQueue;
class TreeNode {
Integer val;
TreeNode left, right;
public TreeNode(Integer val) {
this.val = val;
}
}
public class Test2 {
public static void main(String[] args) {
TreeNode root = new TreeNode(11);
root.left = new TreeNode(8);
root.right = new TreeNode(16);
root.left.left = new TreeNode(5);
root.left.right = new TreeNode(10);
root.right.right = new TreeNode(18);
dlr(root);
System.out.println();
ldr(root);
System.out.println();
lrd(root);
System.out.println();
bfs(root);
}
private static void dlr(TreeNode root) {
if (root != null) {
System.out.print(root.val + " ");
dlr(root.left);
dlr(root.right);
}
}
private static void ldr(TreeNode root) {
if (root != null) {
ldr(root.left);
System.out.print(root.val + " ");
ldr(root.right);
}
}
private static void lrd(TreeNode root) {
if (root != null) {
lrd(root.left);
lrd(root.right);
System.out.print(root.val + " ");
}
}
private static void bfs(TreeNode root) {
Queue<TreeNode> queue = new ArrayBlockingQueue<>(10);
if (root == null) {
return;
}
queue.add(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
System.out.print(node.val + " ");
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
}
二叉树的应用场景
- 在实际场景使用中,并不会用最基本的二叉树,而是基于二叉树的变体,比如平衡树、红黑树、B树或B+树等等来满足我们不同的需求场景。
- 二叉树在计算机科学中有广泛的应用,其中一些包括:
数据搜索和排序
- 二叉查找树用于快速搜索和排序数据。它们在数据库索引、电话簿等应用中非常有用。
文件系统
- 操作系统中的文件系统通常使用树的结构来组织和管理文件。
编译器
- 编译器和解释器使用抽象语法树(Abstract Syntax Tree,AST)来表示程序的结构,以便进行分析和优化。
其它
- 接下来将分享一系列数据结构相关文章,希望感兴趣的朋友可以多多点赞关注支持。
