【论文简述】GeoMVSNet: Learning Multi-View Stereo with Geometry Perception(CVPR 2023)
一、论文简述
1. 第一作者:Zhe Zhang
2. 发表年份:2023
3. 发表期刊:CVPR
4. 关键词:MVS、级联结构、几何感知、频域增强、高斯混合模型
5. 探索动机:基于级联的结构以从粗到细的方式计算不同分辨率的深度图,并逐步缩小假设平面指导,以降低计算复杂度。然而,这些方法并不考虑早期阶段所包含的有价值的洞察,只考虑像素级深度属性。 一些方法,例如基于可变形核和基于transformer,引入了更精细的设计过的外部结构来进行特征提取,但没有充分利用嵌入MVS场景中的几何线索。
6. 工作目标:虽然最近的一些工作试图通过变形卷积或多尺度信息聚合来获得大上下文,但对于MVS,还没有探索在每个视图中挖掘全局上下文的解决方案。此外,探索一种获取三维一致性特征的方法对于MVS中鲁棒可靠的匹配至关重要。
7. 核心思想:
- We propose the geometric prior guided feature fusion and the probability volume geometry embedding approaches for robust cost matching.
- We enhance geometry awareness via the frequency domain filtering strategy and adopt the idea of curriculum learning for progressively introducing geometric clues
from easy to difficult.- We model the depth distribution of MVS scenarios using the Gaussian-Mixture Model assumption and build the full-scene geometry perception loss function.
8. 实验结果:
The proposed method is extensively evaluated on the DTU dataset and both intermediate and advanced sets of Tanks and Temples benchmark, all achieving brandnew state-of-the-art performance.
9.论文下载:
二、实现过程
1. GeoMVS-Net概述
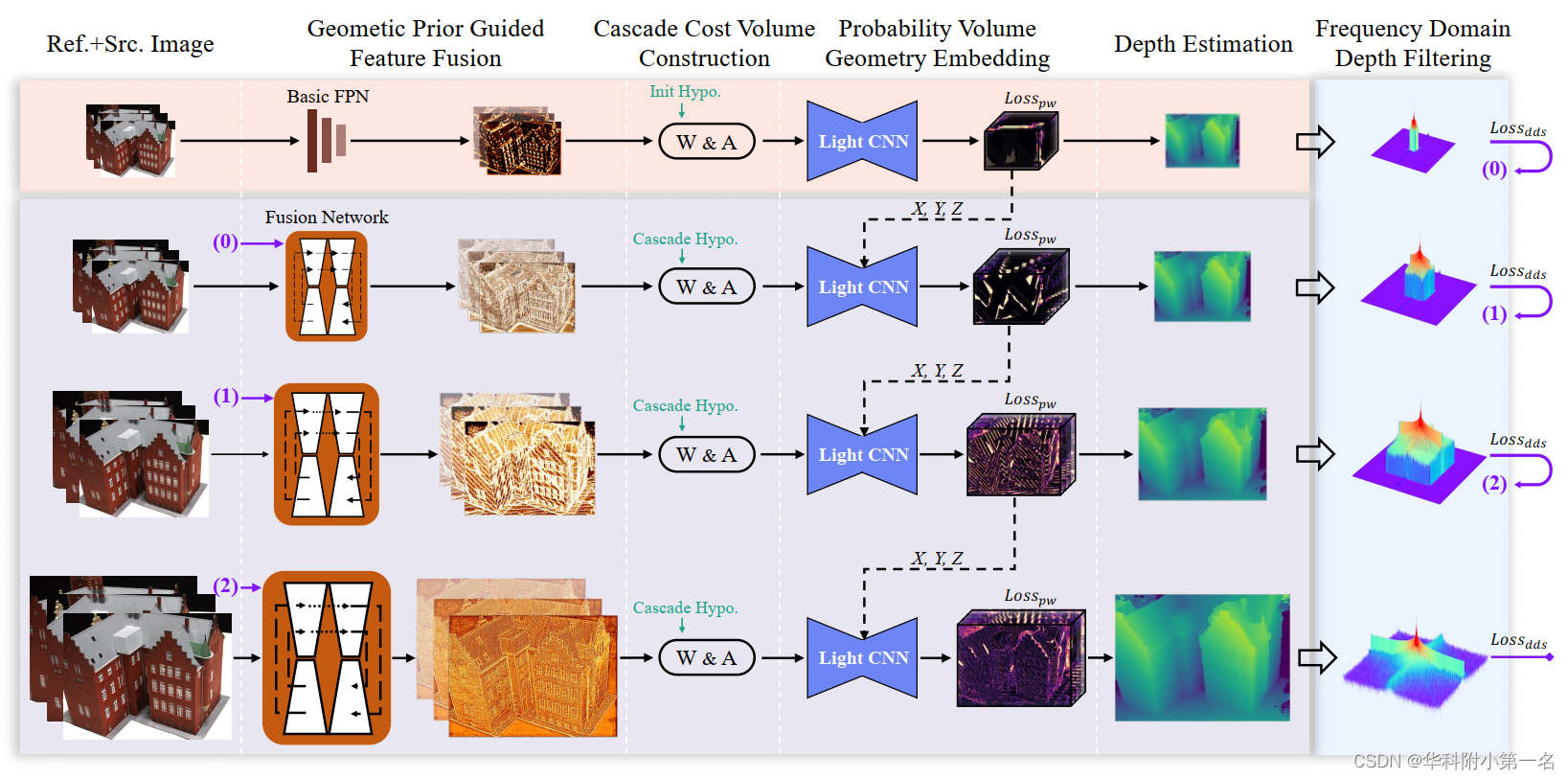
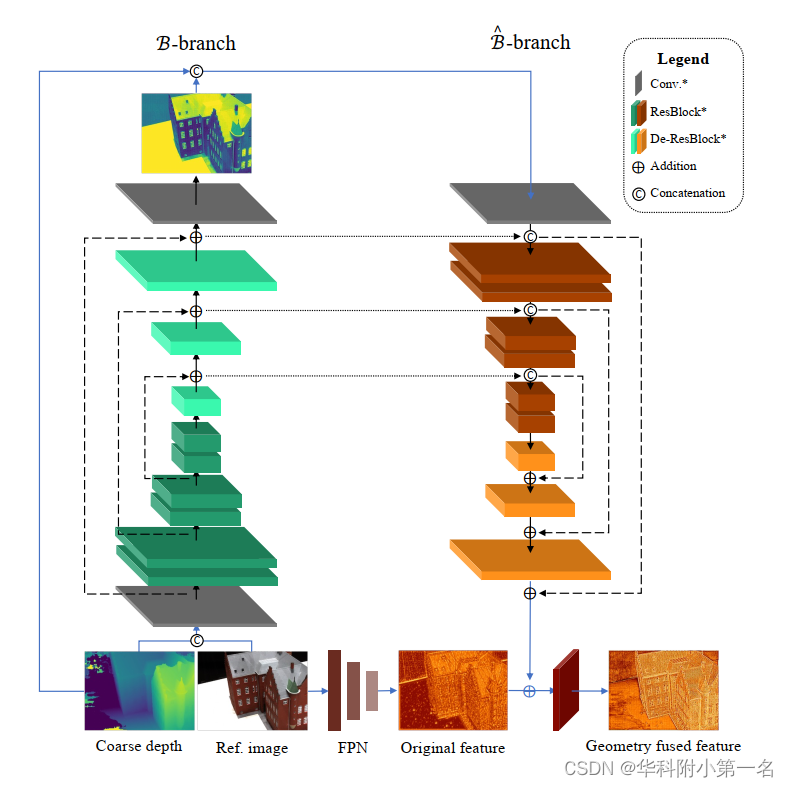
总体架构见图。在水平数据流中,首先通过几何融合网络从输入图像中提取的深度图像特征Fi,单应性变化得到特征体Vi。然后将多个特征体聚合为单个代价体C∈G×M×H×W,其中G为组相关通道。然后对C进行轻量级代价正则化,得到概率体P∈M×H×W,表示像素的可能性“粘”在深度平面上,用于几何感知。基于高斯混合模型的深度分布相似度损失和具有课程学习策略的频域滤波用于全场景几何增强。前一阶段的几何先验输出用于指导更精细阶段的几何感知,如数字标签(0)~(2)所示。
2. 鲁棒代价匹配的几何感知
MVSNet及相关工作中代价匹配的聚合和正则化过程比传统的利用归一化互相关(NCC)来测量图像块相似度MVS方法更具鲁棒性。然而,在最流行的级联MVS方案中,不同阶段的图像特征和代价体通常具有相同的成分,这不能充分挖掘早期阶段提供的广泛几何信息。与现有的依赖于费力的外部依赖的工作不同,本文建议明确地融合粗深度估计的几何先验,并将粗阶段的粗概率体嵌入到细阶段的代价匹配中。
几何先验引导特征融合。以l和l+1层为例,在更精细阶段的参考图像的几何先验引导的特征表示为:
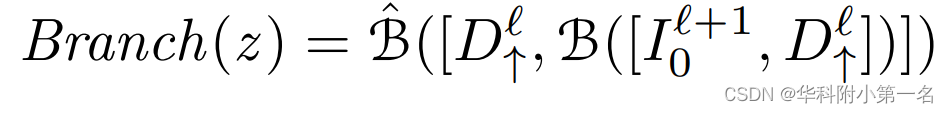
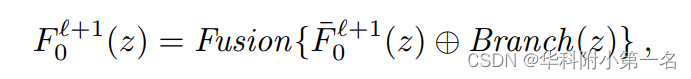
其中z表示图像像素,[:,:]和⊕分别表示连接和逐元素相加操作。双分支网络结构在深度补全任务中得到了很好的研究。在这里,通过两个神经子模块B和B~融合参考图像的纹理和之前粗深度的上采样几何先验,并将该组合称为Branch。然后,通过经典FPN得到的特征F0r+1通过Fusion网络合融合。下图给出了用于结构特征提取的几何融合网络的结构。可以清楚地看到,与参考图像对齐的几何先验被显式地编码到基本的FPN特征,几何融合的参考特征可以与各向异性源特征进行鲁棒匹配。
概率体几何嵌入。如前所述,概率体P表示某个像素的深度假设的可能性。现有的基于金字塔的方法没有充分利用Pi包含的大量洞察力,而只是使用它派生的粗深度图来减少更密集的空间划分的计算消耗。由于概率体在不同阶段的尺度和空间范围不同,可以使用Pi作为嵌入到代价正则化网络中的三维“位置图”,而不像特征融合那样将它们分解成代价体的构建。特别是,在三维代价正则化网络中,将卷积核大小从k × k × k减小到1 × k × k,其中第一维表示深度方向。同时,在深度方向上由于缺乏庞大但功能强大的三维卷积而造成的缺陷被明确的粗概率体嵌入所弥补。
首先将粗阶段的Pl经过多个3D Maxpooling层,构建不同稀疏率的几何感知金字塔。然后将它们显式编码到不同较大的感受野寻找,U-Net的跳跃连接层形成轻量级正则化网络,以构建融合的空间相关性。3D几何位置嵌入的数学表达式为:
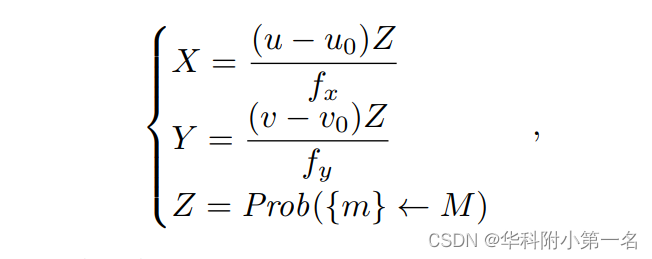
其中(u, v)为M个预定义总深度平面中第M个候选假设中的体素的像素坐标,u0, v0, fx, fy为相机内参的一部分。从粗糙到精细的阶段的概率体的几何嵌入如图所示,其中沿深度方向的几何嵌入切片编码了关于场景整体结构的空间感知,而不仅仅是提供像素级的“置信度”。在网络中连续传递细粒度几何感知,实现鲁棒的代价匹配。(a)从粗到细的嵌入过程概述:(b)由不同阶段的概率体得出的几何感知的基础。

几何先验引导的特征融合在不引入外部复杂依赖的情况下,在更精细的阶段加强了深层特征的区别性和结构,为鲁棒聚合奠定了坚实的基础。嵌入概率体不仅提供体素坐标和深度感知位置编码,实现鲁棒的代价体正则化,而且还将全场景深度分布特征引入到更精细层的深度感知中。
3. 频域几何增强
粗深度图融合和概率体嵌入可以有效地将逐步增强的几何感知融入到代价匹配中。尽管如此,对粗糙深度图中固有的杂乱纹理的严重错误估计,例如帧中的无限天空和图像边缘附近的区域,重投影极容易出界,不可避免地增加了融合网络和代价正则化网络的学习负担。
为了修复严重错误的深度值,尝试使用预训练的RGB引导的深度改进模块。插件深度优化模块确实在视觉上润色深度图,特别是在物体轮廓处。然而,对深度图进行光谱分析如图4 (a),发现润色后的深度具有明显更高的频率信息,这给网络学习带来了负担。更重要的是,看似准确
“改进”操作降低了几何一致性约束的满意度,导致点云的整体质量显著恶化(0.200 vs . 0.704)。主要原因是RGB引导的深度优化倾向于拟合数据集中的深度分布,而MVS通过匹配来估计几何上一致的深度。
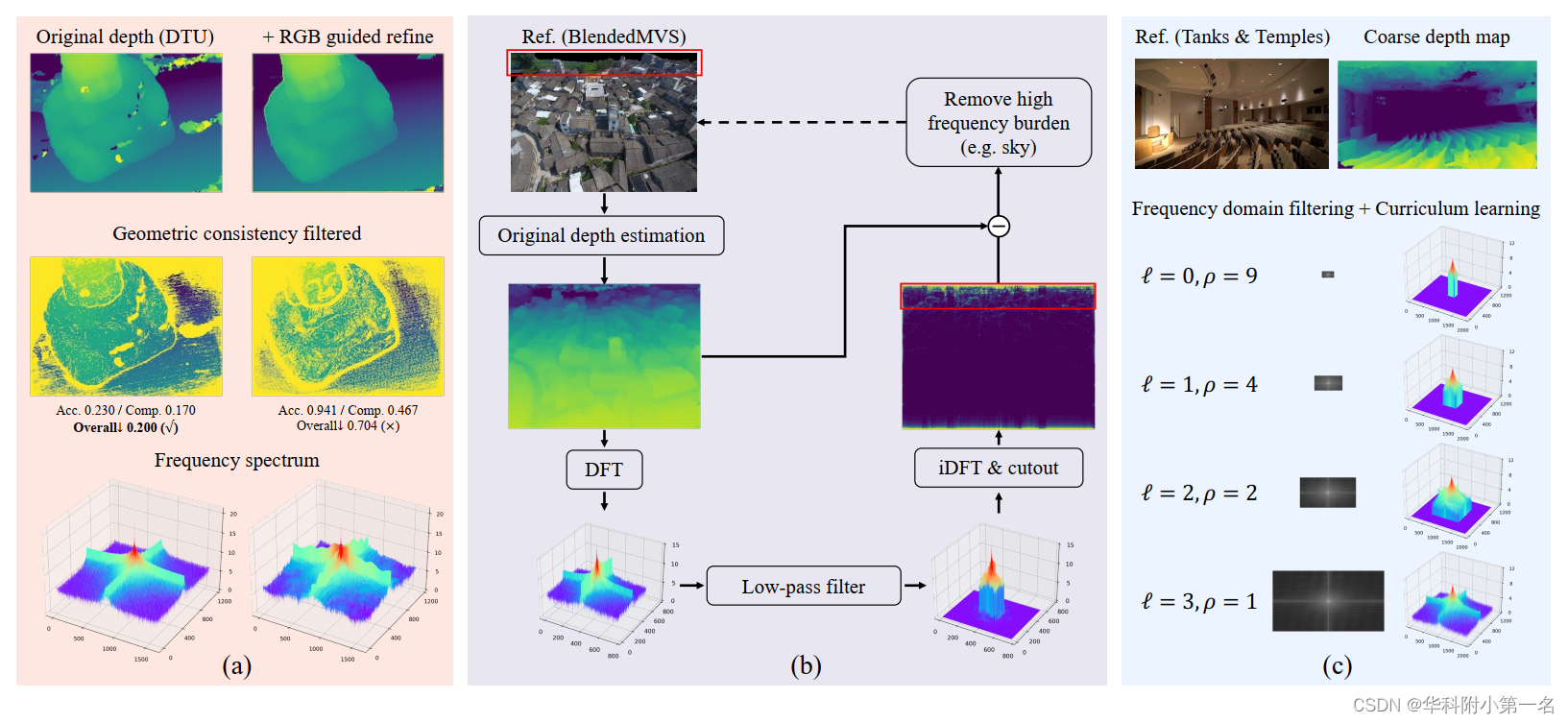
相反,通过离散傅里叶变换使用频域滤波来解决问题(DFT)。将粗深度图视为二维离散信号,并通过方程将其变换到频域,其中j是虚单位。
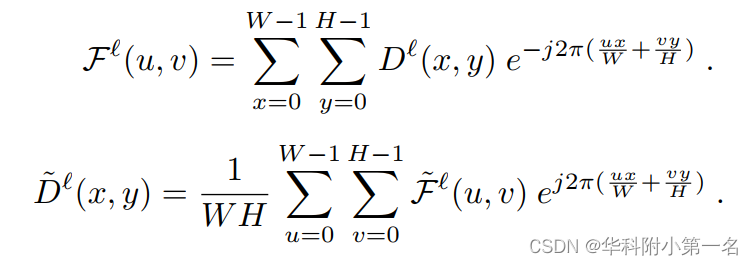
在FFT-shift之后,如图(b)用一个基础理想的矩形低通滤波器从粗深度图中消除高频信息,式用于逆域转换。简单而有效的频率滤波巧妙地从显式建模的粗几何嵌入中去除复杂和不可理解的知识,同时避免产生更多的学习参数。 同时,在不使用手工标记的视觉掩码的情况下,严重的错误估计和高频负荷信号得到了缓解,使网络能够更专注于全场景几何感知。
此外还参考了课程学习的思想,在教学困难的深度嵌入样本融合网络和代价正则化网络。设Dℓ定义为第l阶段估计深度图Dℓ的随机变量,并且场景的目标分布为N。设0≤Wl(dl)≤1是应用于课程序列中示例 dl 的权重。训练分布为:
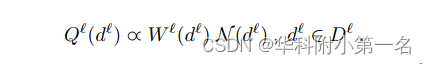
通过调制频域滤波器的截断核比(ρ)来调节单调的递增权值Wℓ,并保留从粗到细方案的最后阶段的未装饰的几何线索(ρ=1)。课程学习策略如图所示(c)为代价正则化网络引入了更好的几何线索消费模式,有效增强了MVS网络的全场景几何感知能力。
4. 混合高斯深度分布模型
基于sfm算法的稀疏重建给定预估深度范围[dmin, dmax],现有的基于学习的MVS方法始终遵循均匀深度分布假设,将参考相机截锥体划分为M个深度假设平面。CIDER提出在逆深度空间中划分假设平面,Yang引入了多模态深度分布。然而,这些方法只考虑像素深度特性,而没有模拟全场景深度分布,这是几何感知的关键。
目前研究中需要重建的场景可分为三类:a)中心物体和绕转相机;B)周围物体和自旋转相机;C)航拍照片。下图显示了BlendedMVS数据集上每个类别的图像和全场景深度分布。自然场景的深度范围往往集中在几个特定的区域,太近和太远的位置隐藏在深度分布曲线的长尾中。

根据观察,假设随机变量深度值d符合高斯混合模型(GMM)分布。样本分布可以建模为N (d;µi,σi2),其中θi={µi,σi}分别为第i个高斯分量的均值和标准差。概率密度函数由:
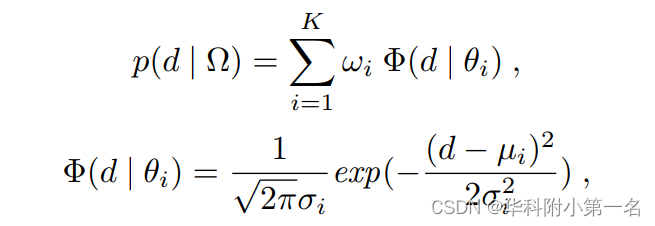
式中Ω={wi},i=(1,2,…,K)是模拟了变量d落在近似估计区间内满足约束的概率的先验分布集,满足约束条件:
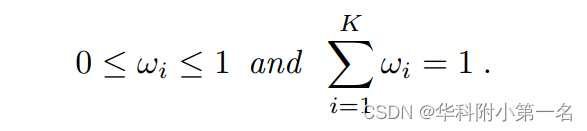
在K=1或2时,大多数场景都可以很好地描述,只有少数场景可以用K≥3时的分布来建模。而PauTa准则允许在几个(µi−3σi,µi+3σi)区间的组合内很好地描述整个场景的深度分布。无穷点的长期负担(例如:天空)不会给学习带来负面影响当采用PauTa准则的GMM,可以更好地利用全场景深度分布增强空间感知。
5. 损失函数
基于像素的分类建模更适合本文表示,因为回归模型和最近发表的联合模型在早期阶段往往会陷入局部最优解。逐像素监督的交叉熵损失为:
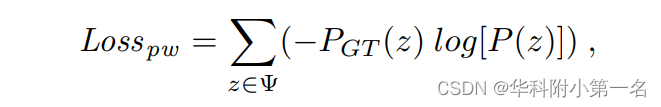
其中Ψ为具有真实精度的有效像素集,PGT为真实概率体。
此外,全场景深度分布的感知是本文研究的重点。使用Kullback-Leibler散度度量来计算滤波深度估计和真实深度之间样本分布的相似度。深度分布相似度损失为:
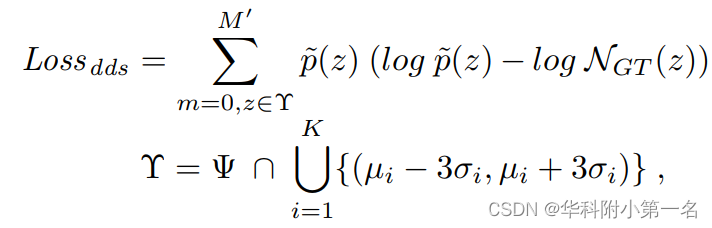
其中p ~(:)表示过滤后的深度分布,将每个场景的深度空间分割为M′= 48个离散区间,计算深度分布的相似度。
总损失是Losspw和Lossdds的权重加权和,λ∗1=0.8,λ∗2=0.2。
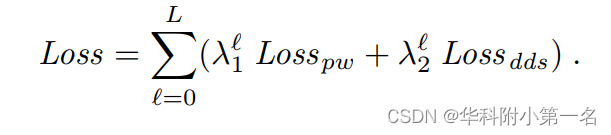
6. 实验
6.1. 实现细节
Our model consumes 0.26s and 5.98G memory for the full-resolution DTU depth estimation and 0.47s and8.85G memory for the T&T. As for depth fusion, we use the open-source 3D data processing library Open3D for dense point cloud fusion for the DTU, and adopt the commonly used dynamic fusion strategy for the T&T.
6.2. 与先进技术的比较
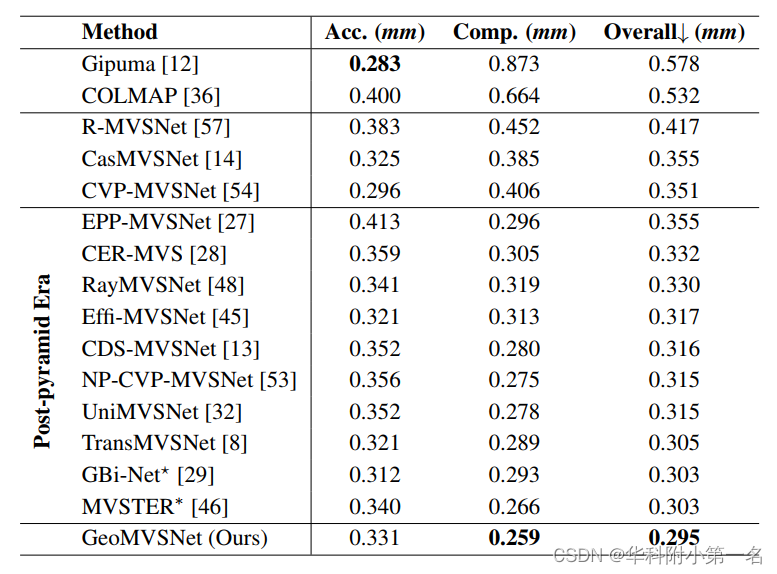
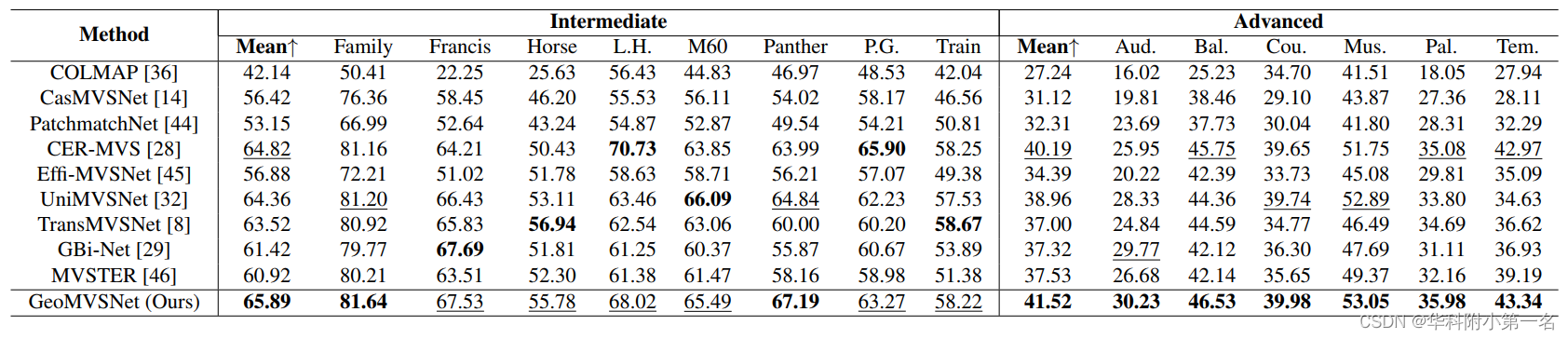
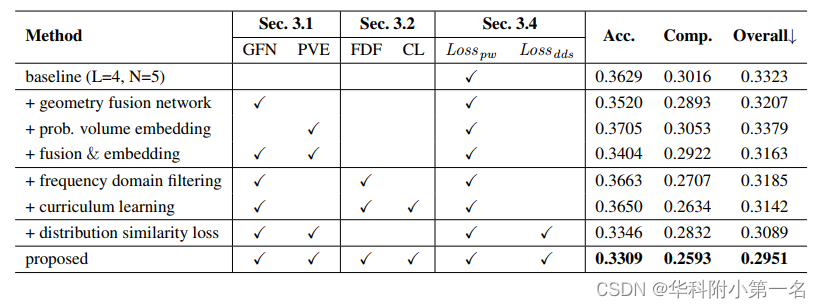
6.3. 消融实验