【数据分析】numpy基础第三天

前言

本文只会讲解最常用的加、减、乘、除，点乘（或叫矩阵乘法）、还有广播机制。

本文代码

• 链接
• 提取码：1024

第1部分：基础数学计算

使用NumPy进行基本的数学运算是十分直观和简单的。下面我们将展示一些基本的加、减、乘、除运算。

和一个数字加减乘除

让我们首先创建一个简单的数组：

import numpy as np

arr = np.array([[1, 2],
                [-1, 4]])

现在，我们将展示如何把一个整数与数组中的每个元素进行加减乘除。

和整数3的乘法

arr * 3

该操作将会输出：

array([[ 3,  6],
       [-3, 12]])

和整数3的加法

arr + 3

该操作将会输出：

array([[4, 5],
       [2, 7]])

和整数3的减法

arr - 3

该操作将会输出：

array([[-2, -1],
       [-4,  1]])

和整数3的除法

arr / 3

该操作将会输出：

array([[ 0.33333333,  0.66666667],
       [-0.33333333,  1.33333333]])

相同形状矩阵之间的加减乘除

当两个矩阵形状相同，NumPy允许进行元素级的运算。

相同形状矩阵之间的乘法

A = np.array([[1, 2], [-1, 4]])
B = np.array([[2, 0], [3, 4]])

A * B

输出结果是：

array([[ 2,  0],
       [-3, 16]])

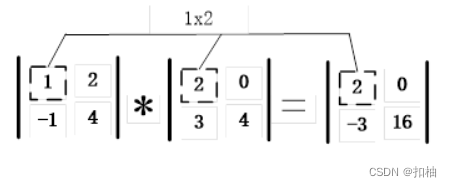
以上代码执行的逻辑相当于对矩阵的对应位置的元素进行相乘，如下图所示，其余的加法、减法、除法的也是同理。

图1

相同形状矩阵之间的加法

A + B

输出结果是：

array([[3, 2],
       [2, 8]])

相同形状矩阵之间的减法

A - B

输出结果是：

array([[-1,  2],
       [-4,  0]])

相同形状矩阵之间的除法

A / B  # 不必担心这里的红色警告，请看下文，这并不是你的问题。

在Numpy的除法运算中，如果除数中包含0，则会收到警告，但程序不会停止，该位置的结果会是无穷（inf）。

输出结果是：

array([[ 0.5       ,         inf],
       [-0.33333333,  1.        ]])

点乘

点乘（dot product）或矩阵乘法在NumPy中非常重要，但是在数据分析上应用较少，了解即可。

X1 = np.array([[1, 2], [3, 4]])
X2 = np.array([[5, 6, 7], [8, 9, 10]])

X3 = np.dot(X1, X2)

输出结果是：

array([[21, 24, 27],
       [47, 54, 61]])

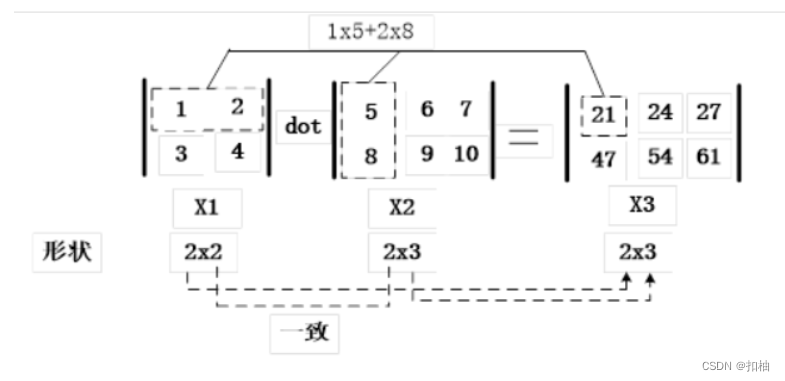
图2展示了点乘（矩阵乘法）的逻辑

下面用虚线框住的矩阵里面的东西，代表下面：
左边矩阵第一行，和右边矩阵第一列，逐个相乘再求和，得到输出矩阵的第一行第一列上的单个元素。

左边矩阵的列轴的大小，必须与右边矩阵的行轴的大小相等。

图2

第2部分：统计函数

NumPy内置的统计函数可以简化数据分析的工作。

c = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])

print("平均值：", np.mean(c))
print("中位数：", np.median(c))
print("标准差：", np.std(c))
print('最大值', np.max(c))
print('最小值', np.min(c))

这段代码会输出数组的平均值、中位数、标准差、最大值和最小值。

第3部分：广播机制

NumPy的广播机制允许对不同形状的数组进行数学运算。这是NumPy强大的功能之一，但也是比较抽象的概念。

简单来说，广播机制会按照一定的规则扩展数组的形状，使其匹配，然后进行运算。

通过代码案例感受广播

下面代码的广播机制的逻辑将会展示在下面的图中。

A = np.arange(0, 40,10).reshape(4, 1)
B = np.arange(0, 3)

C = A + B

输出结果是：

array([[ 0,  1,  2],
       [10, 11, 12],
       [20, 21, 22],
       [30, 31, 32]])

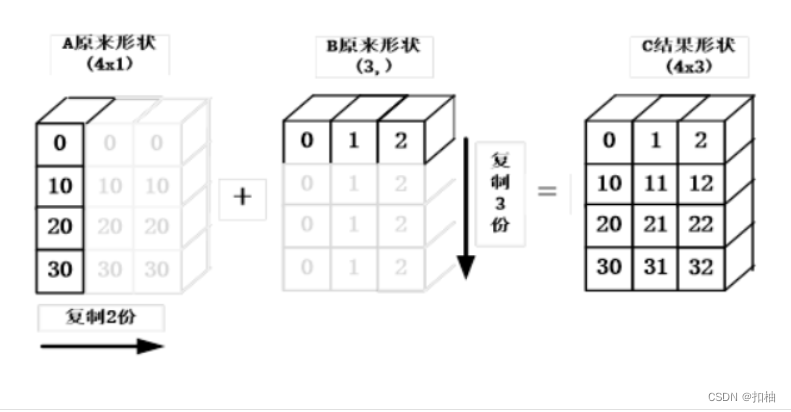
对于上面的代码的广播机制，请看下图：

图3

广播机制的具体规则

广播机制遵循四个基本规则，确保形状不完全匹配的数组也能进行运算。
建议结合更下面的逐条规则剖析刚才的广播代码的文段来理解广播机制的具体规则。

NumPy的通用函数中，要求输入的数组形状，也就是shape属性是一致的，当数组的shape不相等的时候，则会使用广播机制。调整数组使得shape一样，不过，需满足一定规则，否则将出错。这些规则可归结为以下四条：

1. 让所有输入数组都向其中shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐；如：a：2x3x2；b：3x2；则b向a看齐，在b的前面加1：变为：1x3x2
2. 输出数组的shape是输入数组shape的各个轴上的最大值；
3. 如果输入数组的某个轴和输出数组（由参与计算的数组中的各个轴的最大值组成，请看规则2）的对应轴的长度相同或者其长度为1时，这个数组能够用来计算，否则出错；
4. 当输入数组的某个轴的长度为1时，沿着此轴运算时都用此轴上的仅有的一组值进行计算。

逐条规则剖析刚才的广播代码

我们刚才讲过的广播机制的代码如下所示：

A = np.arange(0, 40,10).reshape(4, 1)
B = np.arange(0, 3)

C = A + B

输出结果是：

array([[ 0,  1,  2],
       [10, 11, 12],
       [20, 21, 22],
       [30, 31, 32]])

1. 满足规则1：数组A的shape为(4,1)，有4行1列，数组B的shape为(3,)，加1补齐后，即有1行3列。
2. 满足规则2：C是输出数组，它的形状是输入数组的各个轴上的最大值，数组A拥有最大的行轴，有4行；数组B只有一行，但是有3列，这是最大的列轴。
3. 满足规则3：输出数组为C，shape为(4, 3)，对于shape为(4, 1)的数组A，行轴大小刚好与数组C相等，列轴大小为1，数组B同理。
4. 满足规则4：如上面的图3所示。