机器学习实战—集成学习
文章目录
一.简介
1.1 集成学习
一群人的智慧总是比一个人强,这就是集成学习的核心思想。如果你聚合一组预测器(比如分类器或回归器)的预测,得到的预测结果也比最好的单个预测器要好。这样的一组预测器称为集成,这种技术也叫集成学习。
1.2 随机森林
我们训练一组决策树分类器,每一棵树都基于训练集不同的随机子集进行训练。做出预测时,只需要获得所有树各自的预测,然后得票最多的类别作为预测结果。这样一组决策树的集成被称为随机森林,随机森林是迄今可用的最强大的机器学习算法之一。
二.集成学习—投票分类器
2.1 概念
如果我们已经训练好了一些分类器,并且每个分类器的准确率都比较客观,为了创建一个更好的分类器,最简单的方法就是聚合每个分类器的预测,然后将的票最多的结果作为预测类别。这种大多数投票分类器称为硬投票分类器。事实上,即使每个分类器都是弱学习器(意味着它的的预测效果只比随机预测好一点),通过集成依然可以实现一个强学习器
当预测器尽可能相互独立时,集成方法的效果最优。获得多种分类器的方法之一就是使用不同的算法进行训练(例如逻辑回归、SVM、Knn等)。这会增加它们犯不同类型错误的机会,从而提高集成的准确率。
2.2 代码实现
使用到了随机森林、SVM和逻辑回归来集成一个投票分类器
from sklearn.ensemble import RandomForestClassifier #随机森林分类器
from sklearn.ensemble import VotingClassifier #投票分类器
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
iris=load_iris() #加载数据集
X_train, X_test, Y_train, Y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=42)
log_clf=LogisticRegression() #逻辑回归评估
rnd_clf=RandomForestClassifier()
svm_clf=SVC()
voting_clf=VotingClassifier(
estimators=[('lr',log_clf),('rf',rnd_clf),('svc',svm_clf)],
voting='hard' #硬投票#
)
voting_clf.fit(X_train,Y_train)
print(clf.__class__.__name__,accuracy_score(Y_test,voting_clf.predict(X_test)))
结果输出为预测准确率(预测全对为1)

如果voting='hard’表示为voting='soft’这时候我们的硬投票分类器就变成了软投票分类器,从前面我们知道硬投票分类器是选择具有最高票数类的集合(如果有三个投票器中有两个认为当前水果是苹果,一个认为是橘子,则苹果的票最多所以硬投票法会认为当前水果是苹果),而软投票分类器下每个分类器会计算出类别的概率,然后将概率在所有单分类器上平均,最后选出平均概率最高的类作为预测(同样我们有两个个分类器,分类器 1 以 40% 的概率预测对象是一块苹果,而分类器2 以 60% 的概率预测它是一个苹果,那么软投票分类器会认为有(40%+60%)/2=50%的概率认为这个水果上苹果,最后软投票器会选择平均概率最高的类别)
三.集成学习—bagging和pasting
3.1 简介
前面介绍投票分类器时我们获得不同分类器来集成学习的第一种方法,即直接使用不同的算法。现在介绍的另一种思想就是对于每个预测器都使用相同的机器学习算法,但是在不同的训练集的子集上训练(注意子集的选择上随机的)。在对于子集的不同的选取方式(下面我们会称为抽样方式)的不同,我们可以将抽样方式分为两种类型:
- bagging方法(bootstrap aggregating),也叫做自举汇聚法,采样时样本放回(即原训练集不会发生变化),下一个预测器继续抽样
- pasting方法,采样时样本不放回(即原训练集变小了),下一个预测器继续抽样
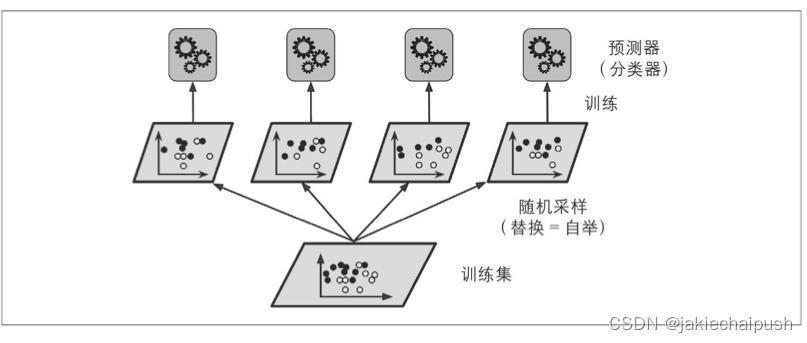
采用bagging和pasting方法,没可以通过不同的CPU内核甚至不同的服务器并行地训练预测器,类似的预测同样也是可以并行的,这就是bagging和pasting方法如此流行的原因,它是非常易于扩展的。
3.2 Scikit-Learn中使用bagging和pasting
下面使用了BaggingClassifier类解决分类问题,预测器使用的机器学习算法是决策树算法
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf=BaggingClassifier(DecisionTreeClassifier(),n_estimators=500,max_samples=100,bootstrap=True,n_jobs=-1)
bag_clf.fit(X_train,Y_train)
y_pred=bag_clf.predict(X_test)
n_estimators=500:表示有500个决策树分类器
max_samples=100:表示每次从训练实例中选取100个实例进行训练
如果基本的预测器都可以估计类别预测(即有predict_proba()方法),则BaggingClassifier会自动使用软投票机制(如果要使用pasting,则将bootstrap=false就行)
3.3 包外评估
- 简介
对于bagging采样方法,我们每次采样都会将样本放回原来的训练集,所以对于每个预测器抽样基于训练集的大小都是一样的,如果我们每次采样的比例假如我们都只采用60%,那么对于每个预测器都会剩下40%的实例没有使用到,这样的实例我们称为包外实例(oob),因此我们可以直接将每个预测器模型在这没使用到的40%的数据上进行评估,而无需再单独的区设置验证集来进行评估,这种思想我们就叫做包外评估。
- API使用
在Scikit-Learn中,我们创建BaggingClassfier时,设置oob_score=TRUE我们就可以使用包外评估了
from sklearn.metrics import accuracy_score
bag_clf=BaggingClassifier(DecisionTreeClassifier(),n_estimators=500,bootstrap=True,n_jobs=1,oob_score=True)
bag_clf.fit(X_train,Y_train)
y_pred=bag_clf.predict(X_test)
accuracy_score(Y_test,y_pred)
3.4 随机补丁和随机子空间
BaggingClassifier类也支持对特征进行采样(针对实例的特定的某个或某些特征进行采样),采用由两个超参数控制:max_features和bootstrap_features,由于是特征采样,因此每个预测器将用输入特征的子集(随机的)进行训练。
- 随机补丁方法:对训练实例和特征都进行采样(只选取一部分实例的部分特征)
- 随机子空间法:保留所哟的训练实例但对特征进行抽样(选取所有实例的部分特征)
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
X_train, X_test, Y_train, Y_test = train_test_split(iris.data[:,2:], iris.target, test_size=0.3, random_state=42)
bag_clf=BaggingClassifier(DecisionTreeClassifier(),n_estimators=500,max_features=2,
bootstrap_features=iris.feature_names[2:],bootstrap=True,n_jobs=-1)
bag_clf.fit(X_train,Y_train)
y_pred=bag_clf.predict(X_test)
四.集成学习—随机森林
4.1 简介
前面已经介绍过随机森林就是一群决策树的集成,因此我们可以将随机森林理解为一种特殊的集成学习,(决策树看我这篇博客)。由于是一种集成学习,所以随机森林应该也也有着很多的随机性,在决策树中我们通过不纯度来选择决策边界来分裂节点,但在随机森林中我们分裂节点的方法发生了些许变化,随机森林中的决策树是在随机生成的特征子集里搜索最好的特征,这样随机森林在决策树的生长上有了更多的随机性和多样性,这里用更高的偏差换取了更低的方差(偏差是算法在训练集上的错误率,方差上算法在测试集上的错误率,由于随机森林使得决策树的生长更加随机,所以它对训练数据可能拟合的效果没那么好的,导致偏差上升,但由于其随机性增强这就导致它对测试数据拟合的更好,这就是所谓的方差下降)
4.2 API使用
这里使用的是Scikit-Learn提供的RandomForestClassifier接口
from sklearn.ensemble import RandomForestClassifier
rnd_clf=RandomForestClassifier(n_estimators=500,max_leaf_nodes=16,n_jobs=-1)#n_jobs表示并行的意思,多余决策树之间并行运行
rnd_clf.fit(X_train,Y_train)
上面的代码使用所有的可用的CPU内核(n_jobs=-1),训练了一个拥有500棵树的随机森林分类器(每棵树限制为最多16个椰子树节点)
4.3 极端随机树
在上面我们说到随机树里单棵决策树的生长过程中每个节点的分裂时是选取的随机特征子集中最好的一个特征,如果我们在随机的特征子集中选择的不再是最好的特征而是随机选择一个,这样决策树的增长会更加的随机,这种极端随机的决策树组成的森林称为极端随机树集成。子啊scikit-Learn中使用ExtraTreesClassifier类可以创建一个极端随机树分类器,它的使用方法和RandomForestClassifier的使用方法是一样的。
4.4 特征重要性
在决策树中我们使用CART剪枝训练算法来选择特征设定阈值,而被选择的节点相比于那些没有被选择的节点上更加重要的。而在随机森林中使得测量每个特征的相对重要性变得更加容易,Scikit-Learn通过查看使用该特征的树节点平均减少不纯度(为了要将表格转化为一棵树,决策树需要找出最佳结点和最佳的分枝方法,对分类树来说,衡量这个“最佳”的指标叫做“不纯度”。通常来说,不纯度越低,决策树对训练集的拟合越好)的程度来衡量该特征的重要性,也就是减少的不纯度越多就越重要。
from sklearn.datasets import load_iris
iris=load_iris()
rnd_clf=RandomForestClassifier(n_estimators=500,n_jobs=-1)
rnd_clf.fit(iris["data"],iris["target"])
for name ,score in zip(iris["feature_names"],rnd_clf.feature_importances_):
print(name,score)
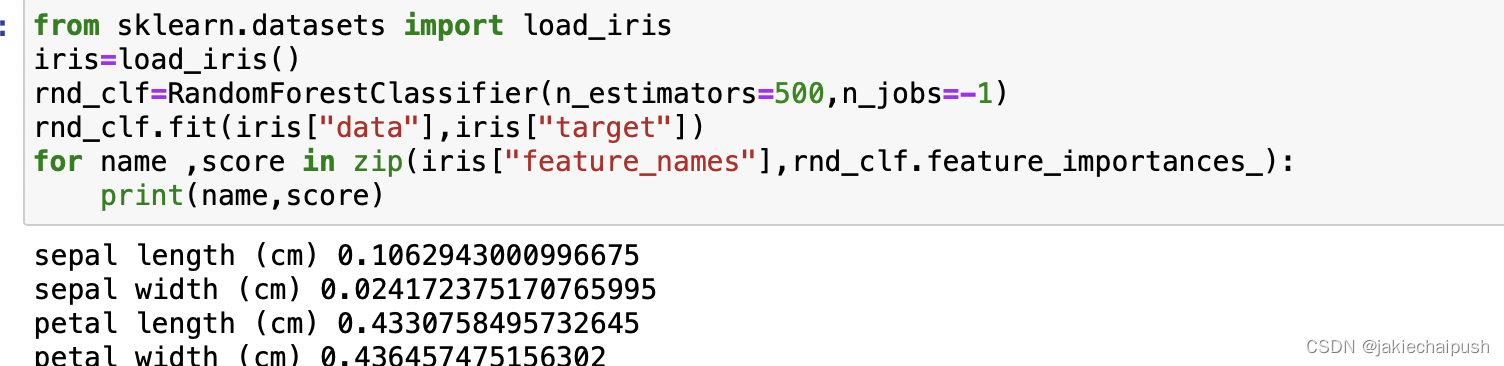
代码中我们通过rnd_clf.feature_importances_来获取每个特征的重要性,可以看出petal width(cm)是最重要的,并且所有特征重要性分数加起来是1(因为Scikit-learn会在训练后为每个特征自动计算该分数,然后对结果进行缩放以使得所有重要性分数之和为1)
五.集成学习—提升法Boosting
5.1 简介
boosting是指可以将几个弱学习器结合成一个强学习器的任意集成方法。大多数提升法的总体思路是循环训练预测器,每一次都对其前序预测器做出一些改正。
5.2 AdaBoost
AdaBoost是目前最流行的提升法方法,它的思路也是遵循循环训练预测器,新的预测器对其前面的预测器进行纠正的方法之一就是更加关注前序欠拟合的训练实例,这样新的预测器会不断地越来越关注于难缠的问题,这就是AdaBoost技术
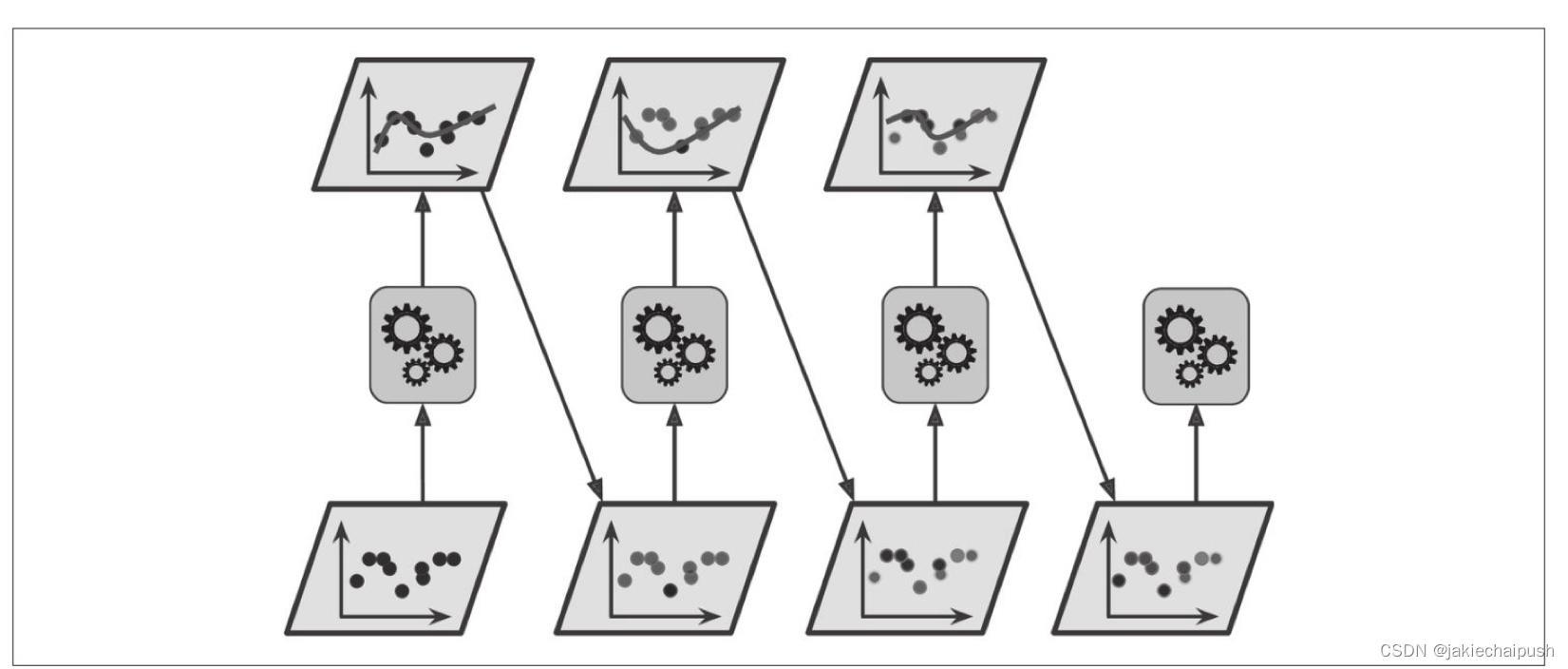
当这种依序学习技术有一个重要的缺陷就是无法并行,因为每个预测器只能在前一个预测器训练完成并评估之后才能开始训练,所以在扩展方面,它的表现不如bagging和pasting方法
5.2 AdaBoost原理解析
- AdaBoost算法的初始时会将每个实例权重
w
(
i
)
w^{(i)}
w(i)最初设置为
1
m
\frac 1 m
m1,然后对第一个预测器进行训练,并根据训练集计算其加权错误率
r
1
r_1
r1,第j个预测器的加权错误率的求法
r j = ∑ i = 1 m w ( i ) ( y ^ j ( i ) ≠ y ( i ) ) ∑ i = 1 m w ( i ) r_j=\frac {\sum_{i=1}^m w^{(i)}(\hat y_j^{(i)}\neq y^{(i)})} {\sum_{i=1}^m w^{(i)}} rj=∑i=1mw(i)∑i=1mw(i)(y^j(i)=y(i))
y ^ j ( i ) \hat y_j^{(i)} y^j(i)是第i个实例的第j个预测器的预测
- 预测器的权重这里我们记为 a j a_j aj,它的计算方法如下列公式所示。其中 β \beta β是我们的学习率超参数(默认为1),可以看出我们的预测器越准确( r j r_j rj越小)其权重就越高。
a j = β l o g 1 − r j r j a_j=\beta log \frac {1-r_j} {r_j} aj=βlogrj1−rj
- 然后AdaBoost算法使用下面公式来更新实例的权重,从而提高了错误分类的实例的权重
对于
i
=
1
,
2
,
.
.
.
.
.
,
m
对于i=1,2,.....,m
对于i=1,2,.....,m
w
(
i
)
←
{
w
(
i
)
,
如果
y
^
j
(
i
)
=
y
(
i
)
w
(
i
)
e
x
p
(
a
j
)
w^{(i)}\leftarrow \begin{cases} w^{(i)},如果 \hat y_j^{(i)}=y^{(i)}\\ w^{(i)}exp(a_j)\\ \end{cases}
w(i)←{w(i),如果y^j(i)=y(i)w(i)exp(aj)
4. 然后对所有实例权重进行归一化(除以
∑
i
=
1
m
w
(
i
)
\sum_{i=1}^m w^{(i)}
∑i=1mw(i))
5. 最后使用更新后的权重训练一个新的预测器,然后重复整个过程(计算新预测器的权重,更新实例权重)直到达到所需的预测器或得到完美的预测器时算法结束
a
1
f
1
+
a
2
f
2
+
.
.
.
+
a
n
f
n
=
F
a_1f_1+a_2f_2+...+a_nf_n=F
a1f1+a2f2+...+anfn=F
a i a_i ai是我们第i个预测器的权值(计算方法如上), f i f_i fi是我们第i个预测器的预测结果
- 最后进行预测,AdaBoost就是简单地计算所有预测器的预测结果,并使用预测器权重 a j a_j aj对他们进行加权,最后得到大多数加权投票的类就是预测器给出的预测类
总结:再看一下AdaBoost算法的思想,其实就是一种“前人栽树,后人乘凉”的思想,通过一次次迭代训练使得预测器越来越强大,在一次次迭代过程中,当前训练的模型只关心前一个训练的模型的错误所在,然后专注于解决这个错误,具体的Adaboost运作流程如下:
- 初始化所有的样本的权重为 w ( i ) = 1 m w^{(i)}=\frac 1 m w(i)=m1
- 然后利用当前预测器的训练结果更新所有的样本的权重(上面的第3步),对于预测正确的样本我们权重保持不变,对于预测错误的样本我们会增加其权重
- 然后基于这个实例权重已经更新的训练集,我们再训练下一个弱预测器(这时会更加关注权重大的样本的,即上一次预测错误的样本的)
- 然后迭代上面过程
- 最后进行预测
5.3 AdaBoost的API使用
Scikitlearn使用的是AdaBoost的多分类版本,叫做SAMME(基于多类指数损失函数的逐步添加模型),如果使用的预测器可以估算出每类的概率,可以使用SAMME的变体,SAMME.R,它和SAMME不同的是,它依赖的是类概率而不是类预测。
from sklearn.ensemble import AdaBoostClassifier
ada_clf=AdaBoostClassifier(DecisionTreeClassifier(max_depth=1),n_estimators=200,algorithm="SAMME.R",learning_rate=0.5)
ada_clf.fit(X_train,Y_train)
上面代码的决策树的深度为1(max_depth=1,即每棵树只有两个叶子节点),创建了200棵这样的决策树(n_estimators=200),使用的算法是SAMME.R(algorithm=“SAMME.R”),学习率 β \beta β为0.5(learning_rate=0.5)。如果出现过拟合问题我们可以从两个方面下手:
- 减少决策树的数量
- 对每个决策树进行正则化
5.4 梯度提升
上面上面介绍的AdaBoost算法,提升法中梯度提升算法也是使用非常广泛的,于AdaBoost的原理一样它也是逐步在集成中添加预测器,并对每一个前序预测器的错误进行改正。不同之处在于,他不像AdaBoost那样在每个迭代中调整实例的权重 w w w,而是让新的预测器针对前预测器的残差进行拟合。(残差在数理统计中是指实际观察值与估计值(拟合值)之间的差)
5.5 梯度提升原理
下面的案例是一个简单的回归问题,来解释梯度提升算法的运作原理,使用决策树作为基础预测器,这被称为梯度树提升或者梯度提升回归树(GBRT)
- 初始:训练集上训练第一个决策树
from sklearn.tree import DecisionTreeClassifier
tree_reg1=DecisionTreeClassifier(max_depth=2)
tree_reg1.fit(X_train,Y_train)
决策树的深度为2
- 第二步:针对第一个预测器的残差训练第二个决策树
y2=Y_train-tree_reg1.predict(X_train) #计算残差
tree_reg2=DecisionTreeRegressor(max_depth=2)
tree_reg2.fit(X_train,y2)
- 第三步:将前面得到的两棵树的预测相加,对性实例进行预测
y_pred=sum(tree.predict(iris.data[2:3,2:]) for tree in(tree_reg1,tree_reg2))
y_pred
以上便是梯度提升的运作原理
5.6 梯度提升API使用
scikit-learn使用的GradientBoostingRegressore类
from sklearn.ensemble import GradientBoostingRegressor
gbrt=GradientBoostingRegressor(max_depth=2,n_estimators=3,learning_rate=1.0)
gbrt.fit(X_train,Y_train)
在这里超参数learning_rate(学习率)对每棵树的贡献进行缩放,其值越小则每棵树的贡献越小,则需要更多的树来拟合训练集,这样同样最后模型的泛化效果会比较好。
总结:介绍完梯度提升我们会发现一个新的问题,就是在使用梯度提升算法时我们如何选择合适的树的数量,这里有两种思路:
- 使用提前停止法(提前停止(英语:early stopping)是一种在使用诸如梯度下降之类的迭代优化方法时,可对抗过拟合的正则化方法)
- 使用XGBoost(其提供了梯度提升的优化实现)