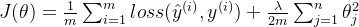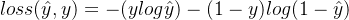【机器学习】正则化

正则化是防止模型过拟合的方法，它通过对模型的权重进行约束来控制模型的复杂度。

正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了数据的噪声，一般不正则化b。

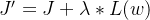
$J'=J+\lambda*L(w)$

正则化分为L1正则化和L2正则化：

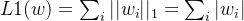
$L1(w)=\sum_i||w_i||_1=\sum_i|w_i|$

L1正则化大概率会使很多参数变为0，因此该方法可通过稀疏参数，即减少参数的数量，降低复杂度。

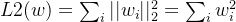
$L2(w)=\sum_i ||w_i||^2_2=\sum_i w_i^2$

L2正则化会使参数很接近但不为零，因此该方法可通过减小参数值的大小降低复杂度。

对于模型权重系数 w 求解是通过最小化目标函数实现的，即求解：

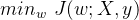
$min_w\ J(w;X,y)$

假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的程序来选择这些惩罚的程度。记：

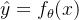
$\hat y=f_\theta(x)$

对线性回归：

$J(\theta)=\frac{1}{2m} \left[\sum\limits^m_{i=1}(\hat y^{(i)}-y^{(i)})^2 + \lambda\sum\limits_{j=1}^{n}\theta_{j}^{2}\right]$

对逻辑回归：

$J(\theta)=\frac 1 m \sum^m_{i=1}loss(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}$

$\\loss(\hat y,y)=-(ylog\hat y)-(1-y)log(1-\hat y)$