【论文简述】GeoNet++: Iterative Geometric Neural Networkwith Edge-Aware Refinement for Joint D(PAMI 2022)
一、论文简述
1. 第一作者:Xiaojuan Qi
2. 发表年份:2022
3. 发表期刊:PAMI
4. 关键词:深度估计,表面法线估计,3D点云,3D几何一致性,3D重建,边缘感知,卷积神经网络(CNN),几何神经网络
5. 探索动机:以前的大多数方法独立执行深度和正态估计,可能导致预测不一致和较差的3D表面重建。预测深度图在平面区域可能会发生畸变。利用表面法线在这些区域不改变的事实可以帮助对平面进行降噪。这促使探索深度和表面法线之间的几何关系。一种可能的设计是建立一个卷积神经网络(CNN)直接从数据中学习这种几何关系。然而实验证明了目前存在的CNN架构(例如,VGG-16)不能从深度预测好的法线。发现训练总是收敛到非常差的局部最小值,即使是经过精心调整的体系结构和超参数。另一个挑战来自池化操作和大的感受野,这使得当前的体系结构在对象边界附近表现不佳。由于边界模糊,红色边界框内的点在3D中是分散的。因此,对于需要障碍物检测和避障的机器人应用来说,这是一个问题。
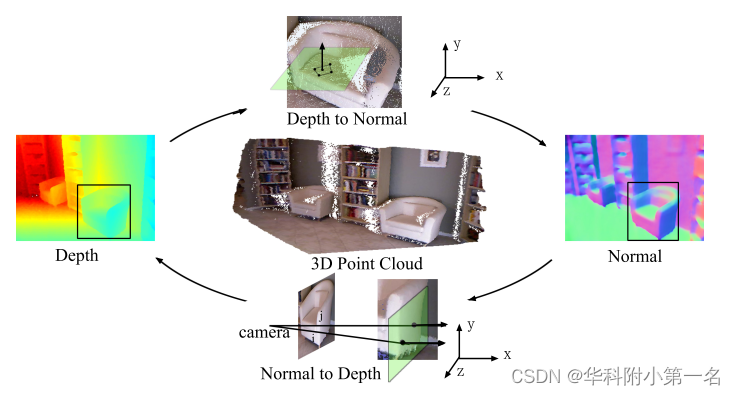
深度和表面法线之间的几何关系。点云是通过针孔相机模型将深度值投射到3D中获得的。通过求解线性方程组,从点云中估计表面法线;深度受到由邻近点及其表面法线确定的局部平面的约束。一方面,表面法线由与三维点的切平面确定,可以从它们的深度估计法线;另一方面,深度受到由表面法线确定的切平面局部表面的约束。
6. 工作目标:上述事实促使设计一种新的架构,明确地结合并执行考虑物体边界的3D几何约束。
7. 核心思想:提出了具有边缘感知细化的几何神经网络(GeoNet++),它将几何约束和边界信息集成到CNN中,用于从单个图像中联合预测深度和表面法线图。
- Building on top of two-stream CNNs, GeoNet++ captures the geometric relationships between depth and surface normals with the proposed depth-to-normal and normal to-depth modules. In particular, the “depth-to-normal” module exploits the least square solution of estimating surface normals from depth to improve their quality, while the “normal-to-depth” module refines the depth map based on the constraints on surface normals through kernel regression. Boundary information is exploited via an edge-aware refinement module.
- GeoNet++ effectively predicts depth and surface normals with strong 3D consistency and sharp boundaries resulting in better reconstructed 3D scenes. Note that GeoNet++ is generic and can be used in other depth/normal prediction frameworks to improve the quality of 3D reconstruction and pixel-wise accuracy of depth and surface normals.
- Furthermore, we propose a new 3D geometric metric (3DGM) for evaluating depth prediction in 3D. In contrast to current metrics that focus on evaluating pixel-wise error/accuracy, 3DGM measures whether the predicted depth can reconstruct high-quality 3D surface normals. This is a more natural metric for many 3D application domains.
8. 实验结果:
Experimental results on NYUD-V2 and KITTI datasets show that our GeoNet++ achieves decent performance, while being more efficient.
9. 论文及代码下载:
https://arxiv.org/abs/2012.06980
https://github.com/xjqi/GeoNet
二、实现过程
1. 整体架构
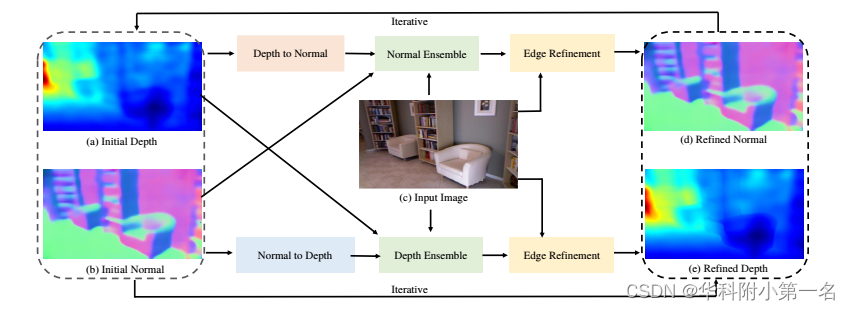
总体架构如图所示。基于主干CNN预测的初始深度图,应用depth-to-normal模块将初始深度图转换为法线图。该模块使用考虑几何约束的初始深度图细化表面法线。类似地,给定初始表面法线估计,使用normal-to-depth模块生成深度。这通过将固有的几何约束纳入法线深度估计来增强深度预测。使用上述组件生成的深度/法线图然后通过深度(法线)集成模块进行调整。此外,通过去除噪声结果并对边界预测进行细化,边缘细化网络进一步改进了预测结果。最后,geonet++可以迭代地应用,将先前迭代的精炼结果作为输入。
2.深度到法线模块
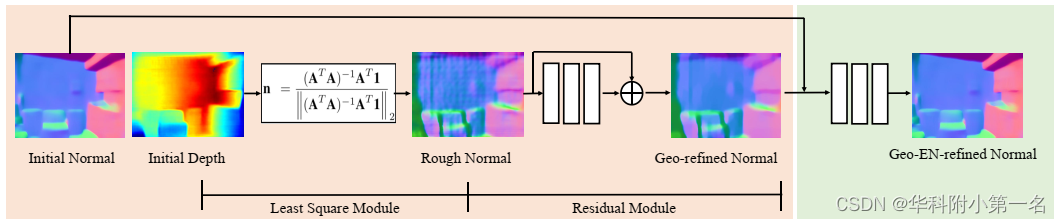
通过直接应用神经网络从深度中学习几何上一致的表面法线是非常困难的。为此,提出了一个深度到法线转换模块,该模块明确地将深度法线一致性整合到深度神经网络中。从最小二乘模块开始讨论,将其视为一个固定权重的神经网络。然后,描述残差子模块,其目的是平滑并将结果与初始法线相结合,如左图所示。
针孔相机模型。作为一种惯例,采用针孔相机模型。(ui, vi)表示为像素i在二维图像中的位置。其在三维空间中的对应位置为(xi, yi, zi),其中zi是深度。基于透视投影的几何原理有
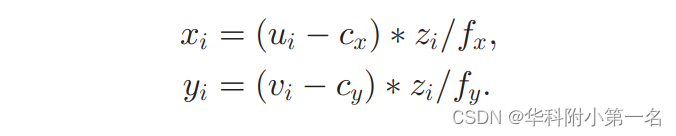
其中fx和fy分别是x和y方向的焦距。cx和cy是焦点的坐标。
最小二乘子模块。将从深度图推断表面法线表述为最小二乘问题。具体来说,对于任意像素i,给定其深度zi,依赖针孔相机模型,从它的二维坐标(ui, vi),首先计算其三维坐标(xi, yi, zi)。为了计算像素i的表面法线,需要确定与3d空间中像素i相交的切平面。遵循传统的假设,即局部邻域内的像素位于同一切平面上。特别地,定义相邻像素的集合,包括像素i本身,为
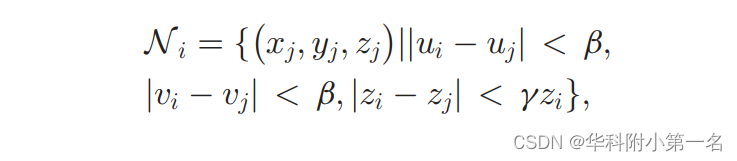
其中β和γ分别是沿x、y和深度轴控制邻域大小的超参数。这些像素在切平面上,表面法线估计n应满足超定线性方程组


b∈K×1是一个常数向量。K是Ni的大小,即相邻点的集合。该问题的最小二乘解使||An−b||2最小,可以用封闭形式计算为:
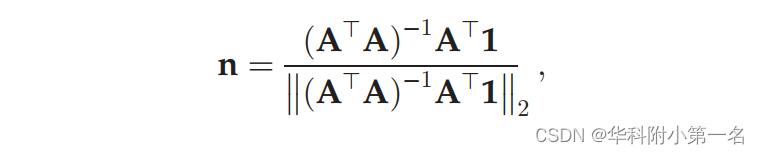
其中1是一个全是1的元素向量。毫不奇怪,上式可以被视为一个固定权重的神经网络,它在给定深度图的情况下预测表面法线。
残差子模块。由于噪声和领域规模不合适等问题。这个最小二乘模块偶尔会产生有噪声的表面法线估计(见图“Rough Normal”)。为了进一步提高质量,提出了一个残差模块,该模块由具有跳跃连接的3层CNN组成。目标是平滑最小二乘模块的噪声估计。
总体结构。深度到法线模块的架构通过明确利用深度和表面法线之间的几何关系,网络规避了前面提到的学习几何上一致的深度和表面法线的困难。请注意,该模块可以与其他从原始图像预测深度图的网络合并并联合微调。
3. 法线到深度模块
对于任意像素i,给定其表面法线(nix, niy, niz)和初步估计的深度zi,目标是完善其深度。首先,注意给定三维点(xi, yi, zi)及其表面法线(nix, niy, niz),可以唯一地确定切平面Pi,它满足下式
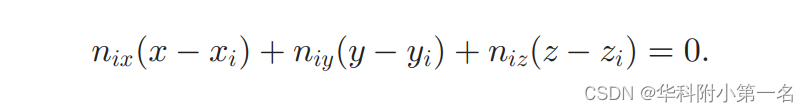
假设i的小邻域内的像素位于切平面Pi上。领域Mi定义为
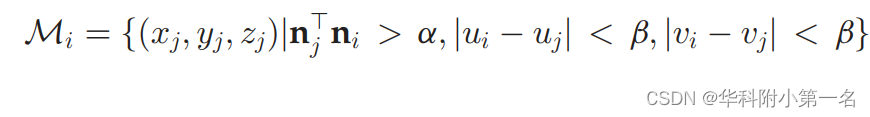
其中β是控制沿x和y轴邻域大小的超参数,α是排除非近似共面空间接近点的阈值,(ui, vi)为二维图像中像素i的坐标。
对于任意像素j∈Mi,如果深度zj给定,我们可以根据方程计算像素i的深度估计为zji
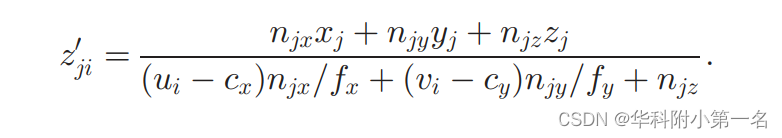
为了细化像素i的深度,使用核回归将邻域中所有像素的估计聚合为
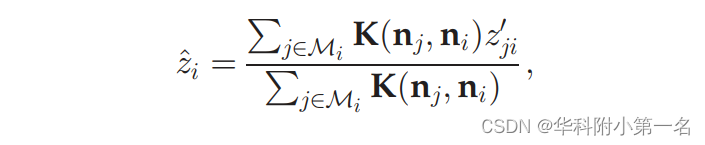
其中z^i是细化深度,ni=(nix, niy, niz),K是核函数。使用线性核(即余弦相似性)来度量ni和nj之间的相似性,即K(nj,ni) =njTni。在这种情况下,法线ni和nj之间的夹角越小,这意味着像素i和j的概率越高在同一切平面上,zji的估计值对z^i的估计值的贡献越大。过程如图4 (b) - (L)所示。

它可以被视为一个投票过程,其中每个像素j∈Mi给出一个“投票”来确定像素i的深度。利用表面法线和深度之间的几何关系,有效地提高了深度估计的质量,而不需要学习任何权重。
4. 深度(法线)集成模块
为进一步提高预测质量,将来自主干网络的“初始深度(法线)”和来自几何细化的“几何细化深度”与图(a)右所示的表面法线和图(b)右所示的深度集成模块结合在一起。下面将详细介绍深度集成模块。法线集成模块共享类似的体系结构。
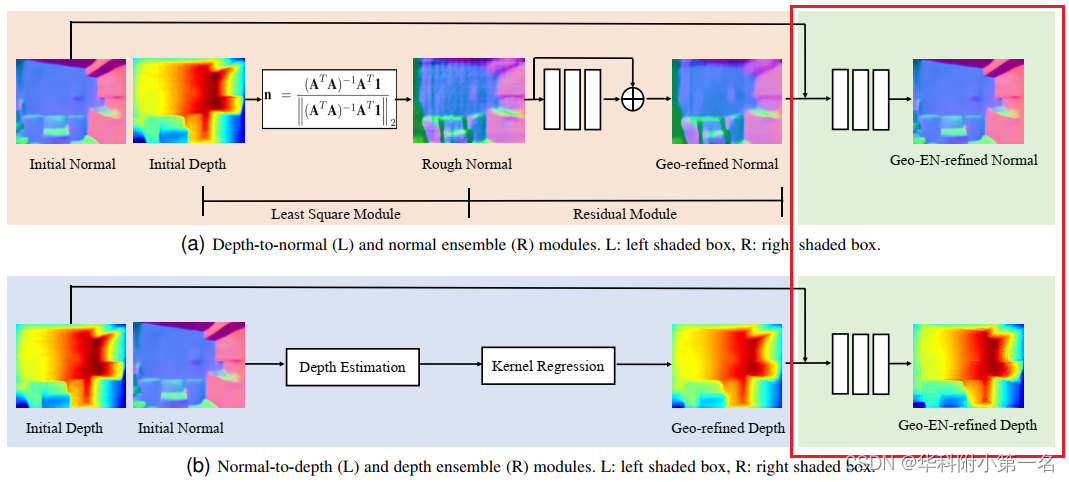
深度集成模块以来自主干网络的“Initial Depth”和来自几何模块的“Geo-refined Depth”作为输入,生成一个精细深度“GeoEN-refined depth”。为了扩大集成模块的感受野,首先对输入进行3个卷积层处理,膨胀率为2,核大小为3 × 3,通道数为128。接下来是另外2个无膨胀卷积层,核大小为3 × 3,通道数为128。
5. 边缘感知细化模块
设计了一个边缘感知的细化模块进一步增强预测。该模块通过逐渐聚集相邻像素的信息来增强边界预测并去除噪声预测。这一过程由一组学习到的权重图(如图所示Weight Maps)来指导。边缘感知细化包含两个子模块,即权重图预测器和递归传播器。该模块对深度和法线预测使用相同的架构,只详细说明深度的细节。
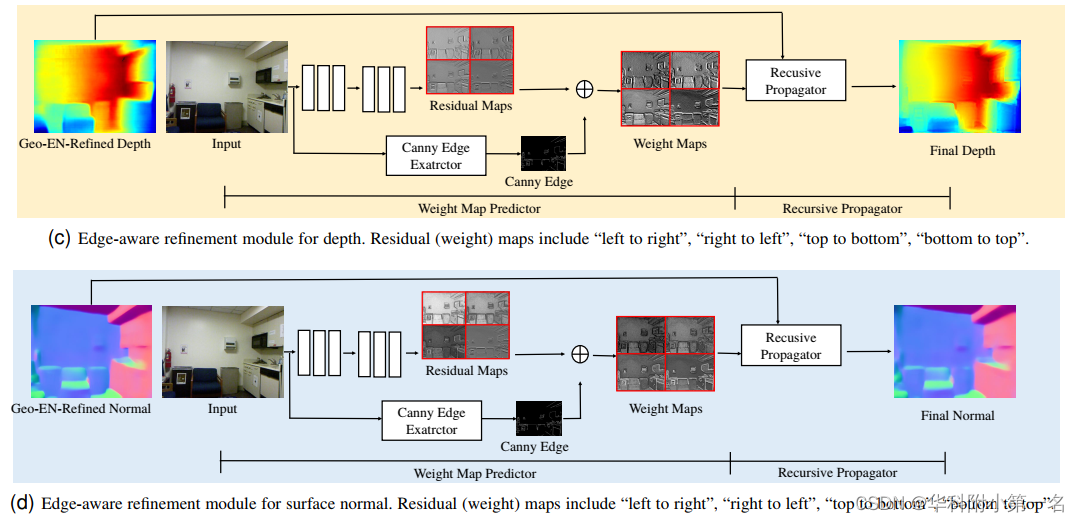
权重图预测器。权重图预测器包含一个提取低级边缘信息的canny边缘算子和一个学习边缘感知的传播权重的残差网络。输出通过元素求和进行融合,如图所示。残差网络包含3个卷积层,具有ReLU非线性,膨胀率为2,核大小为3 × 3,通道数32,然后是3个不扩展的卷积层,使用与上述相同的参数设置。最后,采用核大小为1 × 1、通道数为4的卷积层生成边缘权重图w∈H×W×4,其中H和W为图像空间大小,4个通道表示从左到右(L→R)、从右到左(R→L)、从上到下(T→B)、从下到上(B→T)四个方向的传播权值。用于深度细化的学习到的边缘权重图如图所示。表面法线的相应图如图所示,其中值越大意味着越有可能靠近边界。
递归传播器。递归传播器将边缘权重图W和输入信号X(在例子中是深度或法线图)作为输入,并通过应用以下操作递归地对输入信号进行T次细化
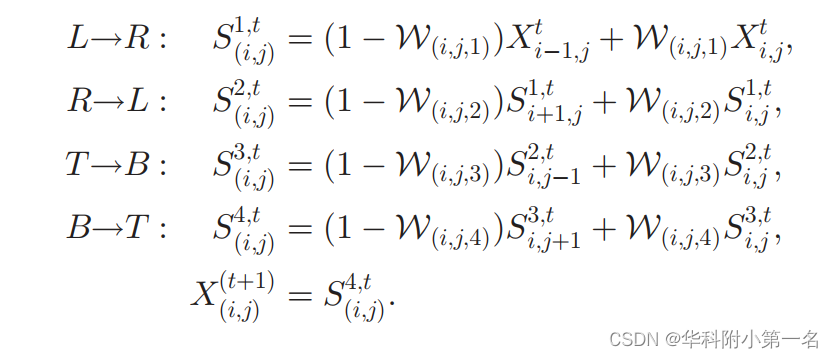
其中,X0=X。S1,t, S2,t, S3,t, S4,t表示在分别步长t次传播的“L→R”、“R→L”、“T→B”和“B→T”之后的中间结果。
在每一步,递归传播器将之前的迭代结果Xt作为输入,并采用从邻近像素和当前深度值扩散的深度加权求和产生一个新的估计Xt+1。权值由学习到的边缘感知权重图W确定。在边界附近的区域,为了避免模糊和保持清晰的结果,学习到的权值Wi,j较大。另一方面,在去除噪声预测的非边界区域,学习到的权重很小。边缘感知权重使能够将计算密集型二维传播分离为四个一维传播,这样在不牺牲质量的情况下效率更高。上面的传播过程执行了T次,以合并远程依赖关系。在实验中使用T=3。
6. 迭代推理和训练细节
迭代推理。可以迭代应用GeoNet++进一步改进结果。以前迭代的改进后的深度和法线图可以进一步作为GeoNet++的输入进行迭代细化。请注意,只在推理期间迭代地应用它。在训练阶段,
GeoNet++只应用一次,减少内存消耗,提高训练效率。
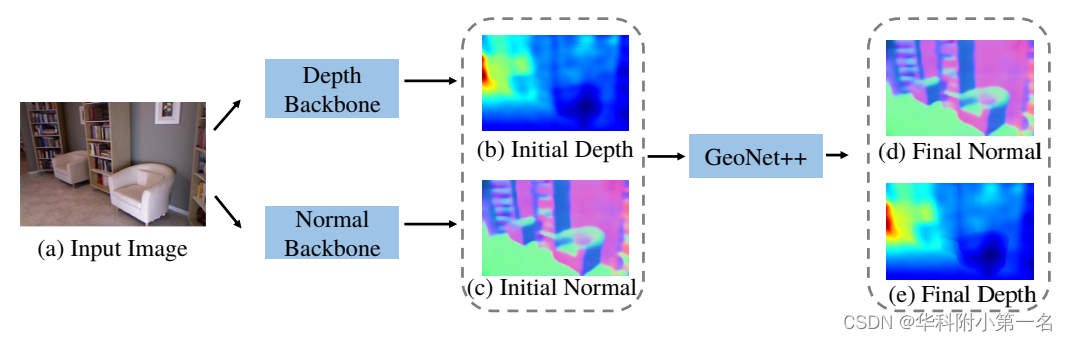
端到端网络训练。完整的系统显示在如图所示。主干网络生成初始深度图和表面法线图,并用GeoNet++结合几何约束和边缘信息对其进行进一步细化。整个系统可以端到端进行训练。在下面,解释训练整个系统的损失函数。将像素i的初始深度、改进深度和真实深度分别表示为zi、z^i和zigt。同样,分别用ni、n^i和ngt i表示初始、改进和真实表面法线。总的损失函数是两个损失的总和,一个是深度损失,一个是法线损失,L = ldepth + lnormal。深度损失表示为
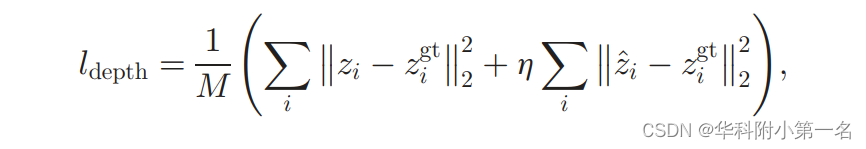
M为总像素数。表面法线损耗为
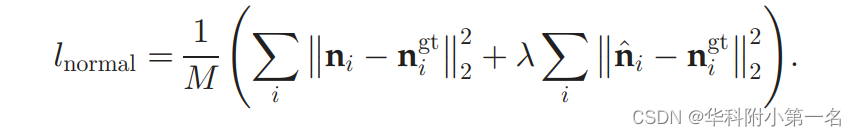
这里λ和η是超参数,平衡了单个项的贡献。