【数据结构】快速排序,基数排序/桶排序
基数排列
:
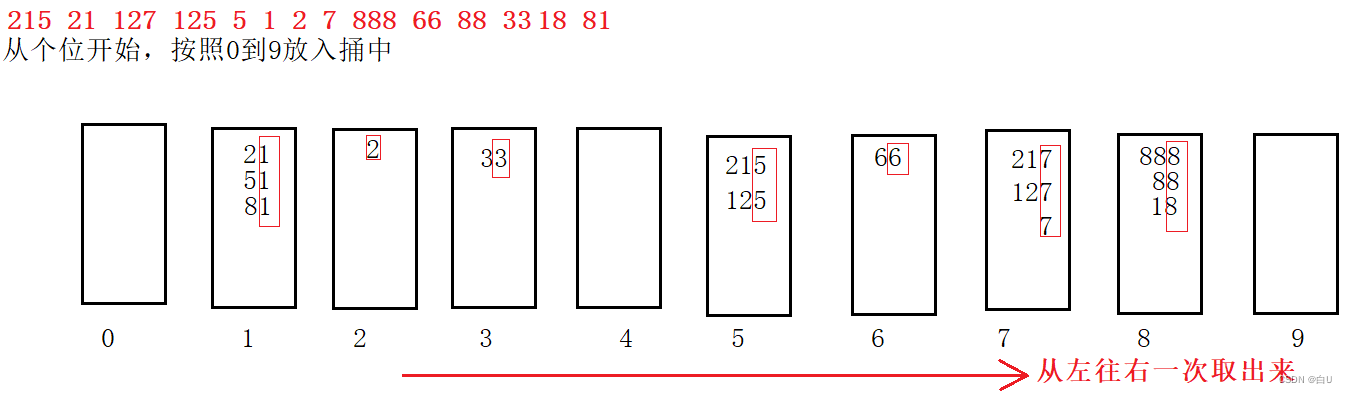
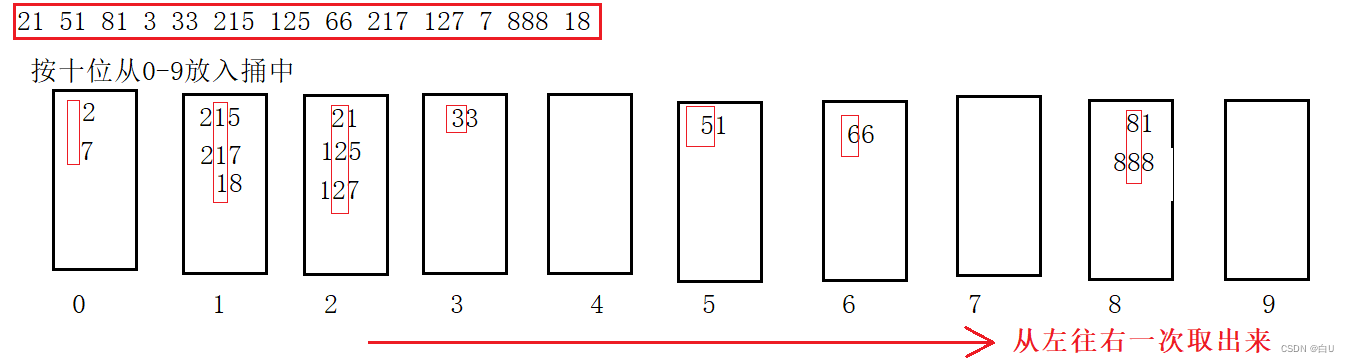
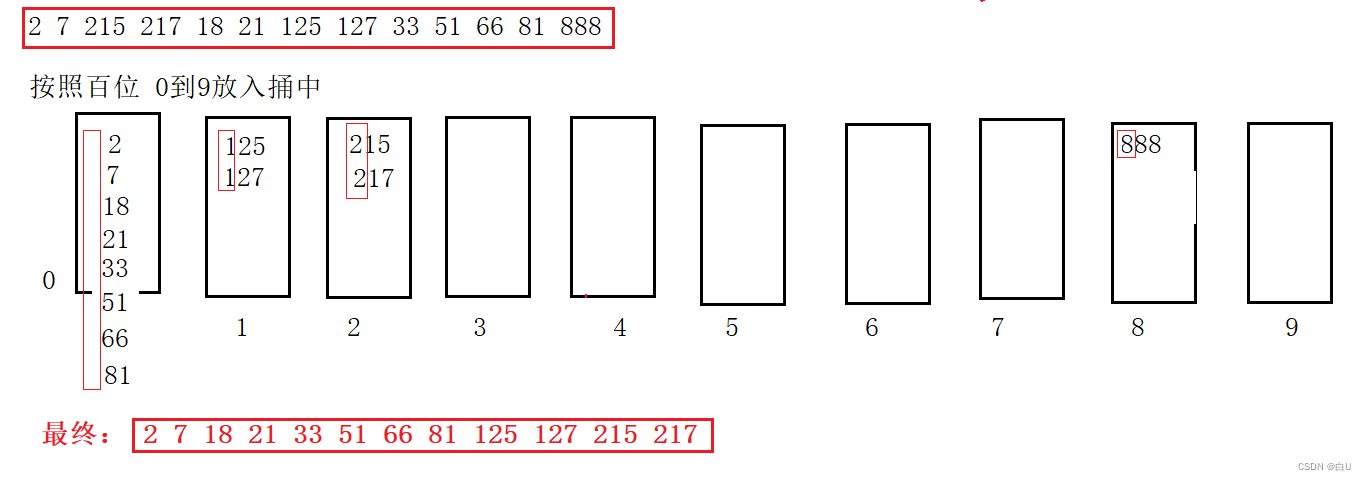
桶排序:低位优先,所有数据从(个位)开始
依次放入10个桶内(入队,再从桶里取出,直到完全有序)。
基数(桶)排序:低位优先,所有数据从低(个)位开始,依次放到对应的桶内(入队),再接着从桶内取出(出队),直到完全有序 时间复杂度O(dn) 空间复杂度O(n) 稳定吗
如下图:
循环的次数和最大值的位数有关
《二维数组实现桶排序》
Get_figure(arr, len); :获取最大值的位数,来作为循环遍历位数的条件
Radix(arr, len, i);:进行将所有数据,按照位数放入桶中,放完之后,再取出来放到arr数组中
Get_Num(arr[i], fin):获取当前位数所在桶的序号。index获取
static int Get_figure(int* arr, int len)
{
//assert
//获取最大值是多少
int tmp = 0;
for (int i = 0; i < len; i++)
{
if (tmp < arr[i])
{
tmp = arr[i];
}
}
//获取tmp的位数
int count = 0;
while (tmp != 0)
{
count++;
tmp = tmp/10; //每次丢掉一个位,直到商变为0
}
//while结束,得到的是最大值的位数count
return count;
}
以fin的规则取n对应的值
static int Get_Num(int arr, int fin)
{
for (int i = 0; i < fin; i++)
{
arr /= 10;//扔掉最低位,获得当前数歌舞ie,示威,百位的数字,
//入249 个位9,十位4,百位2
}
return arr % 10; //得到当前述的最低位
}
以fin位排序一次,放到桶内,再从桶内取出。
static void Radix(int* arr, int len, int fin)
{
int brr[10][20] = { 0 };//十个桶,每个桶初始容量20
int num[10] = { 0 }; //保存每个桶的有效值个数
for(int i = 0;i<len;i++)
{
int index = Get_Num(arr[i], fin);//index就是几号桶
brr[index][num[index]]= arr[i];
//num就相当于要插入的下标
num[index] ++;//对应的桶内数据个数++
}
此时for结束,代表数据全部放入桶内
接着,从0号桶一次取出数据
int k = 0;
for(int i = 0; i <= 9;i++)//i保存了桶号
{
//int k = 0;如果写在着,会导致第二个桶开始所有的数据,每次都收覆盖前一个桶
//保存向arr中存放的空间下标
for (int j = 0; j < num[i]; j++)//从桶内0号下标开始取值,直到取完
{
arr[k++] = brr[i][j];
}
}
}
void RadixSort(int arr[], int len)
{
循环次数,最大值的位数来控制
int count = Get_figure(arr, len);
for (int i = 0; i < count; i++)
{
Radix(arr, len, i);
}
}
《链式队列实现桶排序》
核心代码:
static void LRadix(int* arr, int len, int fin)
{
Head Arr_queue[10];
for(int i = 0;i<10;i++)
{
Init_Iqueue(&Arr_queue[i]);
}
//十个链式队列初始化完成。
for (int i = 0; i < len; i++)
{
int index = Get_num(arr[i], fin);
push(&Arr_queue[index], arr[i]);
}
int k = 0;
for (int i = 0; i < 10; i++)
{
while (!IsEmpty(&Arr_queue[i]))
{
int tmp = 0;
pop(&Arr_queue[i], &tmp);
arr[k++] = tmp;
//可以合并
}
}
}
链式队列实现基数排序和二维数组实现基数排序的区别?

快速排序
快速排序(递归):(越乱越有序)从右向左找比基准值小的,向左放,再从左向右找比基准值大的,向右放,重复此过程 直到完全有序 时间复杂度O(nlogn) 空间复杂度O(logn) 不稳定
优化:
1.如果right-left特别小,直接用冒泡
2.三位取中法,取第一个值,中间值,和最后一个值判断一下,找一不大不小的值作为基准值
不论不大不小的值是哪一个,都将该值和最左边的值交换,再进行下面的操作
3.第三个优化:主要针对快排已经有序,越有序,越慢。
已经完全有序,在执行就会变成选择排序,为了防止这种情况发生,可以自己去打乱一下。
划分函数
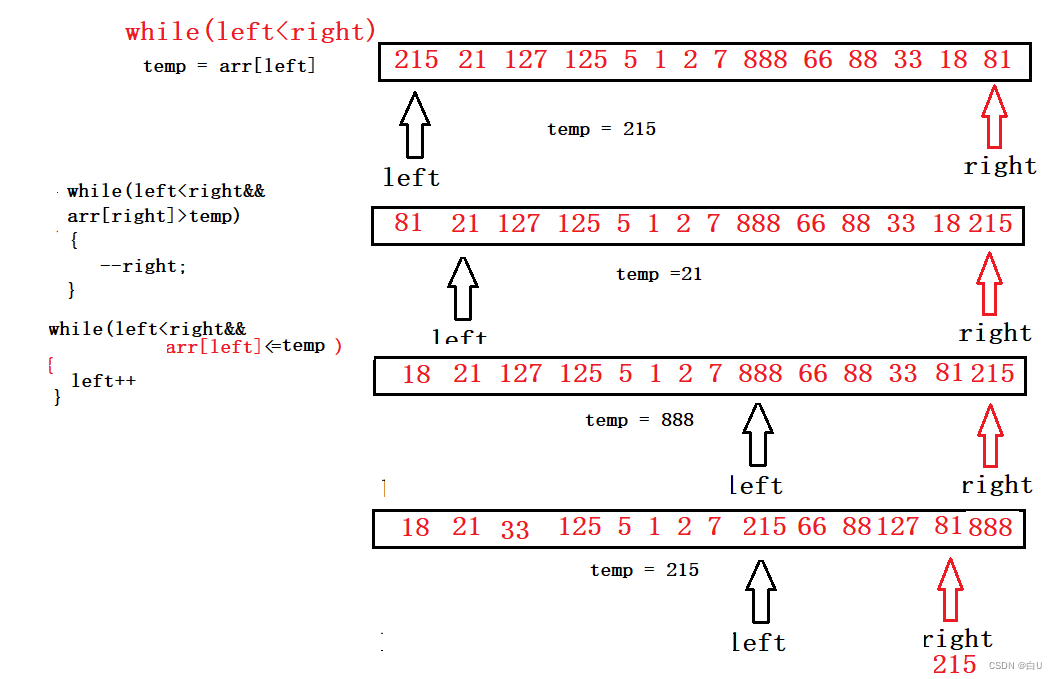

int Partion(int* arr, int left, int right)
{
//将左边第一个数当作基准点
int temp = arr[left];
while (left < right)
{ //基准点在左边,所以从右边开始
while (left < right && arr[right] > temp)//不能等于
{ //从右往左,找比tmp大的,如果小于tmp就把当前值放到左边
--right;
}
if (left < right) arr[left] = arr[right];
while (left < right && arr[left] <= temp)
{ //从左往右找比temp小的,如果比tmp大,就放到右边
++left;
}
if (left < right) arr[right] = arr[left];
}
arr[left] = temp; //arr[right] 也对,因为此时 right=left
return left;//将基准值返回。
}
void SortPass(int* arr, int left, int right)
{
//优化:
//1.如果right-left特别小,直接用冒泡
//2.三位取中法,取第一个值,中间值,和最后一个值判断一下,找一不大不小的值作为基准值
// 不论不大不小的值是哪一个,都将该值和最左边的值交换,再进行下面的操作
//第三个优化:主要针对快排已经有序,越有序,越慢。
//已经完全有序,在执行就会变成选择排序,为了防止这种情况发生,可以自己去打乱一下。
int par = Partion(arr, left, right); //得到第一次划分的基准值下标
if(left < right)
{
if (left < par - 1) //按照基准数分成两边,par是当前左边的下边界
//是右边的始边界
//保证基准值左右两边至少有两个数据
{
SortPass(arr, left, par - 1);
}
if (right > par + 1)
{
SortPass(arr, par + 1, right);
}
}
}
void QuickSort(int *arr,int len)
{
for (int i = 0; i < len - 1; i++)
{
SortPass(arr, 0, len - 1);
}
}