图的连通性问题及Tarjan算法

推荐观看视频教程

一、图的连通性

1. 无向图的连通性

在无向图G＝（V，E）中：

①连通：若节点u和v能够互相到达，则称u,v是连通的；

②连通图：若图中任何节点之间都是可互相到达的，则称G是连通图，否则称G是非连通图；

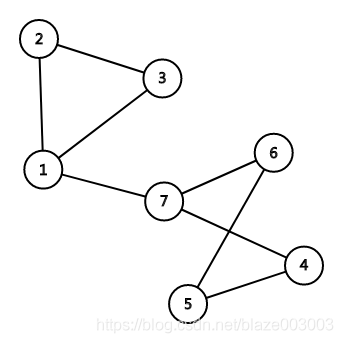这是一个连通图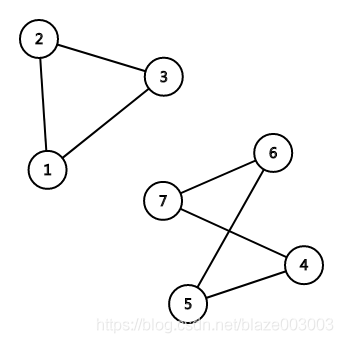这不是一个连通图，

③连通分量（连通分支）：我们可以看出上面右图有两个部分连通的图，叫做连通分量（或连通分支）

④无向图的连通性判定：并查集、DFS、BFS、WARSHALL 算法；

⑤非连通的无向图求连通分量：可通过额外设置计数器count（初始值0）统计出图的连通分量，每调用dfs（或bfs）遍历一次，计数器count增1。当遍历完无向图时，若count=1，则图连通，若count>1，图非连通，count的值就是该图的连通分量数。

需要注意的是，连通分量的提出是以"整个无向图不是连通图"为前提的，因为如果无向图是连通图，则其无法分解出多个最大连通子图，因为图中所有的顶点之间都是连通的。

2.有向图的连通性

①强连通：在有向图中，若节点 u 和节点 v 能互相到达（不必是同一路径），则称 u,v 强连通；

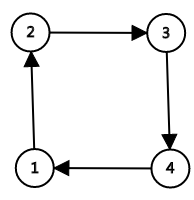节点1可以通过（1，2，3）到达3，节点3可以通过（3，4，1）到达1，所以3和1是强连通；

②强连通图：在有向图 G=(V,E) 中，若对于V 中任意两个不同的顶点 u 和 v，都存在从 u 到 v 以及从 v 到 u 的路径，则称 G是强连通图。

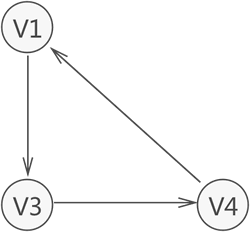这是一个强连通图

③强连通分量SCC(strongly connected components)：非强连通图的极大强连通子图，称为强连通分量。强连通图只有一个强连通分量，即是其自身；非强连通的有向图有多个强连分量。

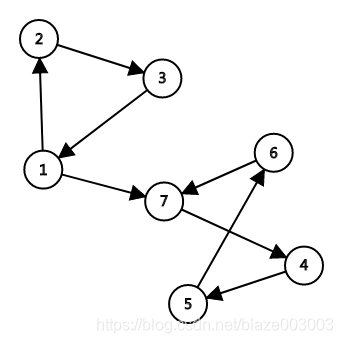这个有向图中有两个强连通分量（2，3，1）和（7，6，4，5）。

小提示：“连通图” 是在无向图 的基础上对图中顶点之间的连通做了更高的要求，而“强连通图” 是在有向图 的基础上对图中顶点的连通做了更高的要求。

④有向图的连通性判定算法：

方法一:可以调用DFS搜索 V 次，V是顶点的个数，就是对每个顶点都做一次DFS搜索，判断是否可达。这样的复杂度为O(V*(V+E))。

方法二:可以参考求解连通分量的算法Tarjan算法，我们可以在O(V+E) 的时间内找到所有的连通分量，如果连通分量的个数为1，则说明该图是强连通的。

⑤有向图求强连通分量算法：Kosaraju 算法和Tarjan算法

二、Tarjan算法

Tarjan（音译为塔扬）算法的核心其实是dfs，主要是通过维护两个数组来完成强连通分量的计算：

dfn[]数组：负责记录每个节点的dfs顺序（简称为dfs序）。

low[]数组：负责记录从每个节点的出发沿可行边所能到达的点中dfs序号最小的序号。

第一个数组好理解：

对于下面左图的有向图进行dfs，并产生dfs序应该是右边的结果

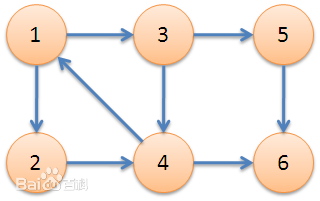
第二个数组费解一点：

 

P2863 [USACO06JAN]牛的舞会

//P2863 [USACO06JAN]牛的舞会The Cow Prom
#include <cstdio>
#include <stack>
using namespace std;
const int maxn=10005;
const int maxm=50005;
struct Edge{
	int v,w,nxt;
}edge[maxm];
int n,m,cnt=1,head[maxn],instack[maxn];
int scctot;
int index;
int dfn[maxn];///节点的dfs序 
int low[maxn];///dfs时，节点能到达的最小dfs序 
int scc[maxn];///每个节点所属的强连通分量 
int num[maxn];///记录每个强连通分量中节点个数 
stack<int>s;
inline void adedge(int u,int v,int w)
{
	edge[++cnt].v=v,edge[cnt].w=w,edge[cnt].nxt=head[u],head[u]=cnt;
}
void tarjan(int u)
{
	if (dfn[u])return;
	index++;
	dfn[u]=low[u]=index;
	instack[u]=1;
	s.push(u);
	for (int i=head[u];i;i=edge[i].nxt)
	{
		int v=edge[i].v;
		if (!dfn[v])///如果没有dfs过，则继续深搜 
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
			///dfs返回后更新当前节点的low值等于当前节点能到达的节点中low值最小的low值 
		}
		if (instack[v])
		///如果v的dfs序已存在，说明从节点u可以回到dfs序更小的节点，或者说已形成了一个环 
		{			
			low[u]=min(low[u],dfn[v]);
			///当前节点u的low值应该等于当前节点能到达的节点中low值最小的low值
		}		
	}
	if (dfn[u]==low[u])///找到一个强连通分量
	{
		scctot++;///强连通分量个数加1 
		while(1)
		{
			int t=s.top();
			scc[t]=scctot;
			num[scctot]++; 
			instack[t]=0;
			s.pop();
			if (t==u)break;
		}
	} 
}
int main()
{
	scanf("%d %d",&n,&m);
	for (int i=1,u,v;i<=m;++i)
	{
		scanf("%d %d",&u,&v);
		adedge(u,v,1);
	}
	for (int i=1;i<=n;++i)
	{
		if (!scc[i])tarjan(i);///如果有节点没有生成所属强连通分量值 
		//if (!dfn[i])tarjan(i);///如果有节点没有dfs访问到 
	}
	int ans=0;
	for (int i=1;i<=scctot;++i)///统计节点个数大于1的强连通分量的个数 
	{
		if (num[i]>1)ans++;
	}
	printf("%d",ans);
	return 0;
}

三、 点集和割集

对于图的连通性而言，不同节点或边的“重要性”是不同的，比如在通信网络中，有的节点或边出现中断，会对整个连通性的影响到头重要，而有的则不影响全局。另外，也存在一部分节点联合起来，从而对于整个图的连通性起关键作用。

一句话：点集和割集主要是为了研究，一些点的存在或者删除后对整个图的连通性影响。