机器学习——bp神经网络
目录
一、人工神经网络
1.简介
人工神经网络(Artificial Neural Network,即ANN ),是20世纪80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象, 建立某种简单模型,按不同的连接方式组成不同的网络。在工程与学术界也常直接简称为神经网络或类神经网络。神经网络是一种运算模型,由大量的节点(或称神经元)之间相互联接构成。
2.基本特征
人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。它是在现代神经科学研究成果的基础上提出的,试图通过模拟大脑神经网络处理、记忆信息的方式进行信息处理。人工神经网络具有四个基本特征:
- 非线性:非线性关系是自然界的普遍特性。大脑的智慧就是一种非线性现象。人工神经元处于激活或抑制二种不同的状态,这种行为在数学上表现为一种非线性关系。具有阈值的神经元构成的网络具有更好的性能,可以提高容错性和存储容量。
- 非局限性:一个神经网络通常由多个神经元广泛连接而成。一个系统的整体行为不仅取决于单个神经元的特征,而且可能主要由单元之间的相互作用、相互连接所决定。通过单元之间的大量连接模拟大脑的非局限性。联想记忆是非局限性的典型例子。
- 非常定性:人工神经网络具有自适应、自组织、自学习能力。神经网络不但处理的信息可以有各种变化,而且在处理信息的同时,非线性动力系统本身也在不断变化。经常采用迭代过程描写动力系统的演化过程。
- 非凸性:一个系统的演化方向,在一定条件下将取决于某个特定的状态函数。例如能量函数,它的极值相应于系统比较稳定的状态。非凸性是指这种函数有多个极值,故系统具有多个较稳定的平衡态,这将导致系统演化的多样性。
3.激活函数简介
激活函数的引入为的是增加整个网络的表达能力 (即非线性),否则,若干线性操作层的堆叠仍然只能起到线性映射的作用,无法形成复杂的函数。因为线性模型的表达能力通常不够,所以我们需要引入非线性因素来增加其表达能力。
激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。类似于人类大脑中基于神经元的模型,激活函数最终决定了要发射给下一个神经元的内容。
激活函数有多种,包括 Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、ELU、Maxout 等,常用的有Sigmoid,Tach,Relu这三种。
1.Sigmoid函数
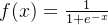
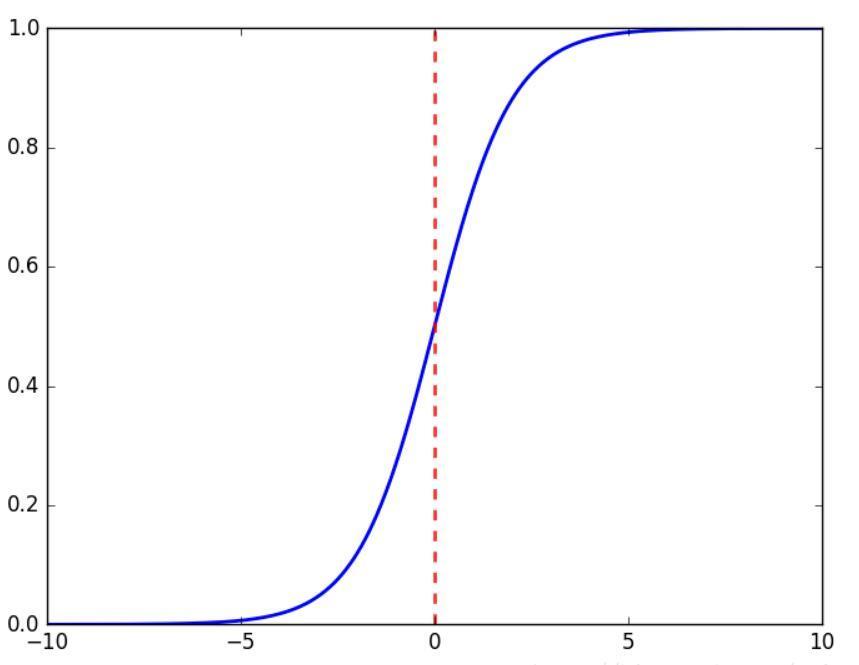
2.Tanh函数
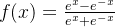
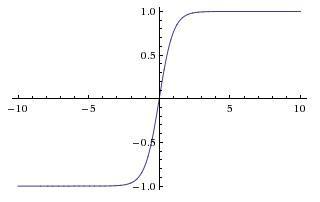
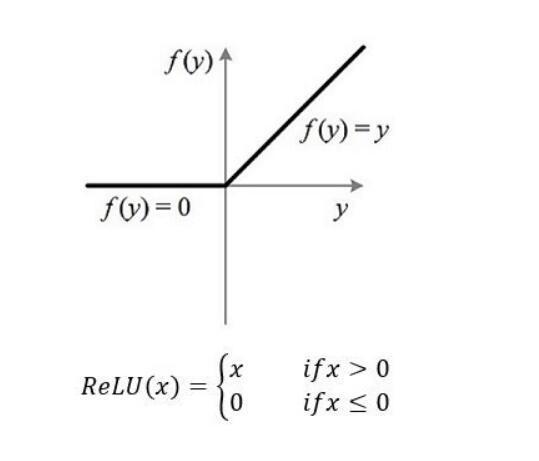
3.Relu函数
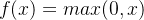
二、BP神经网络
Bp神经网络可以分为两个部分,bp和神经网络。bp(Back Propagation)的意思是反向传播。
它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
其主要的特点是:信号是正向传播的,而误差是反向传播的。
算法流程:
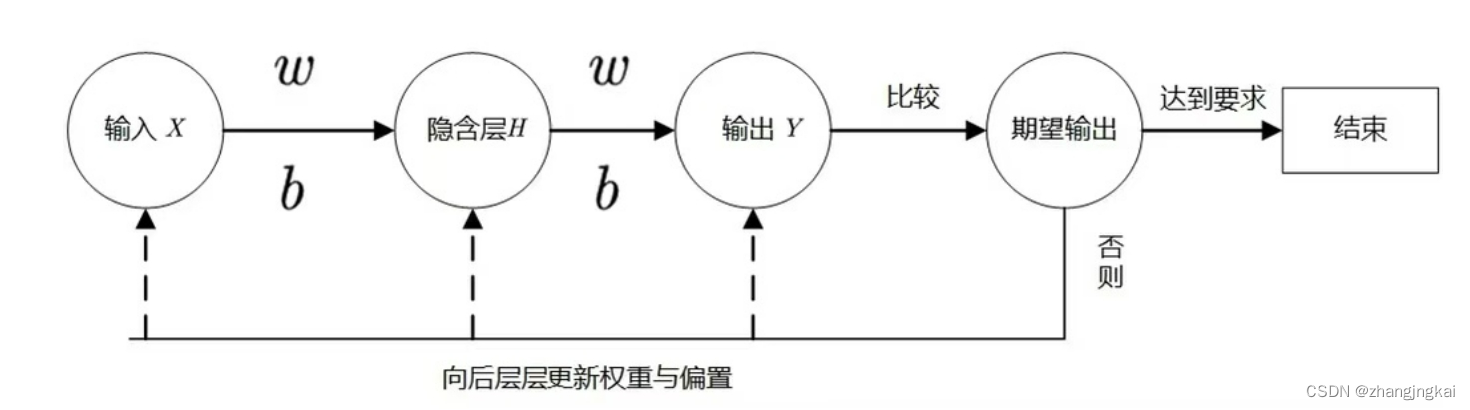
输入层:信息的输入端,是读入你输入的数据的
隐藏层:信息的处理端,可以设置这个隐藏层的层数(在这里一层隐藏层,p个神经元)
输出层:信息的输出端,也就是我们要的结果
BP神经网络的过程主要分为两个阶段,第一阶段是信号的正向传播,从输入层经过隐藏层,最后到达输出层;第二阶段是误差的反向传播,从输出层到隐藏层,最后到输入层,依次调节隐藏层到输出层的权重和偏置,输入层到隐含层的权重和偏置。
神经网络的结构:
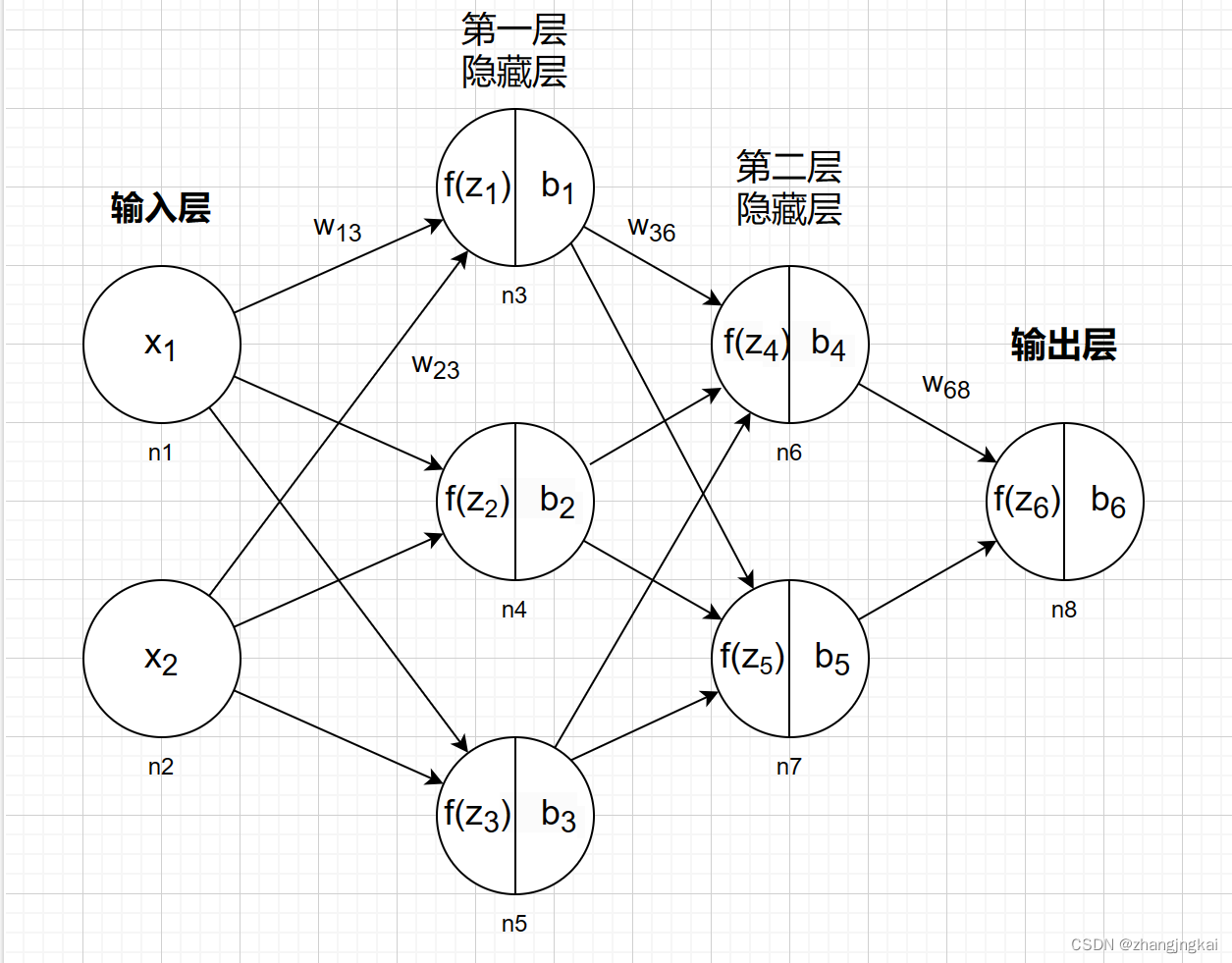
正向传播:
如图,有一个神经网络,为方便计算,将每个神经元依次命名为n1—n8;权重w也按神经元区分。
现在有两个隐藏层,输入层两个神经元,分别为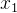 和
和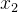 ,首先要计算第一层隐藏层的输入:
,首先要计算第一层隐藏层的输入:
n3的输入: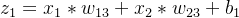
n4的输入: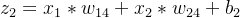
n5的输入:
然后就是这层隐藏层的输出,也就是经过激活函数,假设使用的激活函数都为sigmoid函数,第一层隐藏层的输出:
n3的输出: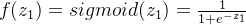
n4的输出: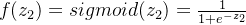
n5的输出: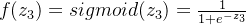
第二层隐藏层的输入:
n6的输入: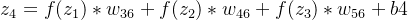
n7的输入: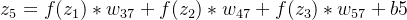
第二层隐藏层的输出:
n6的输出: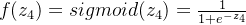
n7的输出: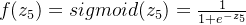
输出层的输入:
n8的输入: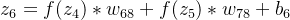
输出层的输出:
n8的输出: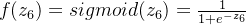
反向传播:
对于输出层的神经元,这个误差可以直接计算。对于隐藏层的神经元,误差是通过将其后一层的神经元的误差加权相加并应用激活函数的导数来计算的。
这个神经网络属于回归问题,所以我们使用均方误差作为损失函数。
损失函数: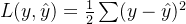
输出层误差等于损失函数关于输出层输入的梯度:
n8的误差: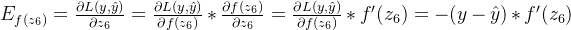
而输出层只有一个神经元,所以误差项:![E_{out}=[E_{f(z_6)}]](https://images2.imgbox.com/ab/55/q2PyYiWM_o.png)
第二层隐藏层神经元的误差:
n7的误差:![E_{f(z_5)}=\frac{\partial L(y,\hat{y})}{\partial z_5}=f'(z_5)*[w_{78}]^T*E_{out}](https://images2.imgbox.com/3e/66/qm90EJwJ_o.png)
n6的误差:![E_{f(z_4)}=\frac{\partial L(y,\hat{y})}{\partial z_4}=f'(z_4)*[w_{68}]^T*E_{out}](https://images2.imgbox.com/b2/53/fzFvoBd6_o.png)
这一层的误差项为: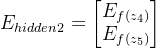
第一层隐藏层神经元的误差:
n5的误差: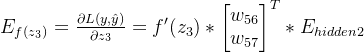
n4的误差: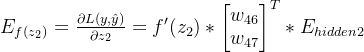
n3的误差: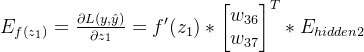
这一层的误差项为: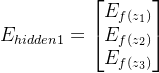
更新参数:
对于每个权重,其梯度等于后一层神经元的误差项乘以前一层神经元的输出。
权重的更新:
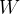 是相应权重组成的矩阵。
是相应权重组成的矩阵。
第二层隐藏层与输出层之间权重的更新: 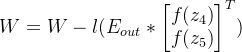
第一层隐藏层与第二层隐藏层之间权重的更新: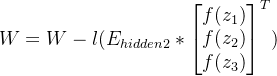
输入层与第一层隐藏层之间权重更新: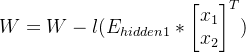
对于每个偏置,其梯度等于相应神经元的误差项。
第一层的隐藏层的偏置: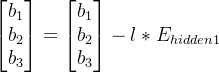
第二层的隐藏层的偏置: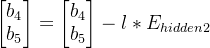
输出层的偏置: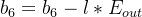
三、代码实现
下面是bp神经网络实现手写字识别
完整代码:
import numpy as np
# 定义sigmoid函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 定义one-hot编码函数,将类别标签转换为one-hot编码形式
def one_hot_encode(labels, num_classes):
one_hot = np.zeros((len(labels), num_classes))
one_hot[np.arange(len(labels)), labels] = 1
return one_hot
# 读取训练集和测试集
train_data = np.genfromtxt('mnist_train_100.csv', delimiter=',', skip_header=1)
test_data = np.genfromtxt('mnist_test_10.csv', delimiter=',', skip_header=1)
# 分离特征和标签并对特征进行归一化
X_train = train_data[:, 1:] / 255
Y_train = train_data[:, 0]
X_test = test_data[:, 1:] / 255
Y_test = test_data[:, 0]
# 对标签进行one-hot编码
Y_train_onehot = one_hot_encode(Y_train.astype(int), 10)
Y_test_onehot = one_hot_encode(Y_test.astype(int), 10)
# 定义bp神经网络
class NeuralNetwork:# 输入层节点 隐藏层节点 输出层节点 学习率
def __init__(self, input_nodes, hidden_nodes, output_nodes, learning_rate):
self.input_nodes = input_nodes
self.hidden_nodes = hidden_nodes
self.output_nodes = output_nodes
# 初始化权重(连接输入层和隐藏层的权重、连接隐藏层和输出层的权重)
self.weights_input_to_hidden = np.random.normal(0.0, self.input_nodes ** -0.5,(self.input_nodes, self.hidden_nodes))
self.weights_hidden_to_output = np.random.normal(0.0, self.hidden_nodes ** -0.5,(self.hidden_nodes, self.output_nodes))
# 初始化偏置项
self.bias_input_to_hidden = np.zeros(self.hidden_nodes)
self.bias_hidden_to_output = np.zeros(self.output_nodes)
self.lr = learning_rate
self.sigmoid = sigmoid
# 正向传播
def forward_pass(self, X):
hidden_inputs = np.dot(X, self.weights_input_to_hidden) + self.bias_input_to_hidden
hidden_outputs = self.sigmoid(hidden_inputs)
final_inputs = np.dot(hidden_outputs, self.weights_hidden_to_output) + self.bias_hidden_to_output
final_outputs = self.sigmoid(final_inputs)
return hidden_outputs, final_outputs
# 反向传播
def backward_pass(self, X, y, hidden_outputs, final_outputs):
output_errors = final_outputs - y
output_grad = output_errors * final_outputs * (1 - final_outputs) # 这里两步才是真正的误差项,这里乘的是sigmoid的导数
hidden_errors = np.dot(output_grad, self.weights_hidden_to_output.T)
hidden_grad = hidden_errors * hidden_outputs * (1 - hidden_outputs) # 也是和上面一样
return output_grad, hidden_grad
# 权重更新
def update_weights(self, X, output_grad, hidden_outputs, hidden_grad):
self.weights_hidden_to_output -= self.lr * np.dot(hidden_outputs.T, output_grad) / X.shape[0]
self.weights_input_to_hidden -= self.lr * np.dot(X.T, hidden_grad) / X.shape[0]
# 偏置更新
def update_bias(self, X, output_grad, hidden_grad):
self.bias_hidden_to_output -= self.lr * np.mean(output_grad, axis=0)
self.bias_input_to_hidden -= self.lr * np.mean(hidden_grad, axis=0)
# 训练模型
def train(self, X, y):
hidden_outputs, final_outputs = self.forward_pass(X)
output_grad, hidden_grad = self.backward_pass(X, y, hidden_outputs, final_outputs)
self.update_weights(X, output_grad, hidden_outputs, hidden_grad)
self.update_bias(X, output_grad, hidden_grad)
# 进行预测
def predict(self, X):
_, final_outputs = self.forward_pass(X)
return np.argmax(final_outputs, axis=1)
#设置参数
input_nodes = 784
hidden_nodes = 128
output_nodes = 10
learning_rate = 0.1
network = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
# 训练神经网络
for e in range(1000):
network.train(X_train, Y_train_onehot)
# 进行预测并计算准确率
predictions = network.predict(X_test)
accuracy = np.mean(predictions == Y_test)
print(f"Accuracy: {accuracy}")
我首先定义了sigmoid函数作为激活函数,还有将标签转换为one-hot形式,转换为 one-hot 编码可以更好地表达类别之间的差异。
定义神经网络时,严格按照步骤,为简化代码,只用了一层隐藏层。先进行正向传播,再反向传播误差,更新权重和偏置,然后进行训练、预测。最终输出预测的准确率。
运行结果:

由于权重初始化是随机的,在训练次数较少时准确率可能会变低。