秘密共享之算术共享、布尔共享
PS:一直以来都没有写东西的习惯,每次看完的东西想起来时总是手忙脚乱找不到依据,甚至很多看过很多遍的东西也一直遗忘。趁着2020年年末之际,尝试将一些有用的、会用的等知识进行整理,培养一下自觉性,也培养下思路逻辑啥啥啥的。
以下是对近些日子了解安全多方计算(Multi Party Computation,MPC)时碰到的相关概念的总结。
文章目录
1 秘密共享(Secret Sharing,SS)
秘密共享机制是在一组参与者中共享秘密的技术,它主要用于保护重要信息,防止信息被丢失、被破坏、被篡改[1]。(个人认为SS是MPC的基础)
以下转载自:知乎
秘密共享通过把秘密进行分割,并把秘密在n个参与者中分享,使得只有多于特定
t
t
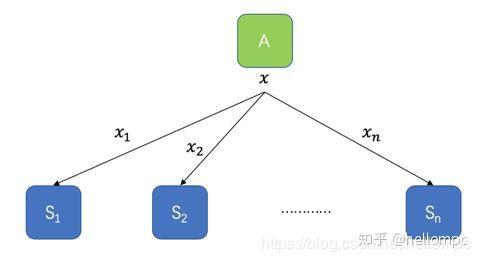
t个参与者合作才可以计算出或是恢复秘密,而少于t个参与者则不可以得到有关秘密。如下图所示,特征A的值x,分割成
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x1,x2,...,xn,分发给
S
1
,
S
2
,
.
.
.
,
S
n
S_1,S_2,...,S_n
S1,S2,...,Sn。
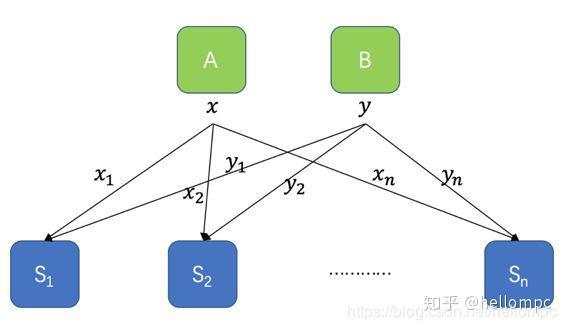
秘密共享体系还具有同态的特性。如下图所示:有特征A和B,他们的值被随机分成碎片
(
X
1
,
X
2
,
…
,
X
n
)
(X_1, X_2, …, X_n)
(X1,X2,…,Xn)和
(
Y
1
,
Y
2
,
…
,
Y
3
)
(Y_1, Y_2, …, Y_3)
(Y1,Y2,…,Y3),并分配到不同参与节点
(
S
1
,
S
2
,
…
,
S
n
)
(S_1,S_2, …, S_n)
(S1,S2,…,Sn)中,每个节点运算结果的加和,等同于原始A与B的加和。同样通过增加其他计算机制,也能满足乘积的效果,这就是秘密共享具备的“同态性”,各参与者可以在不交换任何数据的情况下直接对密码数据求和、乘积。
在秘密共享系统中,攻击者必须同时获得一定数量的秘密碎片才能获得密钥,通过这样能提高系统的安全性。另一方面,当某些秘密碎片丢失或被毁时,利用其它的秘密份额仍让能够获得秘密,这样可提高系统的可靠性。
2 算术共享(Arithmetic Sharing,AS)
算术共享是将一个数字按照简单数学运算形式(例如加法、乘法)进行分解、共享(个人理解)。形式化定义如下:(来源:Arithmetic Sharing(算术共享))
Sharing Values. For an k k k-bit Arithmetic sharing x x x of x, we have x 0 + x 1 = x ( m o d 2 k ) x_0 + x_1 = x (mod 2^k) x0+x1=x(mod2k) with x 0 , x 1 ∈ Z 2 k x_0,x_1 \in \Bbb{Z}_{2^k} x0,x1∈Z2k.
Sharing. P i P_i Pi chooses r ∈ R Z 2 k r \in_{R} \Bbb{Z}_{2^k} r∈RZ2k, set x i = x − r x_i=x-r xi=x−r and send r r r to P 1 − i P_{1-i} P1−i who sets x 1 − i = r x_{1-i}=r x1−i=r.
Reconstruction. P 1 − i P_{1-i} P1−i sends its share x 1 − i x_{1-i} x1−i to P i P_i Pi who computes x = x 0 + x 1 x=x_0+x_1 x=x0+x1.
3 布尔共享(Boolean Sharing,BS)
布尔共享,即是将算术共享中元素取值域 Z 2 k \Bbb{Z}_{2^k} Z2k变为 Z 2 \Bbb{Z}_{2} Z2,加法操作变为异或。(来源:Boolean Sharing(布尔共享))
Shared Values. A Boolean share s s s of a bit w w w is shared between the two parties.
Sharing. P i P_i Pi chooses r ∈ { 0 , 1 } r \in \{0, 1 \} r∈{0,1}, computes s 1 = w ⨂ r s_1=w \bigotimes r s1=w⨂r, and sends r r r to P 1 − i P_{1-i} P1−i who sets s 2 = r s_2=r s2=r.
Reconstruction. P 1 − i P_{1-i} P1−i sends its share s 2 s_2 s2 to P i P_i Pi who computes w = s 1 ⨂ x 2 w=s_1 \bigotimes x_2 w=s1⨂x2.
4 (补充)混淆电路(Garbled Circuits,GC)
混淆电路所了解不多,在此记录下在知乎上看到的比较浅显易懂的系列:混淆电路介绍(三)混淆电路原理
参考链接:
[1] https://zhuanlan.zhihu.com/p/114488222
[2] https://blog.csdn.net/qq_41369669/article/details/106150511
[3] https://blog.csdn.net/qq_41369669/article/details/106109232
渣硕小白一枚,欢迎大佬的批评、指正。希望每天进步一点点,争取早日脱离苦海。