【数据结构】（分治策略）中位数的查询和最接近点对问题

中位数查询：

寻找一组字符串中第k小的数，返回其值和下标。

不可以有重复值（在缩小规模的时候，会导致程序死循环）

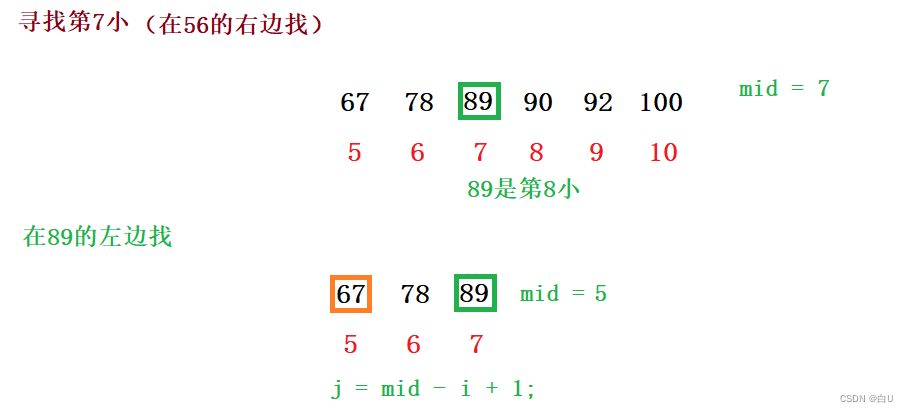
相对位置的转换体现了分治策略的思想。>

• 划分函数

int partition(int *nums,int left, int right)
{
	int i = left , j = right;
	int tmp = nums[i];
	while (i < j)
	{
		while (i<j && tmp < nums[j]) j--;
		if (i < j) nums[i] = nums[j];
		while (i<j && tmp >= nums[j]) i++;
		if (i < j) nums[i] = nums[j];
	}
	nums[i] = tmp;
	return i;
}

1.将待查询数组进行划分，得到num[left] 此时的下标 i（该值的下标将不会在变化）
2.i-left+1计算出i的相对位置j；
3.如果待查的k小于等于j，则从i的左边查，如果大于，从i的右边查。（说明i之前的下标都没有，则待查的k也减去相应j）
4.当只剩下一个元素，并且k等于1.返回当前值。

int selectK(int* nums, int left, int right, int k)
{
	if (left == right && k == 1) return nums[left];
	int i = partition(nums, left, right);
	int j = i - left + 1;//相对位置，在当前划分范围内
	if (k <= j) return selectK(nums, left, i, k);
	/* 优化，可以处理重复值
	if (k == j) return nums[i];
	if (k < j) return selectK(nums, left, i-1, k);
	*/
	else return selectK(nums, i+1, right, k-j);
}

int selectMin(int* nums, int n, int k)
{
	if (nums == nullptr
|| n < 1 || k<1 || k>n) return -1;
	return selectK(nums, 0, n - 1, k);
}

int main()
{
	int arr[] = { 56, 23, 78, 45, 90, 89, 12, 34, 67, 92, 100
	};
	int n = sizeof(arr) / sizeof(arr[0]);
	for (int i = 1; i < n - 1; i++)
	{
		int kmin = selectMin(arr, n, i);
		printf("%d:%d\n", i, kmin);
	}
	return 0;
}

最接近点对问题

找到一个中位数，将问题划分为两个规模，左边的所有数字小于该中位数，右边的所有数字均大于该中位数。用左边的最大值和右边的最小值做差。

1.当问题规模小于两个数，直接返回当前值（即为最大值）
2.通过计算，得到整个问题规模的中位数。
3.使用k+left-1得到pos。
4.利用查询中位数函数，将该数组中的数组划分为相同的两部分。
5.分别处理左半部分和右半部分。获得两部分的最小差值。
6.获得左边的最大值和右边的最小值。
7.比较 d1，d2, q-p的值。

不能直接是可得原因是，如0+10/2为5 ，取右边模块，（5+1）/2 = 3，需要再加上left减去1，才是处理右边真正得下标。

int SMin(int *nums,int left,int right)
{
	if ((right - left) < 1) return INT_MAX;
	int k = (right - left + 1) / 2;//找到最中间的值
	int pos = k + left - 1;//加上前面的偏移量left
	selectK(nums, left, right, k);
	//划分为规模相同的两部分。
	//计算出d1中的最小值，d2中的最小值差
	int d1 = SMin(nums, left, pos); //不能直接是可得原因是，如0+10/2为5 ，取右边模块，（5+1）/2 = 3，需要再加上left减去1，才是处理右边真正得下标。
	int d2 = SMin(nums, pos+1, right);
	int p = MaxS1(nums, left, pos);
	int q = MinS2(nums, pos+1, right);
	return Min3(d1, d2,q - p);
}


int SMinnum(int* nums,int n )
{
	if (nums == nullptr || n < 2) return INT_MAX;
	return SMin(nums, 0, n - 1);
}

• 获取右边的最小值，左边的最小值

int MaxS1(int* nums, int left, int right)
{
	return nums[right];//pos的值大于前面所有的值
}
int MinS2(int* nums, int left, int right)
{
	int tmp = nums[left];
	for (int i = left + 1; i <= right; ++i)
	{
		if (tmp > nums[i])
		{
			tmp = nums[i];
		}
	}
	return tmp;
}

• 获取三个数中的最小值。

int Min(int a, int b)
{
	return a < b ? a : b;
}
int Min3(int a, int b, int c)
{
	return Min(a, Min(b, c));
}