看书标记【R语言数据分析与挖掘实战】13
第十三章 基于数据挖掘技术的市政收入分析预测模型
13.1 背景与挖掘目标
正确处理地方财政与经济的相互关系具有十分重要的意义,建模目标:1)梳理影响地方财政收入的关键特征,分析、识别影响地方财政收入的关键特征的选择模型;2)结合目标1的因素分析,对广州2015年的财政总收入及各个类别收入进行预测。
13.2 分析方法与过程
常用多元线性回归模型,运用最小二乘估计对回归模型系数进行估计,以系数是否通过检验来验证其相关关系。这样得到的结果往往对数据的依赖程度很大,且OLS求得到的解往往是局部最优解,其相关检验可能会失去意义。针对预测变量过多,子集选择的计算过程操作不易问题,Lasso 成为了被广泛应用于参数估计和变量选择的方法之一。书中的案例选用了Adaptive-Lasso 方法探究地方财政收入与各因素之间的关系。lasso是由Tibshirani提出的将参数估计与变量选择同时进行的一种正则化方法,其参数估计定义如下:
β
^
(
l
a
s
s
o
)
=
arg
min
β
∣
∣
y
−
∑
j
=
1
p
x
j
β
j
∣
∣
2
+
λ
∑
j
=
1
p
∣
β
j
∣
\hat{\beta}(lasso)={\arg \min}_\beta||y-\sum_{j=1}^{p}x_j\beta_j||^2+\lambda \sum_{j=1}^{p}|\beta_j|
β^(lasso)=argminβ∣∣y−∑j=1pxjβj∣∣2+λ∑j=1p∣βj∣,lambda为非负正则参数,后一项为惩罚项。lasso本身有一些严苛的条件,之后Zou给不同的系数加上不同的权重,被称为Adaptive-Lasso方法:
β
∗
^
(
l
a
s
s
o
)
=
arg
min
β
∣
∣
y
−
∑
j
=
1
p
x
j
β
j
∣
∣
2
+
λ
n
∑
j
=
1
p
w
^
j
∣
β
j
∣
,
w
^
j
=
1
∣
β
^
j
∣
γ
\hat{\beta^*}(lasso)={\arg \min}_\beta||y-\sum_{j=1}^{p}x_j\beta_j||^2+\lambda_n \sum_{j=1}^{p}\hat{w}_j|\beta_j|,\hat{w}_j=\frac{1}{|\hat{\beta}_j|^\gamma}
β∗^(lasso)=argminβ∣∣y−∑j=1pxjβj∣∣2+λn∑j=1pw^j∣βj∣,w^j=∣β^j∣γ1,hat beta为OLS得到的系数。
之后建立灰色预测模型通过少量的、不完全的信息,建立数学模型并做出预测。
1、灰色预测与神经网络的组合模型
在Adaptive-Lasso变量选择的基础上,灰色预测对小数量数据预测的优良性能,而神经网络具有较强的适用性和容错能力,可以对历史数据建立训练模型,所以书中把灰色预测的数据结果代入训练好的模型中,就得到了充分考虑历史信息的预测结果。
1) 从某市统计局网站以及各统计年鉴搜集到该市财政收入以及各类别收入相关数据;
2) 利用1)形成的已完成数据预处理的建模数据,建立Adaptive-Lasso变量选择模型;
3) 在2)的基础上建立单变量的灰色预测模型以及人工神经网络预测模型;
4) 利用3)的预测值代入构建好的人工神经网络模型中,从而得到2014/2015年某市财政收入以及各类别收入的预测值。
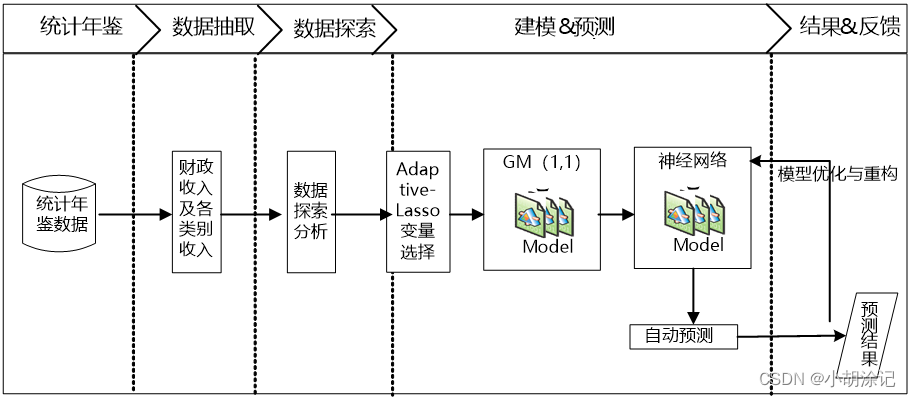
2、数据探索分析
Y,财政收入;以及X1~X13的自变量。
先对变量进行描述分析,均为连续型变量;相关性分析,初步判断全部变量间是否具有线性相关性,书中用到的是Pearson相关系数。
##描述性统计
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter13/示例程序")
# 读入数据
Data <- read.csv("./data/data1.csv", header = TRUE)[, 2:15]
# 数据概括性度量
Min <- sapply(Data, min) # 最小值
Max <- sapply(Data, max) # 最大值
Mean <- sapply(Data, mean) # 均值
SD <- sapply(Data, sd) # 方差
cbind(Min, Max, Mean, SD)
## 相关性分析
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter13/示例程序")
# 读入数据
Data <- read.csv("./data/data1.csv", header = TRUE)[, 2:15]
# pearson相关系数,保留两位小数
round(cor(Data, method = c("pearson")), 2)
3、模型构建
书中用的是LARS算法解决的Adaptive-Lasso估计,对于每个gamma,LARS算法会找到一个最优的lambda,此处lambda=1,运行得到的各变量的的估计系数。
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter13/示例程序")
# 读入数据
Data <- read.csv("./data/data1.csv", header = TRUE)
# 加载adapt-lasso源代码
source("./code/lasso.adapt.bic2.txt")
out1 <- lasso.adapt.bic2(x = Data[, 1:13], y = Data$y)
# adapt-lasso输出结果名称
names(out1)
# 变量选择输出结果序号
out1$x.ind
# 保留五位小数
round(out1$coeff, 5)
# 保存adapt-lasso模型
save(out1, file = "./tmp/out1.RData")
系数接近0的变量表示在建模的过程中适合剔除,结合案例可以认为这几个变量对于其他的变量存在明显的共线关系。这一过程也说明Adaptive-Lasso方法在建模时,能够剔除存在共线性关系的变量,同时体现了Adaptive-Lasso方法对多指标进行建模的优势。
之后对y及筛选出来的变量(X1,X2,X3,X4,X5,X7)进行灰色预测和神经网络的组合模型的构建。先用灰色预测模型对6个自变量进行预测,得到2014年的预测值,然后代入神经网络构建的训练模型,得到y的预测值。相当于神经网络在此处预测X 就不是很合适?
##灰色预测模型
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter13/示例程序")
# 读入数据
Data <- read.csv("./data/data1.csv", header = TRUE)
attach(Data)
# 加载GM(1, 1)源文件
source("./code/gm11.txt")
gm11(x1 / 10000, length(x1 / 10000) + 2)
gm11(x2, length(x2) + 2)
gm11(x3, length(x3) + 2)
gm11(x4, length(x4) + 2)
gm11(x5, length(x5) + 2)
gm11(x7, length(x7) + 2)
##神经网络预测模型
# 设置工作空间
setwd("D:/test")
library(nnet)
# 读入数据
Data <- read.csv("./data/revenue.csv", header = FALSE)
asData <- scale(Data)
colnames(asData) <- c("x1", "x2", "x3", "x4", "x5", "x7", "y") # 每列列名
nn <- nnet(y ~ ., asData[1:22, ], size = 6, decay = 0.00000001,
maxit = 10000, linout = T, trace = T)
predict <- predict(nn,asData[, 1:6])
predict <- predict * sd(Data[1:22, 7]) + mean(Data[1:22, 7])
a <- 1994:2015
# 画出序列预测值、真实值图像
plot(predict, col = 'red', type = 'b', pch = 16, xlab = '年份',
ylab = '地方财政收入 / 万元', xaxt = "n")
points(Data[1:22, 7], col = 'blue', type = 'b', pch = 4)
legend('topleft', c('地方财政收入预测值', '地方财政收入真实值'),
pch = c(16, 4), col = c('red', 'blue'))
axis(1, at = 1:22, labels = a)
同样的步骤对增值税y1、营业税y2、企业所得税y3、个人所得税y4和政府性基金收入进行建模预测,步骤都是一样的,区别仅在与Adaptive-Lasso得到的自变量每次会因为y的不同而筛选得到不同变量。
(以前看过很多关于LASSO 的算法,觉得很不错,但是在实际应用中还是会感到不好通过模型对实际案例进行解释)