数据结构与算法——队列
概述
计算机科学中,queue 是以顺序的方式维护的一组数据集合,在一端添加数据,从另一端移除数据。添加的一端称为尾,移除的一端称为头。
功能
- 插入offer(value : E) : boolean
- 取值并移除poll() : E
- 取值peek() : E
- 判断是否为空isEmpty() : boolean
- 判断队列是否满isfull() : boolean
接口代码
public interface Queue<E> {
/**
* 向队列尾插入值
* @param value 待插入值
* @return 插入成功返回 true, 插入失败返回 false
*/
boolean offer(E value);
/**
* 从对列头获取值, 并移除
* @return 如果队列非空返回对头值, 否则返回 null
*/
E poll();
/**
* 从对列头获取值, 不移除
* @return 如果队列非空返回对头值, 否则返回 null
*/
E peek();
/**
* 检查队列是否为空
* @return 空返回 true, 否则返回 false
*/
boolean isEmpty();
/**
* 检查队列是否已满
* @return 满返回 true, 否则返回 false
*/
boolean isFull();
}链表实现
利用单向环形带哨兵链表实现
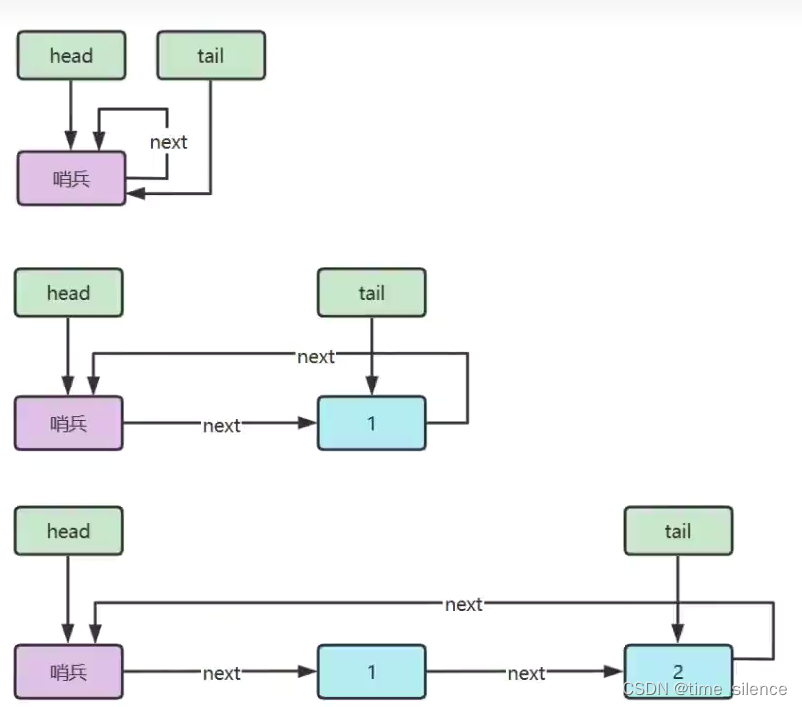
代码
import java.util.Iterator;
import java.util.StringJoiner;
/**
* 基于单向环形链表实现
* @param <E> 队列中元素类型
*/
public class LinkedListQueue<E>
implements Queue<E>, Iterable<E> {
private static class Node<E> {
E value;
Node<E> next;
public Node(E value, Node<E> next) {
this.value = value;
this.next = next;
}
}
private final Node<E> head = new Node<>(null, null);
private Node<E> tail = head;
int size = 0;
private int capacity = Integer.MAX_VALUE;
{
tail.next = head;
}
public LinkedListQueue() {
}
public LinkedListQueue(int capacity) {
this.capacity = capacity;
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
Node<E> added = new Node<>(value, head);
tail.next = added;
tail = added;
size++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
Node<E> first = head.next;
head.next = first.next;
if (first == tail) {
tail = head;
}
size--;
return first.value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return head.next.value;
}
@Override
public boolean isEmpty() {
return head == tail;
}
@Override
public boolean isFull() {
return size == capacity;
}
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
Node<E> p = head.next;
@Override
public boolean hasNext() {
return p != head;
}
@Override
public E next() {
E value = p.value;
p = p.next;
return value;
}
};
}
@Override
public String toString() {
StringJoiner sj = new StringJoiner(",");
for (E e : this) {
sj.add(e.toString());
}
return sj.toString();
}
}
数组实现
利用移位与相与操作,解决超长队列问题。
代码
import java.util.Iterator;
/**
* 仅用 head, tail 判断空满, head, tail 需要换算成索引值
*
* @param <E> 队列中元素类型
*/
public class ArrayQueue3<E> implements Queue<E>, Iterable<E> {
/*
求模运算:
- 如果除数是 2 的 n 次方
- 那么被除数的后 n 位即为余数 (模)
- 求被除数的后 n 位方法: 与 2^n-1 按位与
*/
private final E[] array;
private int head = 0;
private int tail = 0;
@SuppressWarnings("all")
public ArrayQueue3(int c) {
// 1. 抛异常
/*if ((capacity & capacity - 1) != 0) {
throw new IllegalArgumentException("capacity 必须是2的幂");
}*/
// 2. 改成 2^n 13 -> 16 22 -> 32
int n = (int) (Math.log10(c-1) / Math.log10(2)) + 1;
array = (E[]) new Object[1 << n];
/*
2^4 = 16
2^4.? = 30
2^5 = 32
(int)log2(30) + 1
2
log2(x) = log10(x) / log10(2)
1
10 2^1
100 2^2
1000 2^3
*/
}
/*
head = 0
tail = 3 % 3 = 0
capacity=3
0 1 2
d b c
*/
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
array[tail & (array.length - 1)] = value;
tail++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
int idx = head & (array.length - 1);
E value = array[idx];
array[idx] = null; // help GC
head++;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return array[head & (array.length - 1)];
}
@Override
public boolean isEmpty() {
return head == tail;
}
@Override
public boolean isFull() {
return tail - head == array.length;
}
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E value = array[p & (array.length - 1)];
p++;
return value;
}
};
}
}
补充
力扣题目
来源
路漫漫其修远兮,吾将上下而求索。