【论文阅读】（2023）Lower and Upper Bounding Procedures for the Bin Packing Problem with Concave Loading...

文章目录

一、Abstract 摘要
二、Introduction 介绍
三、Literature review 文献综述
四、Mathematical programming formulations 数学规划公式
- 4.1 An exponential set partitioning formulation of the BPPC BPPC的指数集划分公式
- 4.2 A polynomial formulation for the piecewise-linear case 分段线性情况下的多项式公式
五、Lower Bounds 下界
六、Heuristics 启发式方法
七、Computational results 计算结果
八、Conclusion 结论

论文来源：（2023）Lower and Upper Bounding Procedures for the Bin Packing Problem with Concave Loading Cost
作者：Mohamed Haouari 等人

一、Abstract 摘要

我们解决一维仓包装问题凹装载成本(BPPC)，这通常出现在小于卡车装载的运输服务。
我们的贡献是双重的。首先，我们提出了这个问题的两个下界。第一个问题是问题的连续松弛的最优解，并提出了一个封闭形式。第二个下界是基于大规模集划分公式的问题。
为了避免目标函数系数的非线性所带来的挑战，我们考虑了凹负荷代价的内部逼近，并推导了一个通过列生成来求解的简化公式。
此外，我们提出了两种基于子集和的启发式方法。第一种是建设性的启发式，而第二种是局部搜索启发式，通过选择箱对并解决相应的子集和问题，迭代地尝试改进当前的解决方案。
我们证明了任何BPPC启发式和任何凹加载代价函数的最差情况性能都以2为界。
我们展示了在大型基准实例集上进行的广泛计算研究的结果。
本研究提供的经验证据表明，基于列生成的下界和局部搜索启发式始终表现出出色的性能。

二、Introduction 介绍

一维箱子装箱问题(BPP)是一个基本的np困难问题，它要求将一组不同重量的物品装入最少数量的具有相同容量的箱子中。

这个模型具有欺骗性的简单性，它体现了组合优化问题的纯粹复杂性和巨大的通用性，在过去五十年的运筹学文献中引起了相当大的兴趣(Martello和Toth (1990);科尔特和维根(2006))。作为这项研究工作的一部分，研究了这个基本问题的大量变体。研究最多的是，可以说，二维仓包装问题(Lodi等人(2002))和可变大小的仓包装问题(Haouari和Serairi(2011))。

在本文中，我们研究了标准BPP的一个不同的推广，其中成本是由每个仓的总负载引起的。该成本是料仓装载的凹函数。问题在于将一组重量不等的物品放入无限数量的箱子中，以使装箱费用的总和最小化。

我们把这个问题称为凹仓装载成本的仓装问题(简称BPPC)。BPPC的正式定义如下。
我们给定：

满足 $f (0) = 0$ 的非递减凹函数 $f (.)$
无限数量的容量为 $Q$ 的相同箱子
n个项目的集合J，其中每个项目j∈J有一个非负整数权 $w_j≤Q$

BPPC要求将 $J$ 个物料装入 $m$ 个箱中，同时保证每个箱 i 的装载 $W_i$ 满足 $W_i≤Q (i = 1，…， m)$ ， $\sum_{i=1}^m f\left(W_i\right)$ 为最小值。

BPPC适用于少于卡车(LTL)运输服务，物流公司通常提供增量折扣，以鼓励托运人增加出货量。为了说明这种类型的应用程序，我们考虑一个位于法国巴黎的假设公司的情况，该公司将一些托盘的路由分包给一家卡车运输公司到荷兰阿姆斯特丹。

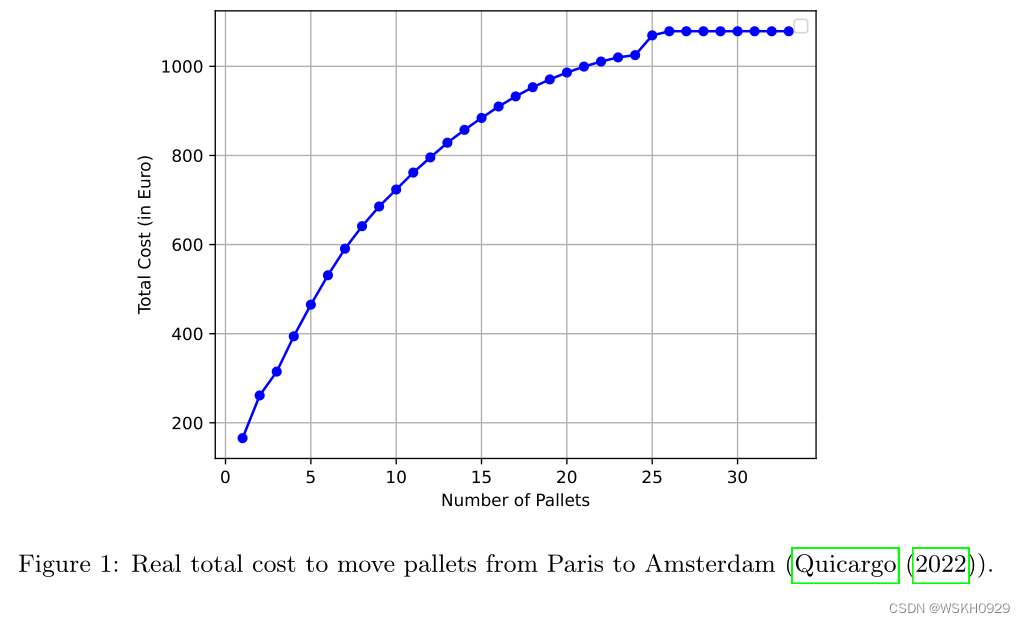
目前在欧洲，卡车公司根据托盘数量进行这种路由的实际成本如图1所示。所显示的曲线来自Quicargo(2022)网站提供的真实数据。在这个例子中，我们看到卡车容量为33个托盘，除了24个托盘负载的异常外，成本函数是凹的。这种凹形(或近似凹形)轮廓，在实践中转化为每增加一个托盘的运输提供一个递减的单价，在世界上通常应用于少于卡车载重的公司。显然，一个公司想要与少于卡车装载量的公司签订合同，将托盘从一个原产地城市运送到位于同一目的地城市的一组客户，将寻求解决BPPC，以确定哪些订单应该分配给哪辆卡车，以最小化其运输成本。

在这里插入图片描述
在本文中，我们提出并分析了BPPC的两个下界和两个启发式的经验性能。第一个下界是通过求解问题的连续松弛得到的，第二个下界是通过内近似和列生成得到的。

这两个边界的共同特征是，它们都是直接从具有凹分段线性代价函数的BPPC的一个重要特例的分析中推导出来的。另一方面，这两种启发式方法都要求子集和问题序列的最优解。

三、Literature review 文献综述

尽管有实际意义，但关于BPPC的文献很少。事实上，使用关键字“bin”和“packing”搜索Web of Science Core Collection，并将搜索范围限制在“运筹与管理科学”类别，就会发现813篇发表的参考文献。相反，在查询中添加关键字“凹”将搜索输出减少到9个文档。对后一篇参考文献的彻底检查表明，迄今为止，只有两篇论文涉及BPPC。

在第一篇论文中，Li和Chen(2006)引入了BPPC，并利用学习效应促使其应用于货物运输和生产调度。他们观察到该问题在强意义上是NP-hard问题，并分析了四种著名的BPP启发式算法的最差情况性能:第一拟合(FF)、最佳拟合(BF)、第一拟合递减(FFD)和最佳拟合递减(BFD)。他们发现FF和BF的最差性能比为2，而FFD和BFD的最差性能比为1.5。在第二篇论文中，Leung和Li(2008)提出了BPPC的多项式时间逼近算法。

他们表明，对于任何 $\epsilon$ > 0 的最坏情况，都存在一个多项式时间算法，其最坏情况性能比为1 + $\epsilon$ 。此外，应该指出的是，一个相关的，尽管不同，具有凹成本函数的箱子包装问题已经在文献中被解决了。

对于这个问题，容器的成本是容器中所装物品数量的凹函数，目标是找到总成本最小的包装。Anily et al.(1994)和Epstein and Levin(2012)分别研究了这个问题，称为具有一般成本结构的箱子包装问题。

前者研究了一些著名的装箱启发式算法的最坏情况性能，后者描述了该问题的渐近多项式-时间逼近格式。显然，与BPPC相关的出版物的缺乏不应该掩盖一个事实，即对BPP及其变体的研究仍然非常活跃。

以下是一些值得注意的近期发展的简要概述。Delorme和Iori(2019)提出了一种改进的伪多项式弧流公式，称为反射，用于标准BPP。作者发现这个公式始终优于de Carvalho的经典弧流公式(1999)，与Belov和Scheithauer(2006)的最先进的分支-切割-价格算法以及Brand ao和Pedroso(2016)的VPSolver相比非常优越。另一方面，Wei等人(2019)针对同一问题提出了一种新的精确分支-价格-削减(BPC)算法。他们的BPC具有许多算法权宜货，其中一个用于定价问题的高效标签设置算法，使得优化解决多达1,003个项目的大规模实例变得可行。

对于二维bin packing问题，Serairi and Haouari(2018)对下界进行了全面的理论分析，C ot´e et al.(2021)提出了一种增强的精确Benders分解算法。后一种方法解决了许多开放基准测试实例。最近，Iori等人(2021)提出了一项关于各种二维包装问题的调查。在他们的研究中，作者描述了许多包装问题的变化，其中物品和箱子是矩形的，主要集中在精确的方法，配方和松弛。标准箱包装问题的一个有趣的推广是矢量包装问题，其中为每个项目和每个箱定义了两个属性，因此加载每个箱必须满足两个容量约束。在这种情况下，Heßler等人(2018)提出了一种分支和价格算法来精确解决矢量包装问题。此外，Wei等人(2020)针对二维矢量打包问题提出了一种精确的分支和价格算法，其目标是最小化箱子的数量。

另一方面，Wang等人(2022)解决了后一个问题的新变体，该问题考虑了体积重量的更现实的代价函数。最近，Dell’amico等人(2020)提出了所谓的临时仓包装问题(TBPP)。在此变体中，为每个项目额外定义了时间范围和特定的时间窗口。如果一个项目被加载到一个bin中，那么它将在整个时间窗口的持续时间内填充该bin。这个问题要求将所有物品装入最少数量的箱子中，以便在任何时候都不会超过箱子的容量。作者提出了一个多项式和一个指数大小的公式，并开发了一个精确的分支和价格算法。同样，aydain等人(2020)在将虚拟机分配给云计算服务中的物理服务器的上下文中描述了TBPP的一个有趣应用。

为了开发优化模型以确保服务器的节能运行，Martinovic等人(2021)和Martinovic等人(2022)最近也研究了类似的变体。

最后，我们用Braune(2019)的论文来总结这篇简明的文献综述，他研究了一维仓位包装的一种变体，该变体与本文研究的模型具有共同的特征，即目标函数与仓位使用直接相关。事实上，作者研究了一个箱子包装问题的下界方案，其中可变成本与分配到箱子中的物品的累积重量相关，并且成本系数随箱子指数线性增加。

四、Mathematical programming formulations 数学规划公式

在本节中，我们将介绍两个数学规划公式，稍后将使用它们来推导BPPC的下界。

4.1 An exponential set partitioning formulation of the BPPC BPPC的指数集划分公式

我们用P表示可行包装模式的集合。每个模式 p∈P 可以用一个对应的二元关联向量 $A_p=\left(a_{j p}\right)_{j=1, \ldots, n}$ 表示。模式 $p$ 的成本为：
在这里插入图片描述
我们为每个模式 $p \in P$ 定义一个二进制决策变量 $\xi_p$ ，如果一个 bin 是根据模式 $p$ 填充的，则该变量的值为1，否则为0。

BPPC可以表述如下：

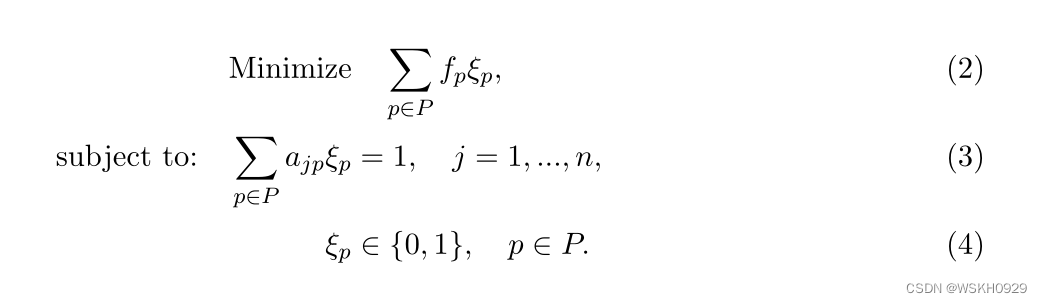
在这里插入图片描述

目标函数(2)要求总代价最小。
约束(3)强制每个项目被分配到一列。
约束(4)强制决策变量是二进制的。

4.2 A polynomial formulation for the piecewise-linear case 分段线性情况下的多项式公式

在本节中，我们提出了BPPC的一个特殊情况下的公式，即料仓的装载成本是一个非递减分段线性函数。为此，我们假设单位仓的利用成本是一个离散的步进递减函数。

因此，我们得到一组 $K + 1$ 个断点 $b_0，…， b_K$ ，令 $b_0 = 0$ , $b_K = Q$ ，且 $b_{k−1} < b_k , k = 1，…， K$ ，加上一组 K 个斜率 $c_1，…， c_K$ ，令 $c_1 >…> c_K$ 。如果分配到一个bin中的项目的累积权重为 $z∈(b_{k−1},b_k]$ ，则对应的 bin 利用率成本为：
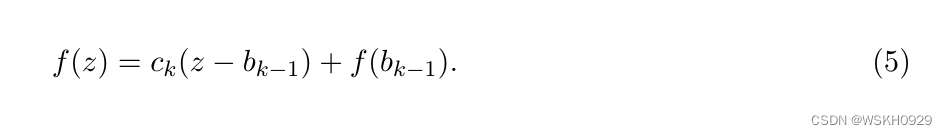
在这里插入图片描述
因此，我们得到：

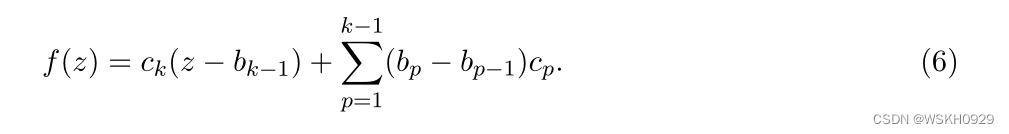
在这里插入图片描述

我们通过设置来观察

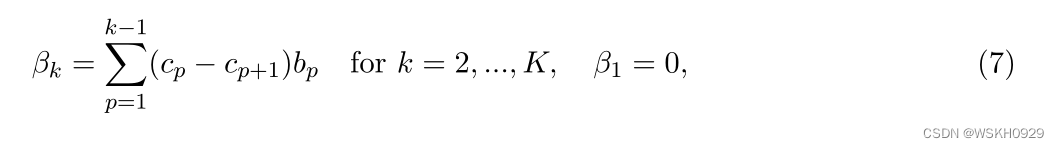
在这里插入图片描述
我们重新陈述箱子的使用成本如下：

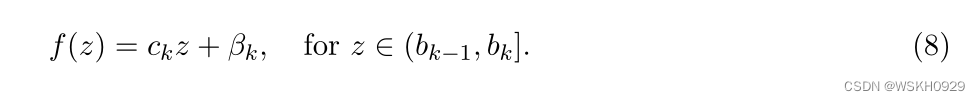
在这里插入图片描述
我们定义以下决策变量：

符号	含义
$x_{ij}$	二进制变量，如果项 j 赋值给 bin i，则值为1，否则为0。 $i, j = 1, \dots, n$
$y_{ik}$	二进制变量，如果容器 i 的总负载属于 $b_{k−1},b_k]$ ，则值为1，否则为0。 $i = 1, \dots, n; k = 1, \dots, K$
$z_{ik}$	连续变量，如果 $y_{ik} = 1$ ，它等于容器 i 的总负载，否则它就为0。 $i = 1, \dots, n; k = 1, \dots, K$

使用这些符号，一个有效的分段线性函数的BPPC混合整数规划公式如下。

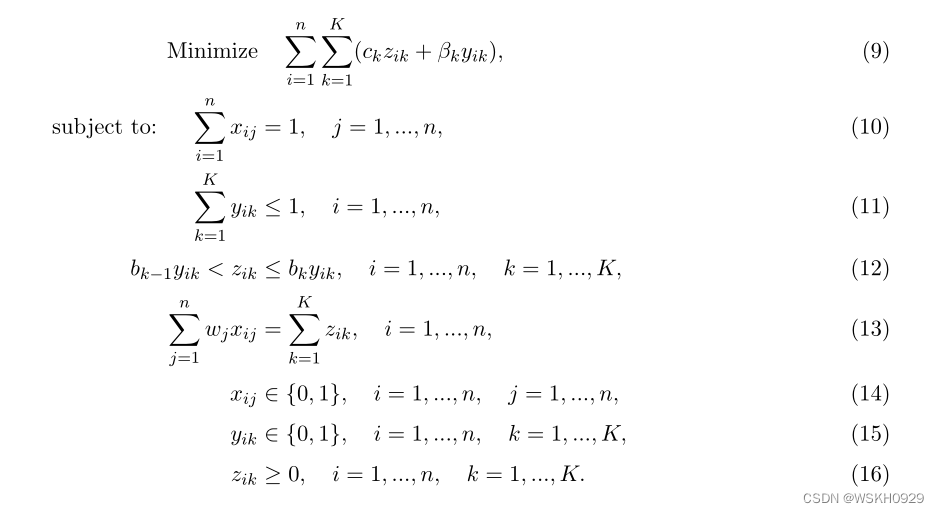
在这里插入图片描述

目标函数(9)等于最小化总成本。

约束(10)要求每个项目被分配到一个bin中。

约束(11)指定一个 bin 的总负载最多属于一个区间 $(bk - 1, bk], (k = 1, \dots, K)$

约束(12)强制规定，如果 $y_{ik} = 1$ ，则容器 i 的负载应严格大于 $b_{k−1}$ 且小于或等于 $b_k$ 。

在实践中，严格不等式被以下不等式取代：

在这里插入图片描述
其中 $κ$ 代表机器精度。

约束(13)强制，如果 $z_{ik} > 0$ ，则bin的总负载等于分配的项目的和。

最后，(14)-(16)指定决策变量域。

五、Lower Bounds 下界

5.1 The continuous lower bound 连续下界

首先，让我们考虑分段线性凹函数的特殊情况。在这种情况下，通过求解模型(9)-(16)的连续松弛，可以得到一个简单的下界。

这个松弛的最佳值如下。

引理1：模型(9)-(16)连续下界的最优值为：

证明：首先，我们观察到，由于 $β_k$ 对每一个 $k$ 严格为正，那么由式(12)，一个最优连续解满足：

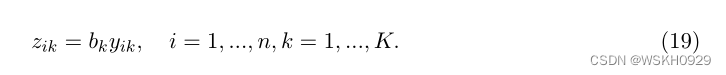
在这里插入图片描述

现在，我们证明了对于所有 $\neq K$ ，总有一个满足 $y_{ik} = 0$ 的最优连续解。

的确，假设存在一个代价为 $Z (S)$ 的连续最优解 $S (x, y, z)$ ，使得对于某些 i 和某些 $\neq K$ , $y_{ik} > 0$ 。我们推导出一个新的解 $\bar{S}(\bar{x}, \bar{y}, \bar{z})$ ，定义如下：

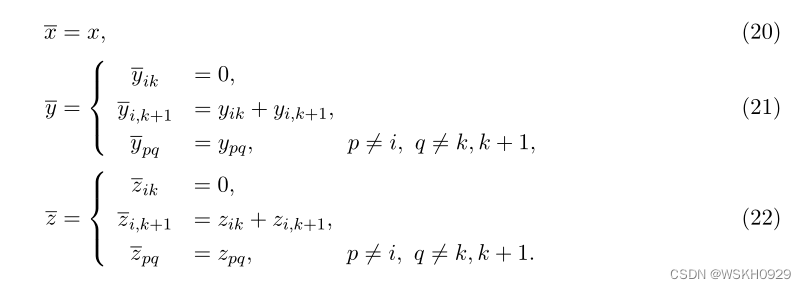
在这里插入图片描述

显然，为了证明 $\bar{S}$ 是可行的，我们只需要证明 $z_{i,k+1}$ 满足约束(12)

事实上，我们有：

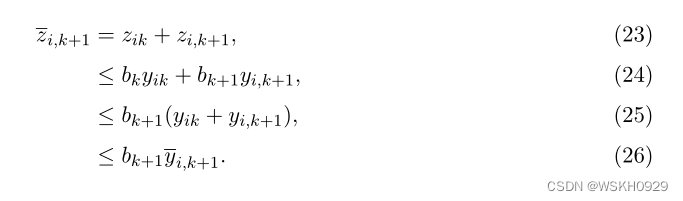
在这里插入图片描述

另一方面， $b_k)$ 是断点序列，满足：

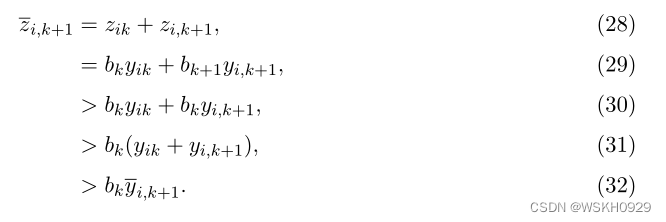
在这里插入图片描述

因此，我们有：

在这里插入图片描述

由式(26)和式(32)可知， $\bar{z}_{i,k+1}$ 满足约束(12)，因此 $\bar{S}$ 是可行的。

此外，我们还表明，成本差 $\Delta=Z(\bar{S})-Z(S)$ 为零。事实上，我们有：

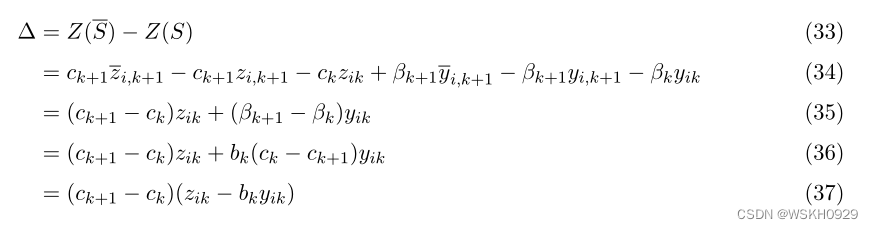
在这里插入图片描述

因此，使用(19)，我们得到：

在这里插入图片描述

因此，通过重复这个过程，我们推断，对于所有的箱子和所有的 $\neq K$ ，总是有可能推导出满足 $y_{ik} = 0$ 的最优解：

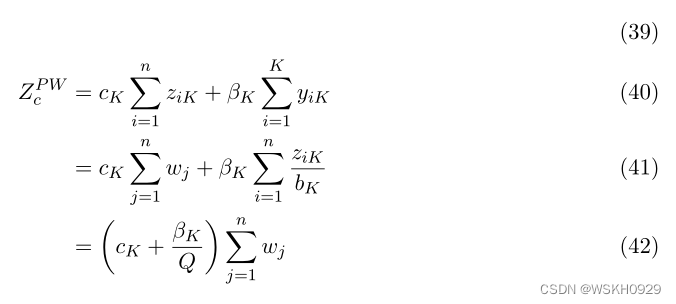
在这里插入图片描述

现在，我们考虑定义在 $[0, Q]$ 上的连续可微非递减凹函数 $f (.)$ 的一般情况。

引理2：连续可微非递减凹函数 $f (.)$ 的有效下界为:

证明： $f (.)$ 的分段外近似，以下表示为 $\tilde{f}_K(.)$ ，使用 $K + 1$ 个断点 $b_0，…，b_K$ ，使 $b_k=\frac{k Q}{K},k=0,...,K$

据此，设：

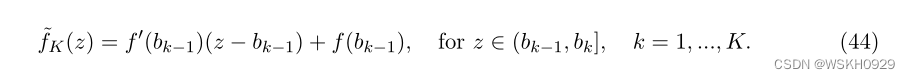
在这里插入图片描述

因此，在每个区间 $b_{k−1},b_k]$ 上， $\tilde{f}_K(.)$ 是 $f (.)$ 的一阶泰勒近似。利用引理1，令 $c_k = f ' (b_{k−1}),k=1,…,K$ 。我们推导出了问题的连续界，该问题是通过设置 $\tilde{f}_K(.)$ 作为 $f (.)$ 的近似值得到的。我们得到：

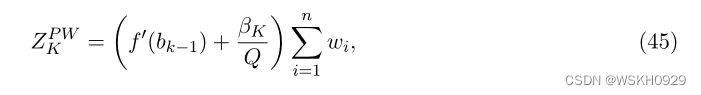
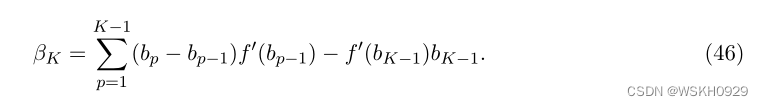
在这里插入图片描述

因此， $β_K$ 可以重述为以下形式

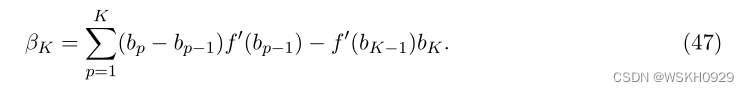
在这里插入图片描述

显然，我们有：

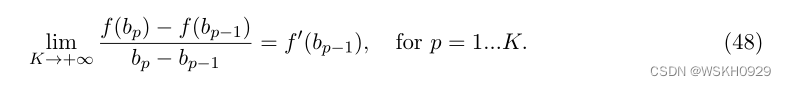
在这里插入图片描述

因此，利用 $b_K = Q$ 的事实，我们推导出：

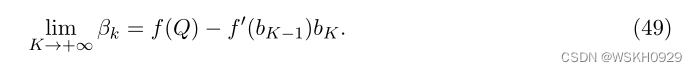
在这里插入图片描述

因此

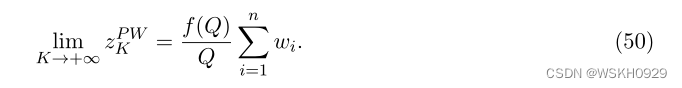
在这里插入图片描述

利用 $\tilde{f}_K(.)$ 无症状地收敛于 $f (.)$ 这一事实，我们得出结论：

在这里插入图片描述

5.2 Column generation 列生成

作为第二个下界，我们提出解决集划分模型(2)-(4)的连续松弛问题。每列的系数代价 $A_j$ 是 $A^t_jw$ 的非线性凹函数。

为了简单起见，我们考虑了该模型的一种变体，即用内近似分段线性函数代替真正的非线性凹荷载函数。

这个近似值，以后记为 $f (.)$ ，是用 $K + 1$ 个断点 $b0,…,b_K$ 使 $b_k=\frac{k Q}{K}$ , for $\ldots, K$ 。因此，我们设：

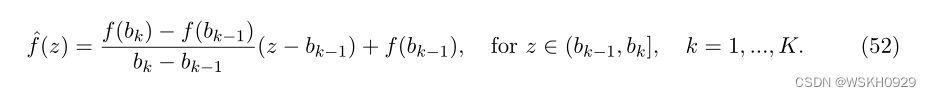
在这里插入图片描述

参数 $K$ 是经验设置的。由于 $f (.)$ 是凹的，那么对于 $z \in [0, Q]$ ，就可以得出： $\hat{f}(z)≤f(z)$ 。

因此，我们为每个包装 $p \in P$ 定义其成本的一个低估值：

在这里插入图片描述

因此，将目标函数中的实际成本系数替换为各自的低估值得到的集划分模型是对模型(9)-(16)的松弛。

因此，这个公式的线性规划松弛产生了一个有效的下界。

然而，由于它包含指数数量的变量，我们建议使用列生成来解决它。

5.3 The pricing algorithm 定价算法

找到具有最小降低成本的列相当于解决以下定价问题：

在这里插入图片描述

其中 $u_j$ 表示与模型(2)-(4)的 $j^{th}$ 约束相关联的对偶变量。定价问题可以表述为如下的 MIP 。

决策变量：

符号	含义
$x_j$	二进制变量，如果项 j 被赋值为1，则赋值为0，否则 $j = 1 ， \dots n$
$y_k$	二进制变量，如果容器的总负载为 $b_{k−1},b_k]$ ，则为1，否则为0 ， $k = 1, \dots, K$
$z_k$	连续变量，如果 $y_k = 1$ ，它等于容器的总负载，否则为0

使用这些定义，定价问题可以表述为：

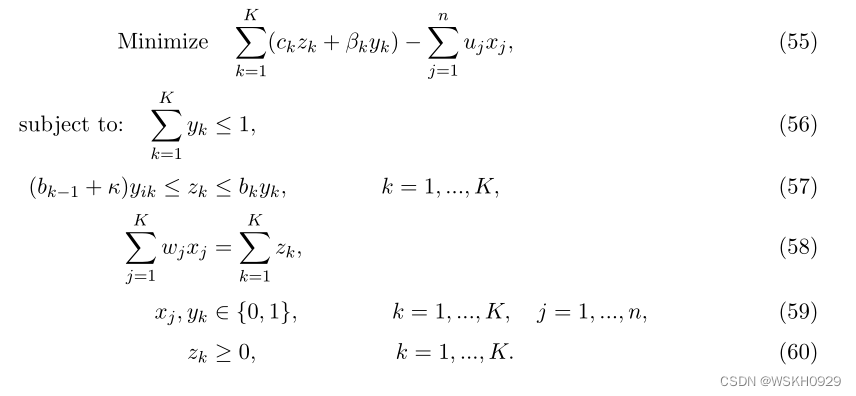
在这里插入图片描述
该模型是显式的，因此没有注释。

注：设 $m$ 为已用容器数目的有效上界，则可按 Desrosiers 和 L¨ ubbecke(2005)的建议计算最佳数值的下界：

在这里插入图片描述

其中，对于迭代 $l$ , $z^l$ 是当前受限主程序的最优值， $σ^∗$ 是定价子问题提供的最小 Reduced Cost 。因此，当 $mσ^∗/z^l$ 小于公差 $\epsilon$ 时，列生成过程停止。

在我们的计算研究中，我们对一些大规模的实例使用了这个停止准则，设置了 $\epsilon = 0.5\%$ ，使用 FFD 启发式后获得的箱数为 $m$ 。

六、Heuristics 启发式方法

在看本节之前，您最好先了解SSP问题及其求解方法：【运筹优化】子集和问题（Subset Sum Problems , SSP）介绍 + 动态规划求解 + Java代码实现

6.1 A constructive subset-sum heuristic 一个构造性的子集和启发式

子集和问题(SSP)要求找到一个项目的子集S，这些项目可以装入单个箱子中，并且使得 $\sum_{j \in S} w_j$ 是最大的。尽管SSP是 NP 困难的，但SSP并不被认为是一个经验困难的问题。这可能解释了它通常嵌入许多箱子包装启发式的事实 (Caprara and Pferschy (2004))。下面的引理强调了SSP和BPPC之间的关系。

引理3：BPPC的特殊情况下，即只需要使用两个箱子就可以装载完物品集合 $J$ 时，BPPC问题可以简化为SSP问题。

证明：设装载最多的仓的总装载量为 $x$ ，则总装载成本为 $Z (x) = f (x) + f (W - x)$ ，其中 $W=\sum_{j \in J} w_j$ 。

因此， $Z^{\prime}(x)=f^{\prime}(x)-f^{\prime}(W-x)$ 。

由于 $f (.)$ 是凹的，且 $x \geq W - x$ ，则 $f^{'} (x) \leq f^{'} (W - x)$ ，因此我们推断 $Z (.)$ 是递减的。

因此，最小化 $Z (.)$ 需要最大化 $x$ 。

这个引理激发了下面的建设性启发式。箱子是按顺序装入的。在每个阶段，求解SSP，从尚未加载最大重量子集的项目中选择不超过bin容量。在后续文章中，我们将把这种启发式方法称为SSP1。

6.2 A local improvement subset-sum heuristic 局部改进子和启发式

引理3的一个直接结果是，任何最优BPPC解满足以下性质。

局部最优条件：从解中选取总装载成本为C的任意一对箱子，求解这两个箱子中所含物品所定义的SSP，则得到的最优解具有相同的装载成本C。

为了推导满足局部最优条件的BPPC的启发式解，我们实现了以下两阶段启发式。在阶段1中，我们调用快速构造启发式来生成初始可行包装。在我们的计算实验中，我们使用了著名的首次拟合递减(FFD)启发式。然而，任何快速BPP启发式方法都可以使用。

在阶段2中，我们迭代地选择一对箱子，解决相关的子集和问题，并在当前解决方案中替换(可能的)优化的箱子对。这个过程不断重复，直到得到一个局部最优解。在实践中，对于实值成本函数的一般情况，我们观察到一个“尾减”效应，即在第一次迭代中快速进展之后，改进在接近尾声时变得极其缓慢。

为了减轻这种影响，我们实现了以下停止标准。假设当前的解决方案由 $m$ 个箱子组成。因此，一个完整的改进迭代周期需要考虑 $m (m - 1) /2$ 个 bin 对。如果连续两个完整周期之间观察到的相对改善小于阈值，则流程将停止。

在我们的实现中，我们将这个值设置为1%。在接下来的内容中，我们将这种启发式方法称为SSP2。

6.3 Worst-case analysis 最坏情况分析

给定一个BPPC实例 $I = (f, J, Q)$ ，我们用 $Z^∗(I)$ 表示最优解的值， $W=\sum_{j \in J} w_j$ 表示累积权值。此外，对于每个启发式 $H$ ，我们用 $Z^H(I)$ 表示启发式解的值， $m_H$ 表示装载的箱子数， $r=\frac{W}{m_H Q}$ 表示箱子装载率。

下列结果对任何启发式函数和任何凹的、可微的、非递减的代价函数都是有效的。

引理4：对于任何启发式 $H$ ，其性能比 $\rho(I)=\frac{Z^H(I)}{Z^*(I)}$ 满足 $\rho(I) \leq \frac{f(r Q)}{r f(Q)}$ 。

证明：如果使用 $m_H$ 箱，则 $Z^H(I)$ 上的有效上界可以通过求解以下优化问题：

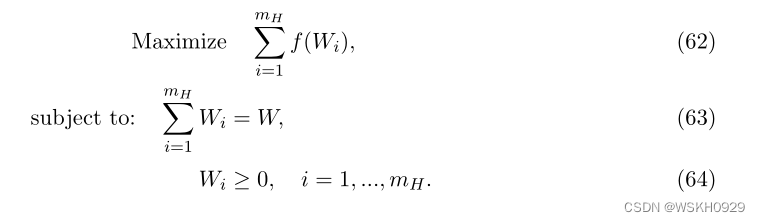
在这里插入图片描述
拉格朗日函数为：

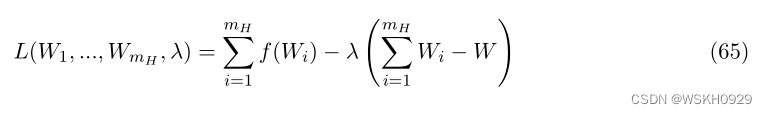
在这里插入图片描述

它的导数是：

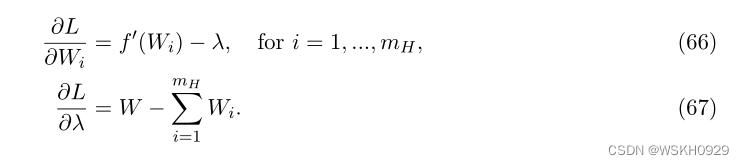
在这里插入图片描述

因此，Karush-Kuhn-Tucker (KKT)条件产生了最优解：

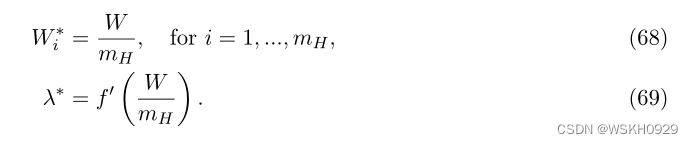
在这里插入图片描述

因此，我们得到：

在这里插入图片描述

另一方面，我们知道：

在这里插入图片描述

因此，将(70)和(71)结合起来，结果如下。

给定由启发式 $H$ 生成的解，我们用 $W_i$ 表示容器 $i$ ： $i = 1,…,m_H)$ 。

假设A ：以下不等式成立：

在这里插入图片描述

显然，这个假设要求启发式永远不会生成一个可以通过将两个箱子合并为一个箱子而得到简单改进的解决方案。在这个温和的假设下，我们可以根据一般的结果得出以下结论。

引理5：对于任何凹非递减函数 $f (.)$ ，满足假设A的任何BPPC启发式 $H$ 的绝对最差情况性能比 $ρ$ 的边界为2，并且对于某些启发式的边界很紧。

证明：由于 $f (.)$ 是非递减的，那么根据引理4，我们有 $\rho \leq \frac{1}{r}$ 。

利用 $H$ 满足假设A的事实，并通过对 $m_H(m_H−1)/2$ 不等式求和，我们得到：

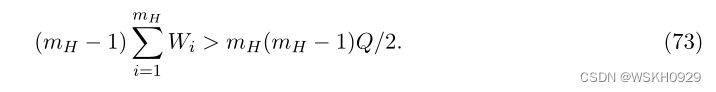
在这里插入图片描述

因此：

在这里插入图片描述

因此， $\frac{1}{2}$ 。因此， $ρ < 2$ 。界限很紧，因为Li和Chen(2006)已经表明，第一拟合(FF)和最佳拟合(BF)启发式都表现出最差情况下的性能比为2。

因此，SSP1的最差情况性能比的上限为2。另一方面，Graham(1972)证明了BPP的SSP启发式最坏情况性能比的下界大于或等于 $\sum_{p=1}^{\infty} \frac{1}{2^p-1} \approx 1.6067$ 。因此，这个下限也适用于SSP1的最差情况性能比。

七、Computational results 计算结果

我们用新生成的加载成本函数扩充BPP实例，构建了一个BPPC测试平台。为了实现这一目标，我们考虑了BPPLIB Delorme等人(2018)的30个实例集。这些集合的主要特征如表1所示。

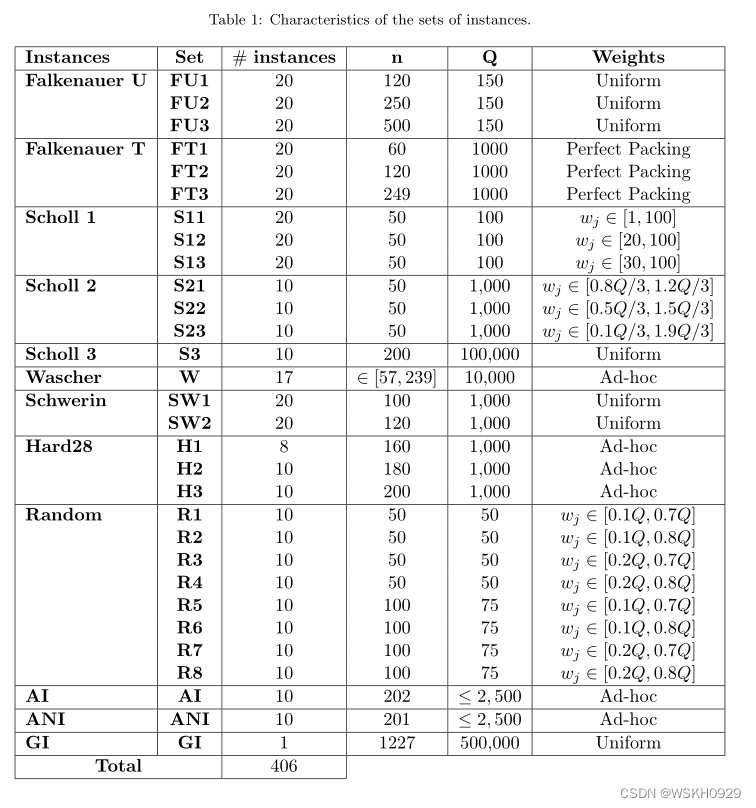
在这里插入图片描述

对于每一组实例，我们考虑两个代价函数:

分段线性函数(PWL)具有四个断点 ${0,Q/3, 2Q/3, Q}$ 和单位代价 ${10,5,1}$ 。
非线性凹函数(NL)定义为 $=\sqrt{Qx}$ 。

因此，我们总共生成了812个实例。在这方面，应该注意的是，不同问题大小、项目权重分布、加载成本函数的组合导致了非常多样化的测试平台。利用 ${0,Q/5, 2Q/5, 3Q/5, 4Q/5, Q}$ 中的6个断点计算内近似。所有下边界和上边界过程用Python 3.8.7编码，列生成算法用CPLEX 20.10实现。所有实验都在一台装有第11代英特尔®酷睿™ i7-1165G7 @ 2.80GHz处理器和16GB RAM的Windows 10机器上运行。

表2和表3分别显示了分段线性代价和非线性代价所获得的结果的摘要。在这两个表中，对于每个下界，标记为GAP的列显示了下界值与最佳启发式值的相对偏差百分比。类似地，对于每个启发式，GAP表示启发式值与最大下界的相对偏差百分比。此外，在标记为M_GAP的列中，我们报告相对的最大百分比。此外，我们在标记为Time和M_Time的列中分别报告平均CPU时间和最大CPU时间(以秒为单位)。

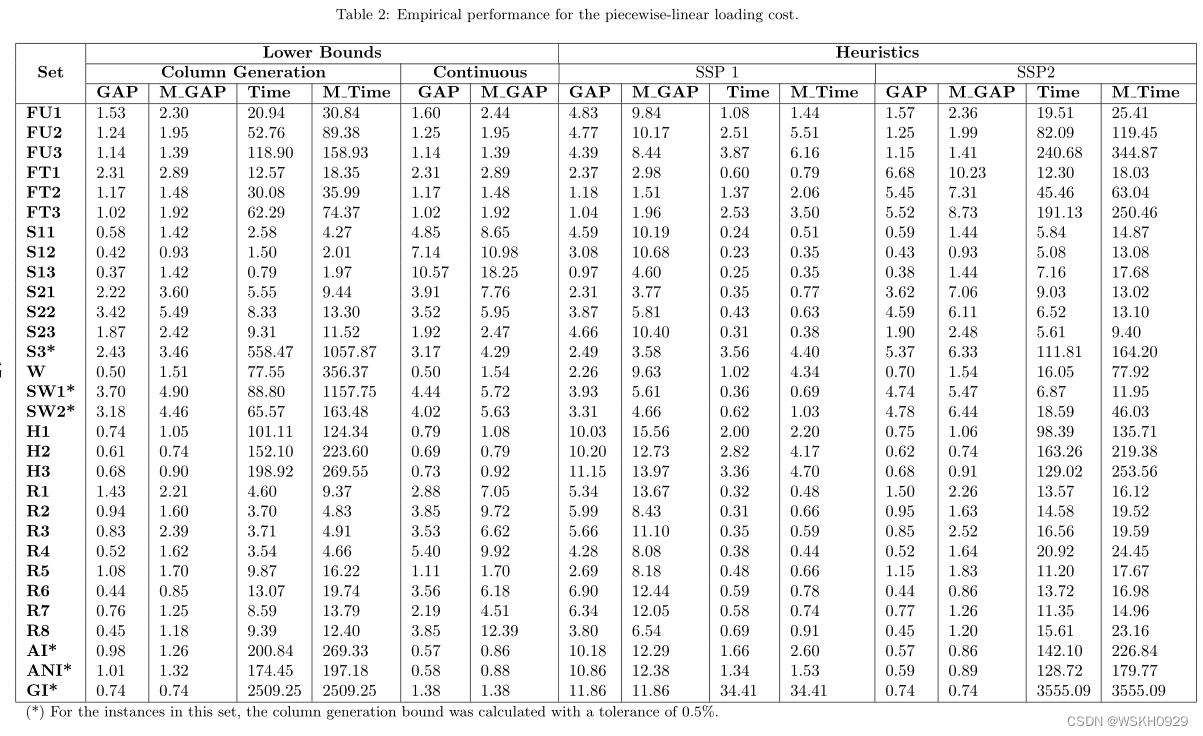
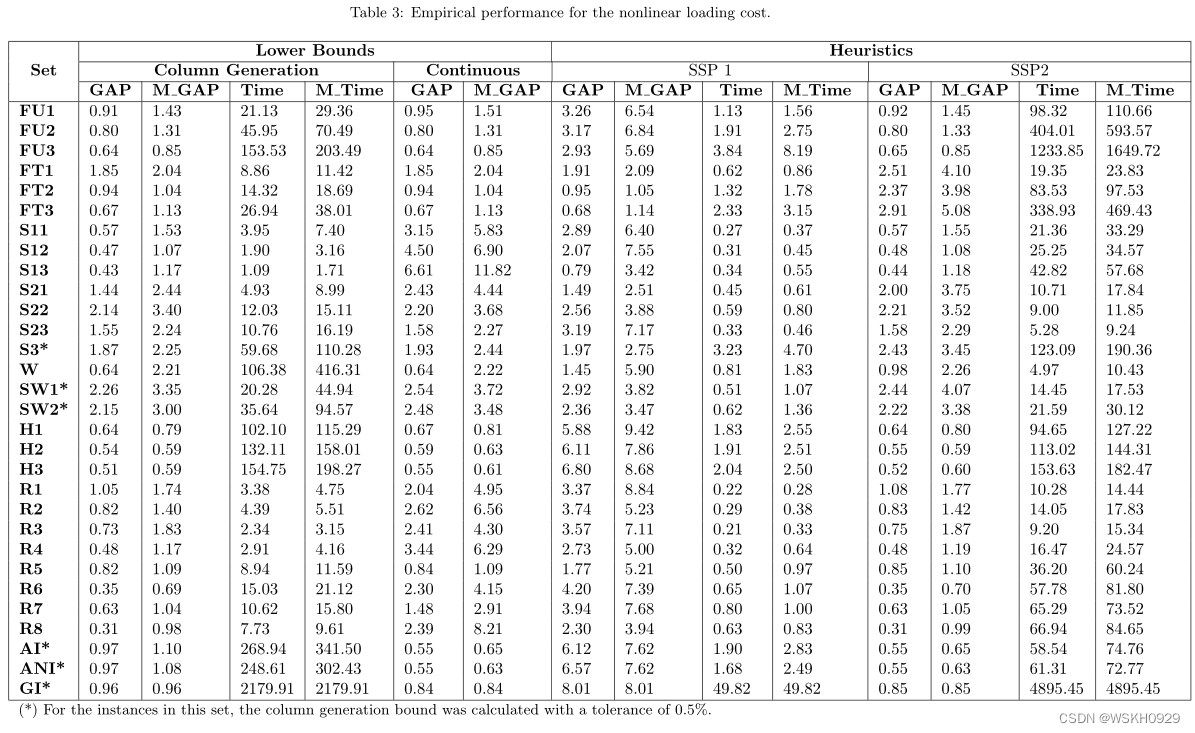
在这里插入图片描述

在这里插入图片描述
看看这些表格，我们可以得出以下结论。

装载成本结构直接影响不同程序的性能。事实上，我们看到所提出的下界和上界过程对于非线性实例比分段线性实例执行得更好。特别地，我们发现SSP2的平均偏差(对所有实例计算)对于非线性实例为1.25%，而对于分段线性实例为2.25%。
尽管它很简单，但连续下界表现得相当好，对非线性实例和分段线性实例的平均偏差分别为1.97%和3.01%。另一方面，列生成界在非线性和分段线性实例中表现出较高的性能，平均偏差分别为0.99%和1.34%。然而，第一个下界所需要的时间可以忽略不计，而第二个下界所需要的时间高达2509.25 s，尽管实现了早停准则。
在几乎所有的问题集中，SSP2始终优于SSP1。SSP1性能更好的少数例外是子集FT1、FT2和FT3的实例，它们的特征是通过三项的完美打包获得实例。总体而言，SSP2在所有812个实例上的平均偏差为1.75%，非线性实例和分段线性实例的最大偏差分别为5.08%和10.23%。当然，SSP2的良好性能导致更长的计算时间，对于最大的实例(有1227个项)几乎达到4895.45秒，而SSP1解决任何实例的时间都不到50秒。

八、Conclusion 结论

本文研究了具有凹形装载代价的一维仓装问题。这个问题通常出现在少于卡车载重的运输服务中，物流公司通常会提供递增折扣。
我们提出了两个下界。第一个是连续松弛问题的最优解。为了在O(1)中计算它，提出了一种封闭形式。第二种是基于大规模集划分公式的问题。通过列代法得到了该公式内近似的LP松弛解。
此外，我们设计了两个基于子集和的启发式算法。第一种是建设性的启发式，通过解决一系列子集和问题来构建可行的解决方案。第二种是局部搜索启发式，通过选择箱对并解决相应的子集和问题，迭代地尝试改进当前的解决方案。
我们证明，在温和的假设下，任何BPPC启发式和任何凹加载代价函数的最差情况性能都以2为界。在这方面，一个值得研究的开放问题是：是否可以为已经知道下界1.6067的子集和启发式推导出更严格的上界。
我们的下界和启发式在文献中的几个BPP实例类上进行了测试。用分段线性函数和非线性函数对这些实例进行了扩展。
总的来说，我们的测试平台包括812个具有广泛多样性特征的实例。最大的实例涉及1227件物品和容量为50万的垃圾箱。
实验表明，所提出的连续下界和建设性启发式方法尽管简单，但在很短的时间内提供了相当紧凑的边界。
另一方面，基于列生成的下界算法和局部搜索启发式算法始终表现出出色的性能。
所提出的下边界和上边界方法的良好性能表明，将它们集成到求解BPPC的精确方法中是一个有前途的研究途径。
此外，我们建议进一步研究具有凹形装载成本的仓装问题的变体。在这方面，二维料仓包装问题和凹装载成本的矢量包装问题似乎特别相关。