常见排序算法总结
目录
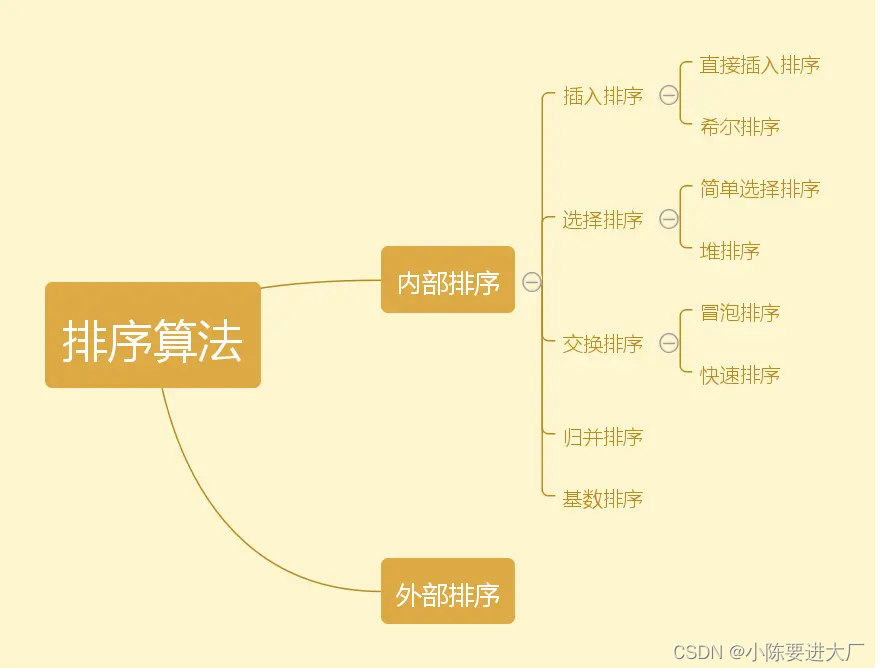
1.直接插入排序
从前往后,每次在前面已经排好序的数组里找到自己的位置并插入;
public void sort(int[] arr) {
for(int i=0;i<arr.length;i++){
for(int j=i-1;j>=0;j--){
if(arr[j]>arr[j+1]) {
swap(arr,j,j+1);
}else{
break;
}
}
}
}2.希尔排序
从len/2的间隔开始每次折半,每一次的排序,按照间隔将间隔特定距离的数按照直接插入排好;
public void sort(int[] arr,int k) {
if(k==0) return;
for(int j=k;j<arr.length;j+=k){
for(int q=j-k;q>=0;q-=k){
if(arr[q]>arr[q+k]){
swap(arr,q,q+k);
}
}
}
sort(arr,k/2);
}3. 简单选择排序
每次选择未排序中的最小值,插入到已经排序的数列的末尾
public void sort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
int index=getMinIndex(arr,i);
swap(arr,i,index);
}
}
private int getMinIndex(int[] arr, int i) {
int min_index=i;
int min=arr[i];
for (int j = i; j <arr.length; j++) {
if(arr[j]<min){
min_index=j;
min=arr[j];
}
}
return min_index;
}4. 堆排序
利用数组实现最小堆,最大堆,注意最大堆最小堆的开头第一个节点序号只能为1不能为0;
public void sort(int[] arr) {
List<Integer> res=new ArrayList<>();
int k=0;
while(k<arr.length){
for(int i=arr.length-k;i>1;i--){
sort(arr,i);
}
res.add(arr[0]);
swap(arr,0,arr.length-1-k);
k++;
}
int j=0;
for(int i=0;i<arr.length;i++){
arr[j++]=res.get(i);
}
}
public void sort(int[] arr, int j) {
while(j>1){
int k=j/2*2;
if(k+1<=j && getNode(arr,k+1)<getNode(arr,k)){
k=k+1;
}
if(k<=j && getNode(arr,j/2)<getNode(arr,k)){
k=j/2;
}
swap(arr,j/2-1,k-1);
j/=2;
}
}
private int getNode(int[] arr,int i) {
return arr[i-1];
}5.冒泡排序
依此交换相邻两个元素使得前一个元素小于后一个,如果某一趟没有交换则结束;
public void sort(int[] arr) {
for(int j=1;j<=arr.length-1;j++){
boolean flag=false;
for (int i = arr.length-1; i >=1; i--) {
if(arr[i-1]>arr[i]){
swap(arr,i-1,i);
flag=true;
}
}
if(!flag) break;
}
}6. 快速排序
选定一个基准值,左边的小于基准值,右边的大于基准值,基准值插中间;
private void sort(int[] arr, int i, int j) {
if(i>=j) return ;
int index=arr[i];
int left=i,right=j;
while(left<right){
while(left<right && arr[right]>=index){
right--;
}
if(left<right){
arr[left]=arr[right];
left++;
}
while(left<right && arr[left]<=index){
left++;
}
if(left<right){
arr[right]=arr[left];
right--;
}
}
arr[left]=index;
index =left;
sort(arr,i,index-1);
sort(arr,index+1,j);
}7. 2路归并
折半递归,合并折半的两个有序的链表
private void sort(int[] arr,int i,int j){
if(i>=j) return;
int k=(j-i+1)/2;
sort(arr,i,i+k-1);
sort(arr,i+k,j);
merge(arr,i,k,j);
}
private void merge(int[] arr, int i, int k, int j) {
int s1=i,s2=i+k,e1=i+k-1,e2=j;
int [] res=new int[j-i+1];
int q=0;
while(s1<=e1 && s2<=e2){
if(arr[s1]<arr[s2]){
res[q++]=arr[s1];
s1++;
}else{
res[q++]=arr[s2];
s2++;
}
}
while(s1<=e1 ){
res[q++]=arr[s1];
s1++;
}
while(s2<=e2){
res[q++]=arr[s2];
s2++;
}
q=0;
while(i<=j){
arr[i]=res[q];
q++;
i++;
}
}8.基数排序
- 基数排序:通过序列中各个元素的值,对排序的N个元素进行若干趟的“分配”与“收集”来实现排序。
分配:我们将L[i]中的元素取出,首先确定其个位上的数字,根据该数字分配到与之序号相同的桶中
收集:当序列中所有的元素都分配到对应的桶中,再按照顺序依次将桶中的元素收集形成新的一个待排序列L[ ]
对新形成的序列L[]重复执行分配和收集元素中的十位、百位...直到分配完该序列中的最高位,则排序结束
9.数据测试
public static void main(String[] args) {
int n=10000;
int[] arr=new int[n];
int[] brr=new int[n];
for(int i=0;i<n;i++){
arr[i]= new Random().nextInt(1000);
brr[i]=arr[i];
}
// System.out.println(Arrays.toString(arr));
// System.out.println(Arrays.toString(brr));
Arrays.sort(arr);
// System.out.println(Arrays.toString(arr));
// SortMath s= new DirectInsert();
// SortMath s= new XierSort();
// SortMath s= new DirectChoose();
// SortMath s= new DuiSort();
// SortMath s= new BoomSort();
// SortMath s= new RapidSort();
// SortMath s=new CombbineSort();
// SortMath s=new BaseSort();
SortMath []t=new SortMath[]{ new DirectInsert(), new XierSort(),
new DirectChoose(),new DuiSort(),
new BoomSort(),new RapidSort(),
new CombbineSort(),new BaseSort()};
TreeMap<Long,String> te=new TreeMap<>();
for(SortMath p:t){
long start=System.currentTimeMillis();
SortMath s=p;
s.sort(brr);
long end =System.currentTimeMillis();
System.out.println("排序算法:"+p.getClass().getName());
System.out.println("用时:"+(end-start));
for(int i=0;i<n;i++){
if(arr[i]!=brr[i]){
System.out.println("error");
System.out.println(Arrays.toString(arr));
}
}
System.out.println("correct!!!");
te.put(end-start,p.getClass().getName());
}
for(Long p:te.keySet()){
System.out.println(te.get(p)+"----"+p);
}
}10.算法的稳定性
排序算法的稳定性大家应该都知道,通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下,如果Ai = Aj,Ai原来在位置前,排序后Ai还是要在Aj位置前。
11.表格
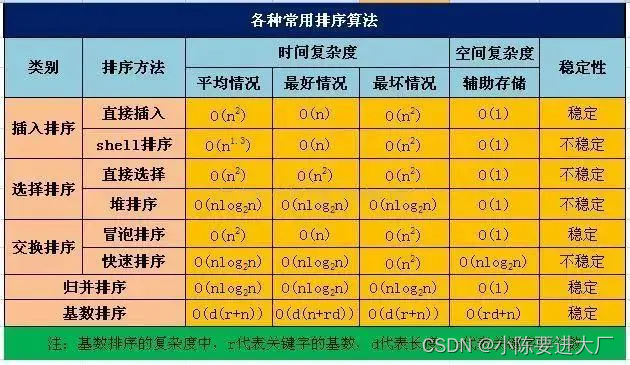
参考:
1. https://baijiahao.baidu.com/s?id=1602011058247698952&wfr=spider&for=pc