《啊哈算法》学习笔记(二)——搜索与图的遍历
搜索与图的遍历
《啊哈算法》在“搜索”前还有两个章节,讲了数据结构中的栈、队列和链表以及枚举算法。这些内容比较浅显,只是简单介绍,这里就不记录了,后续自学数据结构时会提到。这篇把搜索和图的遍历放在一起。
dfs——深度优先搜索
#include <stdio.h>
int a[20][20];//用来存储地图,0为路,1为障碍
int book[20][20];//记录某点是否已走过(在路径上)
int min = 999, way, top;
int n, m;
int end_x, end_y;
struct Stu
{
int x;
int y;
} pos[100];
void dfs(int x, int y, int step)
{
int i;
int next[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//模拟走向右上左下
if (x == end_x && y == end_y)判断是否到达终点
{
if (step < min)
min = step;
way++;
if (way == 1)
printf("找到路了!\n");
for (i = 0; i <= top; i++)//输出路径
{
if (i != 0)
printf("→");
printf("(%d,%d)", pos[i].x, pos[i].y);
}
printf("\n");
}
for (i = 0; i < 4; i++)
{
int tx = x + next[i][0];
int ty = y + next[i][1];
if (tx < 0 || tx >= n || ty < 0 || ty >= m)//是否越界
{
continue;
}
if (a[tx][ty] == 0 && book[tx][ty] == 0)//判断是否走过以及是否为路
{
book[tx][ty] = 1;
top++;
pos[top].x = tx;
pos[top].y = ty;
dfs(tx, ty, step + 1);
top--;
book[tx][ty] = 0;
}
}
}
int main()
{
int i, j;
int start_x, start_y;
printf("请输入地图的行列数:\n");
scanf("%d %d", &n, &m);
printf("请输入地图信息:\n");
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
scanf("%d", &a[i][j]);
printf("请输入起始点和终点坐标:\n");
scanf("%d %d %d %d", &start_x, &start_y, &end_x, &end_y);
pos[0].x = start_x;
pos[0].y = start_y;
book[start_x][start_y] = 1;
dfs(start_x, start_y, 0);
if (!way)//如果没找到一条路
printf("死路一条!\n");
else
printf("共有%d种走法,最短路径需要走%d步\n", way, min);
return 0;
}
dfs算法巧妙的运用递归思想,每一个递归的尽头都是一条路,再附加栈结构存储走过点的坐标,就可以描述路线。大致流程如下:
判断(x,y)是否已到达终点→如果没到达,用next数组遍历在该点的基础上右上左下各点是否能走→对每一个“下一步”判断→是否越界→是否走过/可走→若可走,book数组记录→放入栈内→dfs进入下一步的递归→book数组取消标记,位置信息出栈(top–)
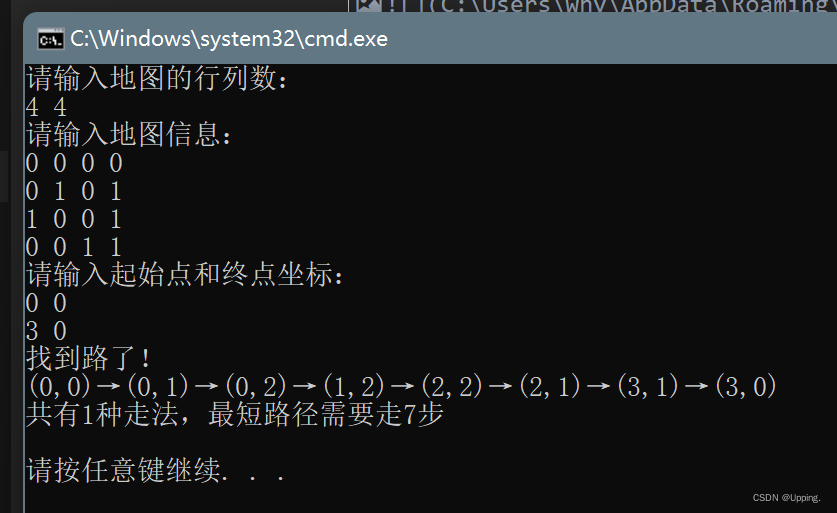
可以输入测试数据得到结果:
bfs——广度优先搜索
#include <stdio.h>
struct Stu
{
int x;
int y;
// int f;
int s;
}; //记录一个点的坐标,并且记录到这个点要多少步,和到该店的父结点要多少步
int main()
{
int i, j;
int start_x, start_y, p, q; //起始点后终点的坐标
struct Stu que[2500]; //构造队列
int head = 0, tail = 0;
int a[51][51] = {0}; //地图信息
int book[51][51] = {0}; //标记已走位置信息
int m, n; //地图的行列数
int next[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; //对应着走向右上左下
int tx, ty; //对应着下一步的坐标
int flag = 0; //判断是否到达终点
printf("请输入地图的行列数:\n");
scanf("%d %d", &n, &m);
printf("请输入地图信息:\n");
for (i = 0; i < n; i++)
{
for (j = 0; j < m; j++)
{
scanf("%d", &a[i][j]);
}
}
printf("请输入起始点和终点的坐标:\n");
scanf("%d %d %d %d", &start_x, &start_y, &p, &q);
que[tail].x = start_x;
que[tail].y = start_y;
// que[tail].f = 0;
que[tail].s = 0; //对队列信息初始化
book[start_x][start_y] = 1; //标记起点已经走过
tail++;
while (head < tail)
{
for (i = 0; i < 4; i++)
{
tx = que[head].x + next[i][0];
ty = que[head].y + next[i][1];
if (tx < 0 || tx > n - 1 || ty < 0 || ty > m - 1)
continue;
if (a[tx][ty] == 0 && book[tx][ty] == 0)
{
book[tx][ty] = 1; //如果(tx,ty)符合要求,就标记这点为走过
que[tail].x = tx; //并将它放入队列中
que[tail].y = ty;
// que[tail].f = head;
que[tail].s = que[head].s + 1;
tail++;
}
if (tx == p && ty == q)
{
flag = 1;
break;
}
}
if (flag == 1)
break;
head++; //当该点能扩展的点都扩展完了head再变化
}
printf("最少走%d步到达终点。\n", que[tail - 1].s);
return 0;
}
bfs与dfs不同的是,它每到一个点,并不是先把一条路走到底,而是先把所在点周围所有的点给判断完,才会再扩散。所以bfs的位置信息并不像dfs一样用栈存储,而是用队列存储。前面提到的“每到一个点”这个点我把它叫做起始点,需要判断它上下左右最临近的4个点,而这个起始点往往在队列中head部位。
判断部分和dfs一样,是否越界,是否为路/已走?如果可走,就把新点放在队尾,并tail++。
图中注释部分,关于que的结构体成员还有一个f,书中说是用f来记录路程信息,如果不输出路线就用不着。但笔者想了半天暂时没有头绪,只觉得有点像链表。另外,如果一个迷宫有多种走法,以上代码并不能输出全部路线,只能输出最简单的那条。而这时我想到一个问题,当碰到一个迷宫问题时,如果有多条路,我们往往就只要最短路径,而上面dfs的代码似乎只能输出全部可行路径,并不能只打印最短路径。
这两个问题暂时搁置,以后碰到再写博客记录。
图的遍历
这一章的内容基本上就是在上一章两种搜索方法的基础上说明了一下图的概念。图就是由一些结点和一些边组成的。边是连接结点之间的通道,但值得注意的是边有单向和双向之分。所以图也分有向图和无向图。其中,有向指的是一条边只能从甲结点到乙结点,而乙结点返回甲结点需要另一条边。无向指的是相邻两节点之间如果有边,他们就是联通的。
本章介绍了图的一种存储方式——邻接矩阵。即
int e[i][j];
这个二维数组的每一个元素为:从左角标到右角标的距离,往往设成一个无穷大的数,说明两者之间无边,而左右角标数值相等时,往往设为0,表示自己到自己零距离。整体框架跟dfs和bfs大同小异,来看一段代码:
#include <stdio.h>
int main()
{
int i, j, n, m, book[101] = {0}, e[101][101]; // book是记录某结点是否走过,e是图的邻接矩阵存储的二维数组
int cur;
int que[10001], head, tail;
printf("请输入图中结点的数量和边的数量:\n");
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++) //初始化二维矩阵
for (j = 1; j <= n; j++)
{
if (i == j)
e[i][j] = 0;
else
e[i][j] = 999;
}
int a, b;
printf("请输入有边的相邻两个结点:\n");
for (i = 1; i <= m; i++)
{
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1;
}
//队列初始化
head = 1;
tail = 1;
que[tail] = 1;
book[1] = 1;
tail++; // que中的结点信息确定后,tail再++
while (head < tail && tail <= n)
{
cur = que[head];
for (i = 1; i <= n; i++)
{
if (e[cur][i] == 1 && book[i] == 0)
{
que[tail] = i;
tail++;
book[i] = 1;
}
}
if (tail > n)
break;
head++;
}
// for (i = 1; i <= n;i++)
// printf("%d ", que[i]);
//以上为初次错误写法,不一定能走完全部结点,如果某一个结点没有相邻的边的话
for (i = 1; i < tail; i++) // i只需要<tail即可,现在的tail是比总结点数多1的
printf("%d ", que[i]);
return 0;
}
代码是图的广度优先遍历,可以注意到,在输入图的信息(有哪些相邻结点有边)时有:
for (i = 1; i <= m; i++)
{
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1;
}
这说明该图为无向图,不管是a到b,还是b到a,都是联通的。
图的遍历只是图的一小个知识点,下一篇博客将介绍图的最短路径算法。
感谢你能看到这里,希望你能有所收获,祝好!