《数字图像处理》第三章学习总结感悟2：直方图处理

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░

一、引言

在2021年6月22日发布《《数字图像处理》第三章学习总结感悟1：灰度变换与空间滤波概念及常用灰度变换方法介绍》之后，老猿就暂停了数字图像处理的学习，而是开始重新学习（本来应该是复习，可是以前的高数知识完全忘光了）高数中的导数、微分、不定积分和定积分相关知识，主要是因为在学习直方图处理中碰到了定积分相关的知识，而这些知识老猿一点概念都没有了。不过总算是过来了，今天我们继续开始图像处理的学习。如果对定积分知识不记得或不知道的，请通过老猿的专栏《人工智能数学基础》进行学习。

二、直方图处理

在这里插入图片描述

2.1、直方图（histogram）处理概述

灰度级（intensity levels）范围为[0,L-1]的数字图像的直方图可以用一个离散函数（discrete function）h(rk)=nk表示（此两处中的k原文是下标k，为了书写简便，没有用下标形式，特此说明，下同），其中rk是第k级灰度值，nk是图像中灰度为rk的像素个数。

假设M和N是图像的行数和列数，乘积MN表示的图像像素的总数，在实践中，常用每个灰度级的像素个数除以MN来归一化直方图（normalized histogram）。因此，归一化后的直方图由p(rk)=nk/MN给出，其中k=0、1、…、L-1，归一化直方图的所有分量之和应等于1。简单地说，p(rk)是灰度级在图像中出现的概率的一个估计。

直方图是多种空间域（spatial domain）处理技术的基础。直方图操作（Histogram manipulation）可用于提供有用的图像统计（image statistics）信息、图像增强（image enhancement）、图像压缩与分割。

直方图在软件中计算简单，而且有助于商用硬件实现，因已成为实时图像处理的一种流行工具。

作为灰度变换的直方图处理的介绍，我们考虑下面的图3.16：

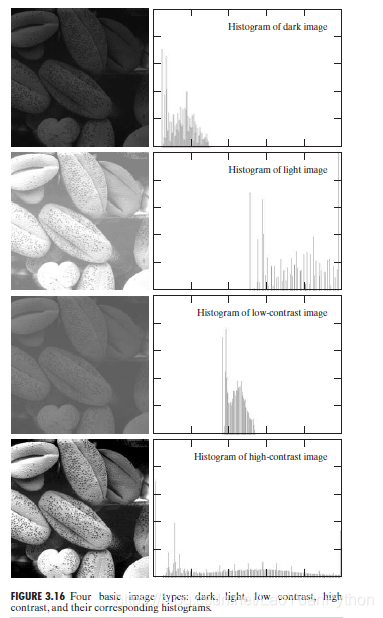
在这里插入图片描述

图3.16是《《数字图像处理》第三章学习总结感悟1：灰度变换与空间滤波概念及常用灰度变换方法介绍》3.5.2节（分段线性变换应用1–对比度拉伸）中的花粉图像（pollen image）。

图3.16所示的以4个基本灰度级为特征的花粉图像：暗图像(dark image)、亮图像（light image）、低对比度图像（low contrast image）和高对比度图像（high contrast image）。图的右侧显示了与这些图像对应的直方图，每个直方图的水平轴对应于灰度值rk，垂直轴对应于值h(rk)=nk，或归一化后的值p(rk)=nk/MN。

因此直方图就可以简单地被看成是对应于rk的h(rk)=nk或p(rk)=nk/MN的图形。

从图3.16可以看出：

在暗图像中，直方图的分量集中在灰度级的低(暗)端
亮图像直方图的分量则倾向于灰度级的高端
低对比度图像具有较窄的直方图，且集中于灰度级的中部。对于单色图像，这意味着暗淡，好像灰度被冲淡了一样
高对比度图像中直方图的分量覆盖了很宽的灰度级范围，而且像素的分布没有太不均匀，只有少量垂线比其他的高许多

直观上,可以得出这样的结论：若一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，则该图像会有高对比度的外观，并展示灰色调的较大变化。最终效果将是一幅灰度细节丰富且动态范围较大的图像。

实际上，仅仅依靠输入图像直方图中的可用信息就可开发出一个变换函数来自动地实现这种效果，在下面的直方图均衡中将介绍与此相关的内容。

直方图处理涉及直方图均衡、直方图匹配、局部直方图处理、图像增强中使用直方图统计等内容，而且涉及相关的数学知识，这部分将分为多篇博文进行介绍，相关内容随着后续的介绍逐渐补充。

2.2、直方图处理博文目录

本文涉及一系列博文，将逐渐更新（其中带星号的为付费专栏文章）：

三、小结

本文及其子系列文章介绍了数字图像处理有关的概念、数学知识以及直方图均衡、直方图匹配、局部直方图处理、图像增强中使用直方图统计等内容，方便详细学习数字图像处理的直方图处理。

更多图像处理请参考专栏《OpenCV-Python图形图像处理》及《图像处理基础知识》的介绍。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《专栏：Python基础教程目录》从零开始学习Python。

如对文章内容存在疑问或需要相关资料，可在博客评论区留言，或关注：老猿Python 微信公号发消息咨询，可通过扫二维码加微信公众号。
在这里插入图片描述

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》；
付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》；
付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录》
付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░

一、引言

二、直方图处理

2.1、直方图（histogram）处理概述

2.2、直方图处理博文目录

三、小结

写博不易，敬请支持：

关于老猿的付费专栏

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░