PyTorch初探：基本函数与案例实践

正文：

        在熟悉了PyTorch的安装和环境配置后，接下来让我们深入了解PyTorch的基本函数，并通过一个简单的案例来实践这些知识。

1. 基本函数

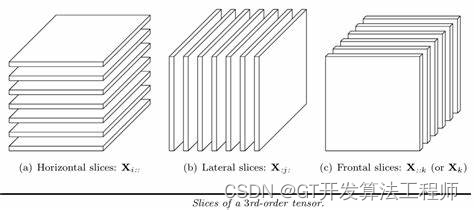
        PyTorch的核心是张量（Tensor），它类似于多维数组，但可以在GPU上运行以加速计算。张量上的操作是构建神经网络层的基础。

 

---

    以下是PyTorch中一些常用的张量操作函数：

• torch.tensor(): 创建一个新的张量。
• torch.ones(), torch.zeros(): 创建全1或全0的张量。
• torch.randn(): 创建一个具有随机数的张量，这些随机数服从均值为0和标准差为1的正态分布（标准正态分布）。
• torch.matmul(): 执行矩阵乘法。
• torch.sum(): 计算张量中所有元素的和。

---

         此外，PyTorch还提供了自动求导机制，这是训练神经网络的关键。通过设置张量的requires_grad属性为True，PyTorch会跟踪对该张量执行的所有操作，以便后续计算梯度。

2. 案例实践：线性回归

        为了演示PyTorch的基本用法，我们将实现一个简单的线性回归模型。线性回归是一种预测模型，其中输出是输入的线性组合。

步骤如下：

• 导入必要的库：

import torch  
import torch.nn as nn  
import torch.optim as optim

• 准备数据：

这里我们使用简单的人工数据来演示。

# 输入数据  
x_data = torch.tensor([[1.0], [2.0], [3.0]])  
# 输出数据  
y_data = torch.tensor([[2.0], [4.0], [6.0]])

• 定义模型：

线性回归模型可以表示为y = wx + b，其中w是权重，b是偏置。

class LinearRegressionModel(nn.Module):  
    def __init__(self):  
        super(LinearRegressionModel, self).__init__()  
        self.linear = nn.Linear(1, 1)  # 输入和输出都是1维的  
  
    def forward(self, x):  
        y_pred = self.linear(x)  
        return y_pred  
  
model = LinearRegressionModel()

• 定义损失函数和优化器：

criterion = nn.MSELoss()  # 均方误差损失  
optimizer = optim.SGD(model.parameters(), lr=0.01)  # 随机梯度下降

• 训练模型：

# 训练周期  
epochs = 100  
  
for epoch in range(epochs):  
    # 前向传播  
    outputs = model(x_data)  
    loss = criterion(outputs, y_data)  
  
    # 反向传播和优化  
    optimizer.zero_grad()  
    loss.backward()  
    optimizer.step()  
  
    # 打印损失  
    if (epoch+1) % 10 == 0:  
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item()}')  
  
# 测试模型  
with torch.no_grad():  
    prediction = model(torch.tensor([[4.0]]))  
    print(f'Prediction after training: {4.0} => {prediction.item()}')

---

• 总结       

• 在这个简单的案例中，我们展示了如何使用PyTorch构建、训练和测试一个基本的线性回归模型。通过这个过程，你应该对PyTorch的基本函数和工作流程有了更深刻的理解在实际应用中，你可能会处理更复杂的模型和数据集，但基本的原理和操作是相似的。