C. Theofanis‘ Nightmare

Theofanis 在入睡前很容易沉迷于各种问题，经常做噩梦。为了解决这个问题，他去看了他的医生 Emix 博士。
在他最近的噩梦中，他有一个大小为 n 的数组 a ，想把它分成非空的子数组，使得每个元素都正好在其中一个子数组中。
例如，数组 [1,−3,7,−6,2,5] 可以划分为 [1][−3,7][−6,2][5] 。
这种分割的塞浦路斯值等于 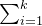 i⋅sumi，其中 k 是我们将数组分割成的子数组的个数，sumi 是第 i 个子数组的和。
这个数组的塞浦路斯值为 [1][−3,7][−6,2][5]=1⋅1+2⋅(−3+7)+3⋅(−6+2)+4⋅5=17 。
Theofanis 想知道任何数组划分的最大塞浦路斯值是多少。
数组 b 是数组 a 的子数组，如果 b 可以从 a 中通过删除开头的几个(可能是零个或全部)元素和结尾的几个(可能是零个或全部)元素得到。特别地，一个数组是它自身的一个子数组。

输入
第一行包含一个整数 t ( 1 ≤ t ≤ 1e4 ) - 测试用例的数量。
每个测试用例由两行组成。每个测试用例的第一行包含一个整数 n (1 ≤ n ≤ 1e5) - 数组的大小。
第二行包含 n 个整数 a1,a2,…,an (−1e8 ≤ ai ≤ 1e8) - 数组的元素。
保证所有测试用例的 n 之和不超过 2e5 。

输出
为每个测试用例打印一个整数，即数组 a 的最大塞浦路斯值。

Input
4
6
1 -3 7 -6 2 5
4
2 9 -5 -3
8
-3 -4 2 -5 1 10 17 23
1
830

Output
32
4
343
830

注：
在第一个测试案例中，为了得到塞浦路斯的最大值，我们将数组分成 [1][−3][7][−6][2][5] ，这样就得到了：

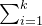 i⋅sumi=1⋅1+2⋅(−3)+3⋅7+4⋅(−6)+5⋅2+6⋅5=32
同样，在第二个测试用例中，我们将数组分成 [2][9,−5,−3] ，得到 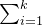 i⋅sumii=1⋅2+2⋅(9+(−5)+(−3))=4 。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e6+10;
int n;
int a[N],p[N];
vector <int> ans;
void solve()
{
    cin>>n;
    for (int i=1;i<=n;i++) cin>>a[i];
    ans.clear();
    int sum=0;
    int res=0;
    for (int i=n;i>0;i--)
    {
        sum +=a[i];
        res +=a[i];
        if (sum>0||i==1)
        {
            ans.push_back(res);
            res=0;
        }
    }
    reverse(ans.begin(),ans.end());
    sum=0;
    for (int i=0;i<ans.size();i++) sum +=ans[i]*(i+1);
    cout<<sum<<endl;
}
signed main()
{
    ios;
    int T=1;
    cin>>T;
    while (T--) solve(); 
    return 0;
}