Pytorch的BN层使用详解
前提知识
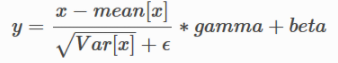
BN层包括mean var gamma beta四个参数,。对于图像来说(4,3,2,2),一组特征图,一个通道的特征图对应一组参数,即四个参数均为维度为通道数的一维向量,图中gamma、beta参数维度均为[1,3]
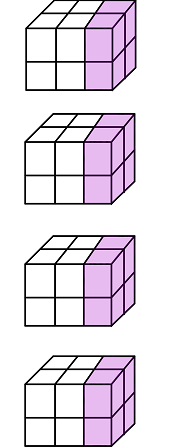
其中gamma、beta为可学习参数(在pytorch中分别改叫weight和bias),训练时通过反向传播更新;
而running_mean、running_var则是在前向时先由X计算出mean和var,再由mean和var以动量momentum来更新running_mean和running_var。所以在训练阶段,running_mean和running_var在每次前向时更新一次;在测试阶段,不用再计算均值方差,则通过net.eval()固定该BN层的running_mean和running_var,此时这两个值即为训练阶段最后一次前向时确定的值,并在整个测试阶段保持不变。
class torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True)
nn.BatchNorm2d(self, num_features, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)
1d
参数:
num_features: 来自期望输入的特征数,C from an expected input of size (N,C,L) or L from input of size (N,L)
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
momentum:滑动平均的参数,用来计算running_mean和running_var。默认为0.1。
track_running_stats,是否记录训练阶段的均值和方差,即running_mean和running_var
affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数。
输入:(N, C)或者(N, C, L)
输出:(N, C)或者(N,C,L)(输入输出相同)
在每一个小批量(mini-batch)数据中,计算输入各个维度的均值和标准差。gamma与beta是可学习的大小为C的参数向量(C为输入大小)
2d
num_features: 来自期望输入的特征数,C from an expected input of size (N,C,H,W)
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
momentum: 动态均值和动态方差所使用的动量。默认为0.1。
affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数,表示weight和bias将被使用
输入:(N, C,H, W) 输出:(N, C, H, W)(输入输出相同)
BN层的状态包含五个参数:
weight,缩放操作的γ gamma。
bias,缩放操作的β beta。
running_mean,训练阶段统计的均值,测试阶段会用到。
running_var,训练阶段统计的方差,测试阶段会用到。
num_batches_tracked,训练阶段的batch的数目,如果没有指定momentum,则用它来计算running_mean和running_var。一般momentum默认值为0.1,所以这个属性暂时没用。
weight和bias这两个参数需要训练,而running_mean、running_val和num_batches_tracked不需要训练,它们只是训练阶段的统计值。
running_mean running_var的计算
在训练时,BN层计算每次输入的均值与方差,并进行移动平均。移动平均默认的动量值为0.1。初始值running_mean=0.running_var=1
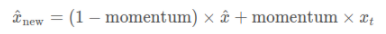
参数更新是以差分的形式进行的,xt代表新一轮batch产生的数据,x^代表历史数据,这个参数越大,代表当前batch产生的统计数据的重要性越强。0.1表示当前batch统计数据占0.1.
对于此处,可表示为:
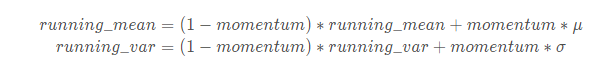
在推理时,训练求得的均值/方差将用于标准化验证数据。
code 验证
gamma beta 分别针对 2个【5 5】的矩阵进行计算。
import torch
import torch.nn as nn
m = nn.BatchNorm2d(2, affine=False)
m1 = nn.BatchNorm2d(2, affine=True)
input = torch.randn(1,2,5, 5)
input = torch.tensor([[[[ 0.92767, 0.56841, -1.68725, -0.01806, 1.31190],
[-0.95227, 1.52581, -1.21351, 0.06448, 2.72040],
[-0.67488, 0.83880, -2.02831, -0.28432, -0.43458],
[-1.96451, -0.15065, -1.87039, 0.13661, 0.25373],
[-0.59261, 1.09675, -0.00749, -0.63954, -1.72408]],
[[-1.04556, -0.07648, -0.42020, 0.06401, -1.15629],
[ 0.77445, -0.23579, -1.26846, -0.09803, 1.07262],
[-2.15755, -0.77489, 0.50311, 0.22077, 0.93678],
[ 0.82926, -0.04959, -0.42568, 0.58730, 1.63708],
[ 0.92501, 1.85740, 0.96766, 0.71574, -0.62078]]]])
output = m(input)
print(input, '\n',output,'\n',output1)
print(m.weight)#None
print(m.bias) #None
print(m1.weight) #1
print(m1.bias) #0
print(m1.running_mean) # init_mean=0,init_var=1
print(m1.running_var)#0.1 更新
running_mean_init=m1.running_mean
running_var_init=m1.running_var
print("输入的第一个维度:")
print(input[0][0]) #这个数据是第一个3*4的二维数据
#求第一个维度的均值和方差
firstDimenMean=torch.Tensor.mean(input[0][0])
firstDimenMean # -0.19192
firstDimenVar=torch.Tensor.var(input[0][0],True) #false表示贝塞尔校正不会被使用#True BN层默认的是用的贝塞尔验证 tensor(1.45355) False:tensor(1.39540)
firstDimenVar # 1.3954
output1 = m1(input)
print(firstDimenMean)
print(firstDimenVar)
print(m1.running_mean) # init_mean=0,init_var=1
print(m1.running_var)#0.1 更新# 验证更新runing-mean var的计算,每计算一次BN,就会更新一次
running_mean_update=running_mean_init.numpy() *0.9+0.1*firstDimenMean.numpy()
running_var_update =running_var_init.numpy()*0.9 + 0.1*firstDimenVar.numpy()
batchnormone=((input[0][0][0][0]-firstDimenMean)/(torch.pow(firstDimenVar,0.5)+m1.eps))*m1.weight[0]+m1.bias[0]
print(batchnormone)
print(output1[0][0][0][0])
上面计算方差时有一个贝塞尔校正系数,具体可以通过如下链接参考:https://www.jianshu.com/p/8dbb2535407e
从公式上理解即在计算方差时一般的计算方式如下:
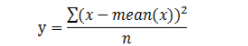
通过贝塞尔校正的样本方差如下:
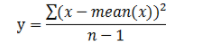
目的是在总体中选取样本时能够防止边缘数据不被选到。详细的理解可以参考上面的链接。