【数据结构】分治策略

现场保护和现场恢复

不要尝试间接
要使用直接递归（自己调用自己）

分治策略

分治法解决问题有以下四个特征：

1. 该问题的规模小到一定程度就容易解决。
2. 把大问题分解成小问题，是将问题的规模变小，而不是将问题变小
3. 使用小规模的解，可以合并，该问题原规模的解
4. 该问题所分解的各个子模块是相互独立的。

分治法步骤:

在分治策略中递归地求解一个问题，在每层递归中有如下解决步骤：
分解：递归地求解子问题，子问题地形式与原问题一样，只是规模更小。
解决：递归地求解子问题，如果子问题地规模足够小，则停止递归，直接求解
合并：将小规模地解组合成原规模地解

递归函数分为 递推和递归两个过程
每当调用发生：就要分配新的栈帧（形参数据，现场保护，局部变量）；而与普通函数调用不同，由于递推是一个逐层调用的过程，因此存在一个连续的分配栈帧的过程，直至遇到递归终止条件时，才开始回归，这时才会释放栈帧空间，返回到上一层，直到返回到主调函数。

• 简单的函数调用过程：
  

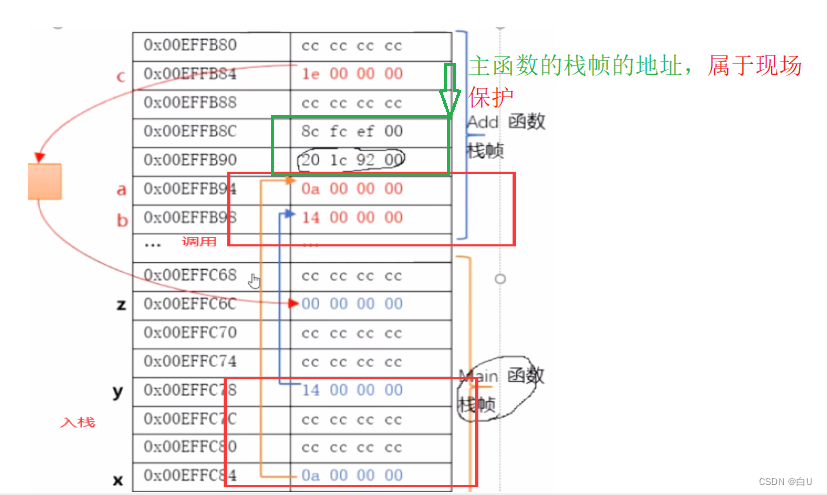
递归：

空间复杂程度位S（n）,每次都要开辟栈帧
必要的情况才使用递归（如树形）
不存在死递归的概念（因为栈帧基本就1M,不断开辟栈帧，资源就损耗完了）
循环占用的cpu资源。因此存在死循环。

解决以下问题：

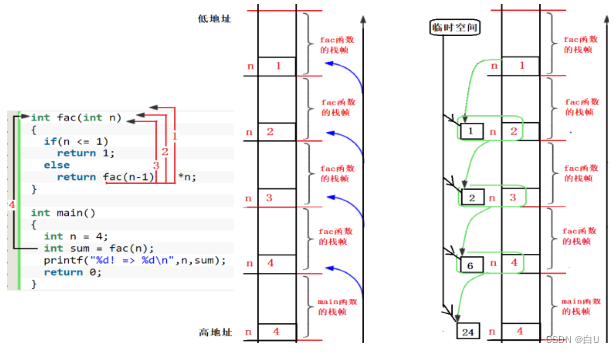
下面程序：

倒序输出整数

Print(int n )
   {
    if(n != 0)
    {                         ----->
         printf("%d ",n%10);  5，4，3，2，1
           Print(n/10);   1235
                          123
                          12
                          1 
                          0  开始回归
                           printf("%d ",n%10);
           Print(n/10); 
           printf("%d ",n%10);1，2，3，4，5
                                   <----
    }
    return;
  }

求最大公约数（递归和非递归）

int fun(int a, int b)
{       //求最大公约数
	if (b != 0)   //退出递归的条件
	{
	    return fun(b,a%b); 
	}  
	return a;
	
}
int fun1(int a, int b)
{       //求最大公约数
	while (b != 0)   
	{
	     int c  = a%b;
	     a = b;
	     b = c;
	     	}  
	return a
}

错误1：

菲波那切数列

后一个数为前两个之和。
打印：

int main()
{
   const int n = 10;
   int arr[n] = {1,1};
   for(int i =2;i<n;i++)
   {
    arr[i] = arr[i-1]+arr[i-2];
   }
}

非递归：

int fac(int n)
{
   int  a = 1,b=1,c=1;  //当n<=3的时候，打印的值均为1也就是前两位
   for(int i = 3;i<=n;i++)
   {
      c = a+b;
      a = b
      b =c;
   }
   return c;
}

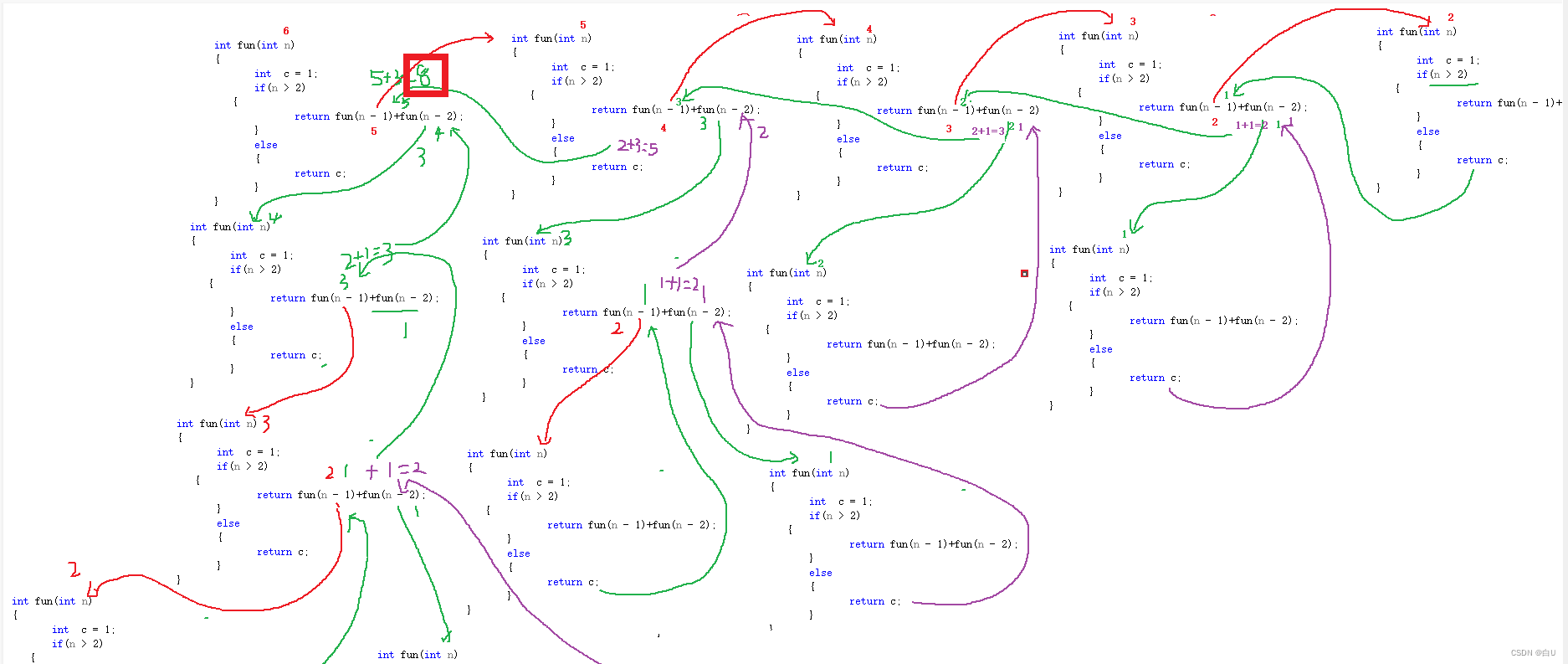
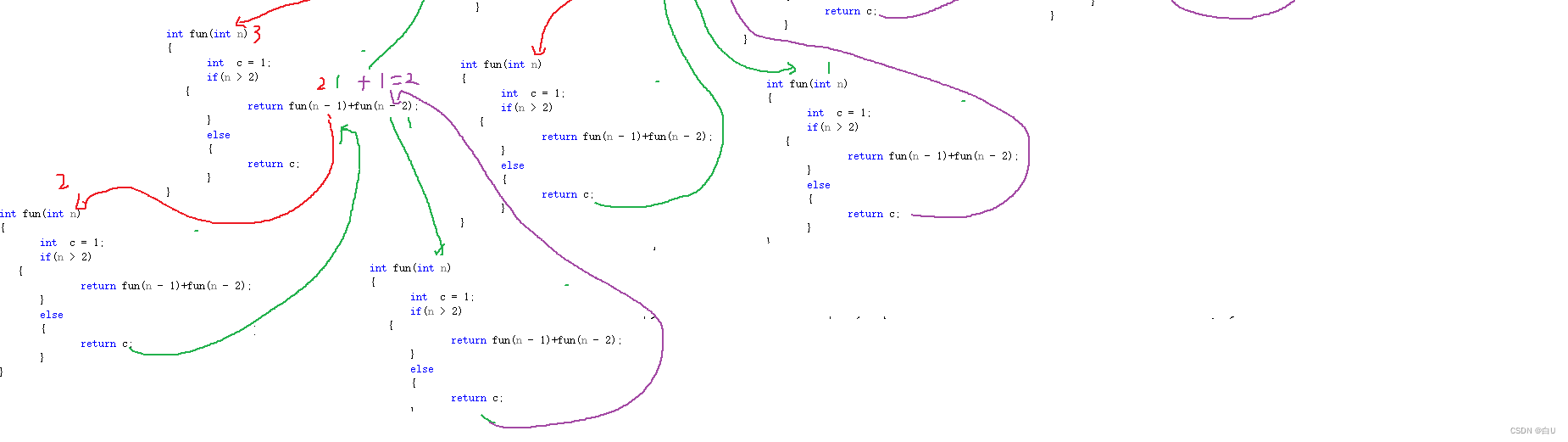
递归：
时间复杂程度：2^n ，跑法是一颗二叉树。
空间复杂程度最大深度是S(n) 。因为递推时开辟栈帧，回归时，销毁栈帧

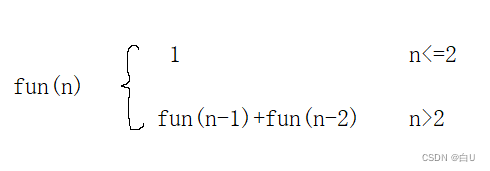
1.判断退出条件
2.分析最后需要的结果

int fac(int n) 
{
	int  c = 1;
	if(n > 2)
   {
		return fun(n - 1)+fun(n - 2);
	}
	else
	{
		return c;
	}
    
	
}

查询：递归和非递归(边界检查)
递归

int FindValue(int* br, int n, int val)
{
	//assert
	int pos = n-1;
	if(pos >= 0 && br[pos] != val  )
	{
		return  FindValue(br,pos,val);
	}
	return pos;
}

非递归

int FindValue(int* br, int n, int val)
{
	//assert
	int pos = n-1;
	if(pos >= 0 && br[pos] != val  )
	{
		pos++;
	}
	return pos;
}

递归：

int FindValue(int* br, int n, int val)
{
	//assert
	//n<1 比 n<=0要好，因为这里的n是规模，1—n的数，而<=0，又有下标的含义
	if (n < 1&& br[n-1] != val)
	{
		return n-1;
	}
	return  FindValue(br, n-1, val);
}

二分查询：（要求数据是有序的，并且数据在内存中的存储是连续的）
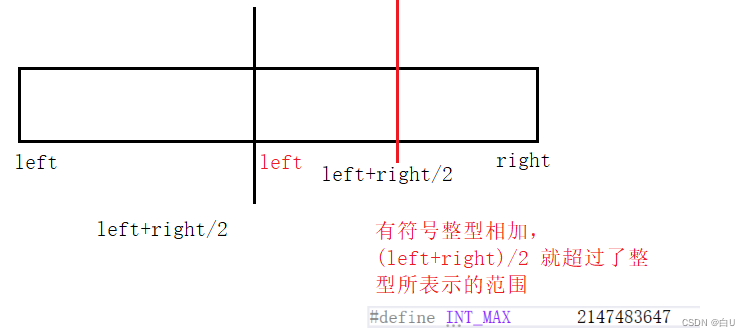
如果数据量小不用考虑下面问题，数据量大，必须考虑下面问题。
所以采用（right-left）/2 + left
例如 1，2，3，4，5 ,6，7，8，9 (8-0)/2 = 4 4+0 = 4，即4号下标
由于存放是以2进制存放，所以左移一位，就相当于除以二
(（right-left）>> 1) +left

int BinaryFind_Value(int *br,int len,int val)
{
  //assert
	int left = 0, right = len - 1;
	int pos = -1;
	int mid = -1;
	while (left < right)
	{   //如果是left+right/2
		mid = (right - left) / 2 + left;
		        //(right - left) >>1 + left;
		if (br[mid] < val)
		{
			left = mid + 1;
		}
		else if(br[mid] > val)
		{
			right = mid; //mid不能加一，因为left<right
			                  //加一有最右边的元素访问不到。
		}
		else
		{
			pos = mid;
			break;
		}
	}
	return pos;
}

• int ar[] = {11 ,11, 11, 11, 11, 11, 12, 12, 13, 14, 15}
  查最左边的11
  

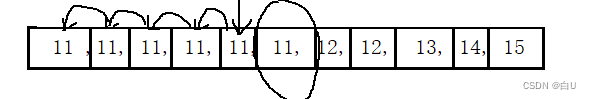
int BinaryFind_Value(int* br, int len, int val)
{
	//assert
	int left = 0, right = len - 1;
	int pos = -1;
	int mid = -1;
	while (left <= right)
	{   //如果是left+right/2
		mid = (right - left) / 2 + left;
		//(right - left) >>1 + left;
		if (br[mid] < val)
		{
			left = mid + 1;
		}
		else if (br[mid] > val)
		{
			right = mid - 1; //mid不能加一，因为left<right
							  //加一有最右边的元素访问不到。
		}
		else
		{                              //可以比较下一个标的值
			while (mid > left && br[mid -1 ] == val)
			{
				//pos = mid;  每次都赋值，浪费时间
				mid--;
			}
			pos = mid;
			break;
		}
	}
	return pos;
}

求ar[1,2,3,]所有子集
ar[0,0,0,0]
0,0,0,1
0,0,1,0
0,0,1,1
…
1,1,1,1
如何降时间复杂程度?