数据结构和算法（五）树（二叉树、满二叉树、完全二叉树、二叉搜索树）

二叉树

二叉树：

二叉树是每个结点最多有两个子树的树结构

满二叉树：

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

完全二叉树：

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

二叉搜索树：

满足“任意结点x,左子树结点值最大不超过x,右子树结点值最小不低于x” 的二叉树。

1、构建

public class Tree {
    private int key; // 结点内容

    private Tree left; // 左子结点

    private Tree right; // 右子结点

    private Tree parent; // 父结点

    private Tree root; // 根结点
    
    // 省略get/set
}

2、插入

通过遍历，找到父结点（从根结点开始），然后在设置是父的左子还是右子

private void insert(Tree tree) {
    Tree x = this.root;
    while (x != null) {
        if (tree.key < x.key) {
            if (x.left == null) {
                break;
            } else {
                x = x.left;
            }
        } else {
            if (x.right == null) {
                break;
            } else {
                x = x.right;
            }
        }
    }
    tree.parent = x;
    if (x == null) {
        this.root = tree;
    } else if (tree.key < x.key) {
        x.left = tree;
    } else {
        x.right = tree;
    }
}

3、最大值和最小值

根据二叉搜索树的概念，左子树的值小于右子树的值。所以，最小值就是：左子树的左子树的左子树…；最大值就是右子树的右子树的右子树…

// 值最小的结点
private Tree minimum(Tree x) {
    while (x.left != null) {
        x = x.left;
    }
    return x;
}

// 值最大的结点
private Tree maximum(Tree x) {
    while (x.right != null) {
        x = x.right;
    }
    return x;
}

4、遍历

命名规则：按根结点输出的顺序

中序遍历：输出的子树根的值位于左子树的值和右子树的值之间

先序遍历：输出的根的值在左右子树的值之前

后序遍历：输出的根的值在左右子树的值之后

图解（中序遍历）[图片出处网络，侵删]：

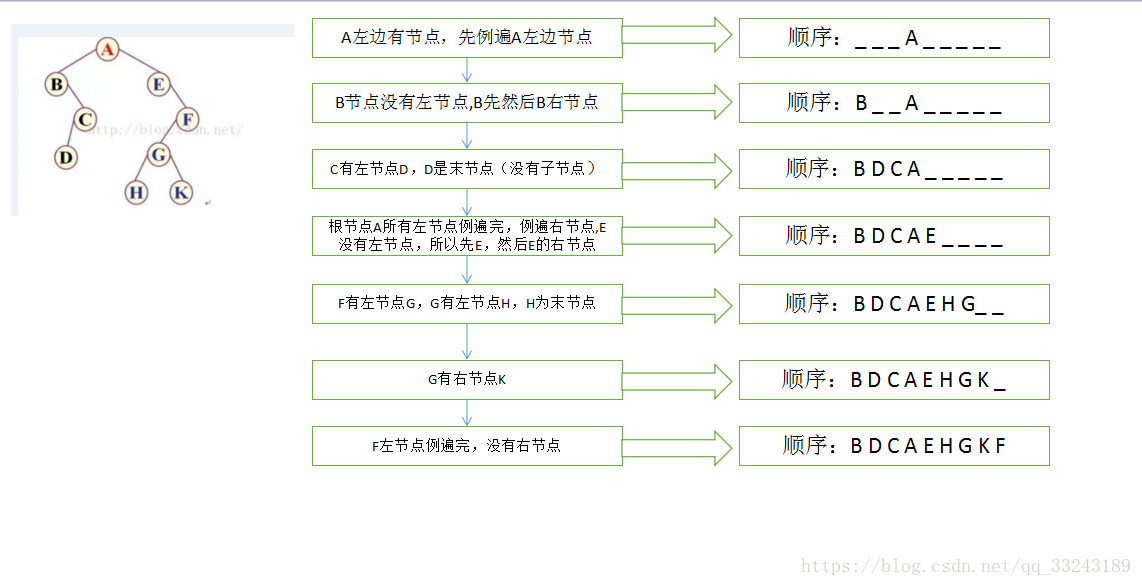
中序遍历

private static void inorder(Tree x) {
    if (x != null) {
        inorder(x.left);
        System.out.print(x.key + ", ");
        inorder(x.right);
    }
}

前序遍历

private static void preorder(Tree x) {
    if (x != null) {
        System.out.print(x.key + ", ");
        preorder(x.left);
        preorder(x.right);
    }
}

后序遍历

private static void postorder(Tree x) {
    if (x != null) {
        postorder(x.left);
        postorder(x.right);
        System.out.print(x.key + ", ");
    }
}

5、搜索

搜索比较简单，从树根开始查找，遇到结点，比较结点值和搜索的值，两值相等，搜索中止。如果查找的值小于结点的值，则查找的值在结点的左子树，继续在左子树重复上述查找动作。

private static Tree search(Tree x, int key) {
    while (x != null && x.key != key) {
        if (x.key > key) {
            x = x.left;
        } else {
            x = x.right;
        }
    }
    return x;
}

6、删除

设要删除的结点为z
（1）如果z没有孩子结点，用null替代z;
（2）如果z有且只有一个孩子结点，将孩子结点替代z;
（3）如果z有两个孩子结点。我们需要查找一个后继y，它需要满足以下两个条件：
a）y位于右子树中；
b）y没有左孩子；
如果y是z的右孩子，直接用y替换z,并留下y的右孩子。
如果y在z右子树，但不是右孩子。先用y的右孩子替换y,然后用y替换z。

private void delete(Tree z) {
    if (z.left == null) {
        transplant(z, z.right);
    } else if (z.right == null) {
        transplant(z, z.left);
    } else {
        Tree y = minimum(z.right);
        if (y.parent != z) {
            transplant(y, y.right);
            y.right = z.right;
            y.right.parent = y;
        }
        transplant(z, y);
        y.left = z.left;
        y.left.parent = y;
    }
}
// 用v子树替代u子树
private void transplant(Tree u, Tree v) {
    if (u.parent == null) {
        this.root = v;
    } else if (u == u.parent.left) {
        u.parent.left = v;
    } else {
        u.parent.right = v;
    }
    if (v != null) {
        v.parent = u.parent;
    }
}

7、扩展（力扣1038 从二叉搜索树到更大和树）

如果您执行了上面的中序遍历代码，会发现中序输出是正序的（从小到大）。有正序就有倒序，我们改下代码，就成倒序了。

private static void inorder2(Tree x) {
    if (x != null) {
        inorder2(x.right);
        System.out.print(x.key + ", ");
        inorder2(x.left);
    }
}

力扣上有一题，正好可以用到这个反向中序。

1038. 从二叉搜索树到更大和树
给出二叉搜索树的根节点，该二叉树的节点值各不相同，修改二叉树，使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

示例：

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
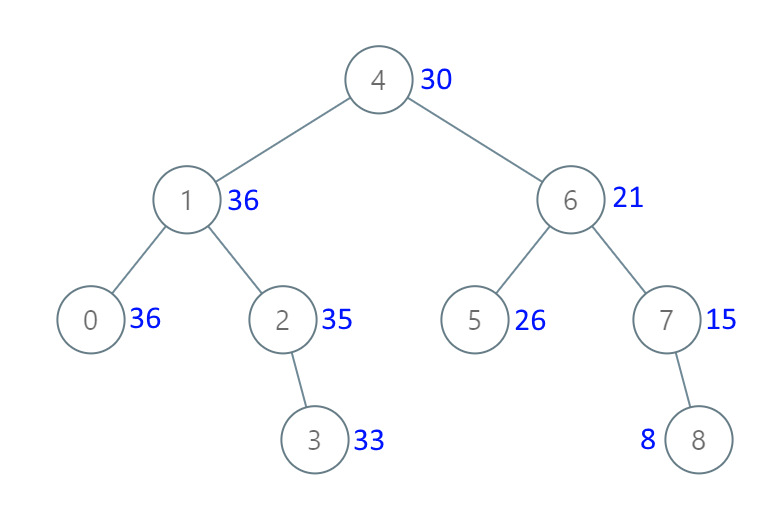
在这里插入图片描述
解题：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int sum = 0;
    public TreeNode bstToGst(TreeNode root) {
        if (root != null) {
            bstToGst(root.right);
            sum += root.val;
            root.val = sum;
            bstToGst(root.left);
        }
        return root;
    }
    
}

[1] 《算法导论》机械工业出版社
[2] 力扣（LeetCode）https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree