简单的递归思想： gcd（最大公因数）+hanoi（汉诺塔）+quicksort（快排）

目录

一、gcd（求最大公因数）

二、hanoi（描述汉诺塔）

三、quicksort（快排）

上次博客本是说这周分享算法的，后来还是想先分享一下递归思想。递归在编程学习中可谓是无处不在，计算机的所有运算拆分开都是递归。比如1+2，可以拆成1+（1+1），同理，所有的加减乘除都可以拆成1+1的式子，这就是递归。给一个拆分的路径，不断地将一个式子递归拆分成一个个小式子，化繁为简。

下面我们用三个经典递归（gcd，hanoi，quicksort）来走进这种思想。

一、gcd（求最大公因数）

求最大公因数，不得不提的就是辗转相除法，也叫欧几里得算法。具体操作：用两数中的较大数除以较小数，之后以除数作被除数，余数作除数，不断相除，以致最后一次余数等于零，此时除数位上的数就为原来两个数的最大公因数。

拿一个具体的例子来说：求20与12的最大公因数。

第一步：20%12==1......8

第二步：12%8==1......4

第三步：8%4==2......0

此时余数已为0，所以20与12的最大公因数为除数位置上的4，即gcd(20,12)==4、

那么用代码如何去实现呢？根据直观感受，我们可以这样写：

int gcd(int x, int y)//自定义函数，确保两数中，x>y
{
	int yu = x % y;//余数
	while (yu)//循环至余数等于零
	{
		x = y;
		y = yu;
		yu = x % y;
	}
	return y;//此时的除数就为最大公因数
}

  但结合除数一定大于余数的知识和递归思想，我们却能进一步简化：

int gcd(int x, int y)
{
	return x % y == 0 ? y : gcd(y,x%y);
}

一个条件表达式，x%y==0吗，即余数等于0吗，如果等于，说明此时有我们想要的y值，如果不等于，继续调用gcd函数本身，依次下去，直到求出最大公因数。好好领悟，只有一行语句（当然也得保证第一次的形参是x>y），是不是简化了特别多？这就是递归奇妙的地方，当你找到某种规律时，递归很有可能就会派上用场。

二、hanoi（描述汉诺塔）

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

——《百度百科》

我们现在假设有这样一个情形：

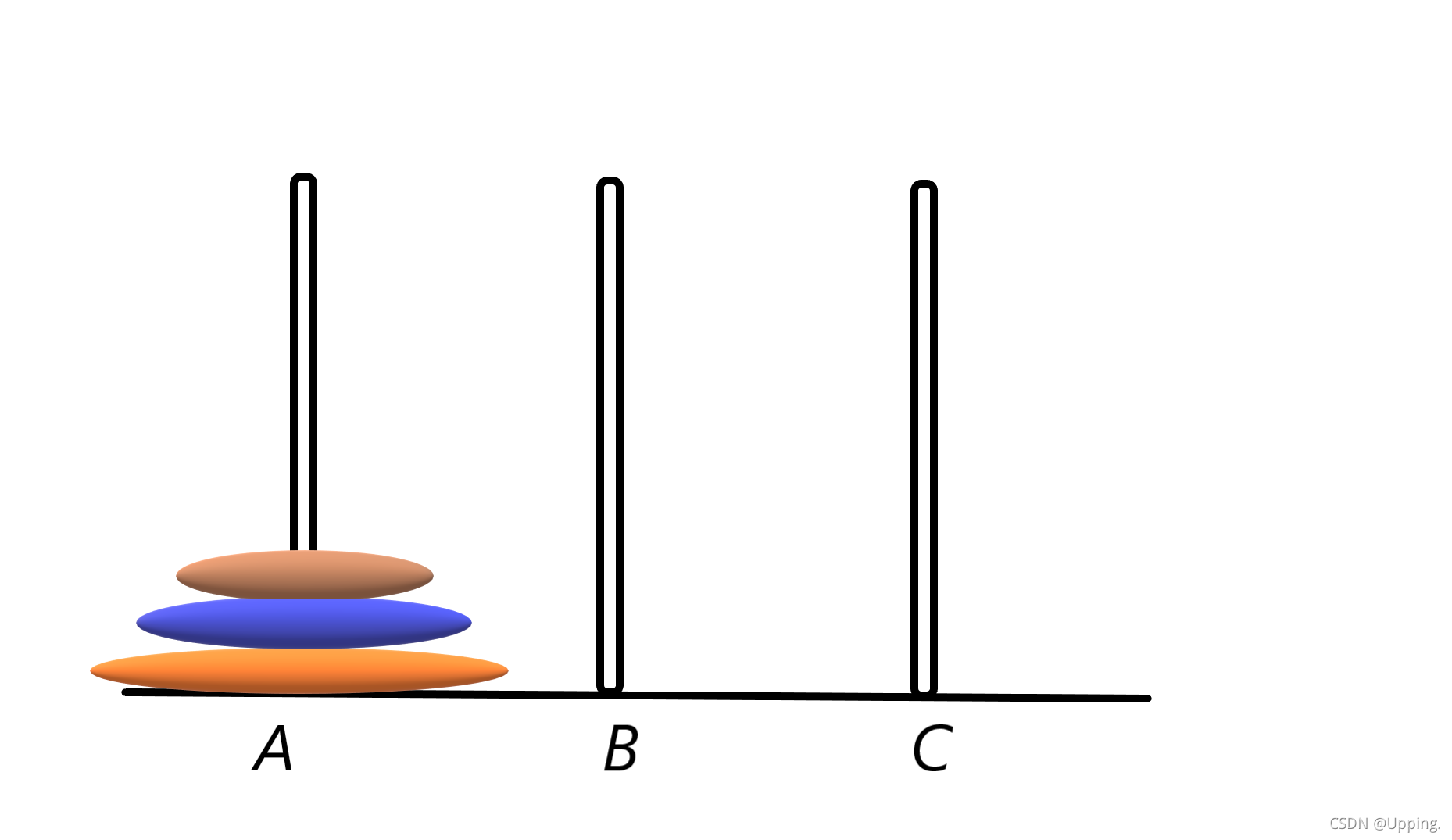
 要将A柱上的圆片按hanoi的规则移至C上，具体步骤该是怎样？

A->C        A->B        C->B        A->C        B->A        B->C        A->C

三层的汉诺塔还算简单，在脑海里模仿一遍便能得出，但是更多层呢？还有怎样让计算机跟我们想的一样并能输出步骤呢？

这就要用递归了，我们先自行模拟一下，试着找出规律。我们稍稍运用整体思想不难发现：要将整个汉诺塔移位，首先一个大步骤是将上两层移至B柱，接着将最底层移至最终层C柱，最后将上两层移至C柱。此时我们将移三层的7个步骤整理概括成了3个大步骤，我们可以再给这三个柱子命一个易懂的名字：起始柱（A），过渡柱（B），终点柱（C）。

概括一下：1、将（3-1）层从起始柱移动到过渡柱。

                  2、将最底层从起始柱移动到终点柱。

                  3、将（3-1）层从过渡柱移动到终点柱。

好了，任务其实已经完成了大半。接着我们怎么做？不妨继续顺着规律大胆的往下想下去。对于三层汉诺塔中的两层我们该怎样移？这里我们对“将（3-1）层从起始柱移动到过渡柱”分析，即两层汉诺塔从A到B,这时我们又可以利用递归了，对这两层来说，C柱才是过渡柱，B柱才是终点柱。

相信你也能对两层汉诺塔概括出类似的三个步骤。

接着一层呢？

我们结合gcd中递归的调用，我们会发现递归能将一个复杂的问题通过规律拆分成一个个最简单的式子。这里同样，我们可以将无数层的hanoi tower都拆成无数个1层hanoi来分析。

想想如何实现？

代码如下：

void hanoitower(int n, char A, char B, char C)//每个位置的形参含义分别是，一共有n层hanoi，需要从A 经过B 到C。
{
	if (n == 1)//当只有1层时，直接移动
		printf("%c-->%c\n", A, C);
	else
	{
		hanoitower(n - 1, A, C, B);//将n-1层从起始柱，经过过渡柱，到终点柱。
		printf("%c-->%c\n", A, C);//输出将最底层从起始柱移动到终点柱
		hanoitower(n - 1, B, A, C);//将n-1层从起始柱，经过过渡柱，到终点柱（观察参数细节）
	}
}

int main()
{
	char a = 'A';//定义塔序号
	char b = 'B';
	char c = 'C';
	int n;
	scanf("%d", &n);输入层数

	hanoitower(n, a, b, c);
	return 0;
}

当我们输入层数3时，看看输出结果：

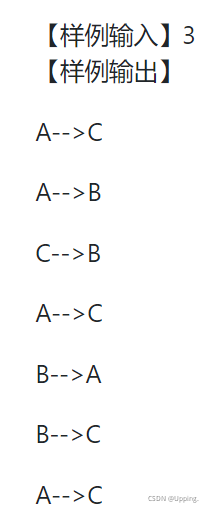
 与我们预想的一模一样。你学会了吗？

三、quicksort（快排）

（以下基于对《啊哈！算法》中相关篇章的理解）

关于排序，大家耳熟能详的大概是冒泡了，我们先想想冒泡是通过什么来实现的？双重for循环遍历，每发现相邻的两个数不符合排序要求就交换值，直到末尾。所以冒泡的核心就是交换。但每两个数之间都要判断一次，这在一些对时间复杂度度要求高的题目中，大概率就超时了。

这时结合了递归和二分思想的快排就站了出来，很好地解决了问题。那么快排是怎样的思路呢？

我们拿出一串乱序的数：3 1 2 5 4。需要用快排将它们从小到大排序。

1、我们先要设立一个基准数，用作参照，就默认第一个数字“3”吧。接着需要做的是将比基准数3小的数放在3的左边，比3大的放在其右边，这也符合排序的要求。

2、此时，我们不妨先将3尽量往这串数字的中间放，如何做到？我们抓住排序的本质“交换”，不过这次我们不单从一边了，我们两头都行动起来，向中间逼近。即从右往左找一个小于3的数，同时从左往右找一个大于3的数，我们要从小到大排，同时又设定了一个马上会处于一个相对中间位置的基准数。所以找出的两个数肯定是不符合顺序的，交换它们。我们将从两头向中间找的变量分别取名为哨兵i和哨兵j。即开始时哨兵i在开头（i=1）(位置在第一个)，哨兵j在末尾(j=5)（位置在第5个）。

3、这里因为基准数3设在最左边，每次就让最右边的哨兵j先移动，哨兵的操作时先判断，再移动。当前j=5，指向数字4，判断4是否小于基准数3？否，向左边移一位。接着轮到哨兵i移动了，指向数字3，是否<3？否，向右边移一位。又哨兵j，...，左移，指向数字2。哨兵i，...，右移，此时哨兵i也来到了数字2。两个哨兵在同一个位置碰面，共同指向数字2。这就是我们需要找的相对中间的位置。将基准数和2交换。

4、此时的数字串变成：2  1  3  5  4。下面需要用到一个二分的思想，即已已经归位的基准数3作为分界线，两边分别是“2  1”和“5  4”，想想接下来如何？我们继续对两边分别取基准数，并将其排在合适的位置。“2  1”里我们以2为基准数，2为哨兵i，1为哨兵j，不用说它们马上就碰面了，也就只有它们两个能交换，所以变成“1  2”,而“5  4”同理变成“4  5”，至此，所有数字都排好了序。

（emmmm，说着说着，发现这个例子举的数字太少了，不太好解释快排的操作...）

这里再以原书上的例子补充一下，帮助理解：

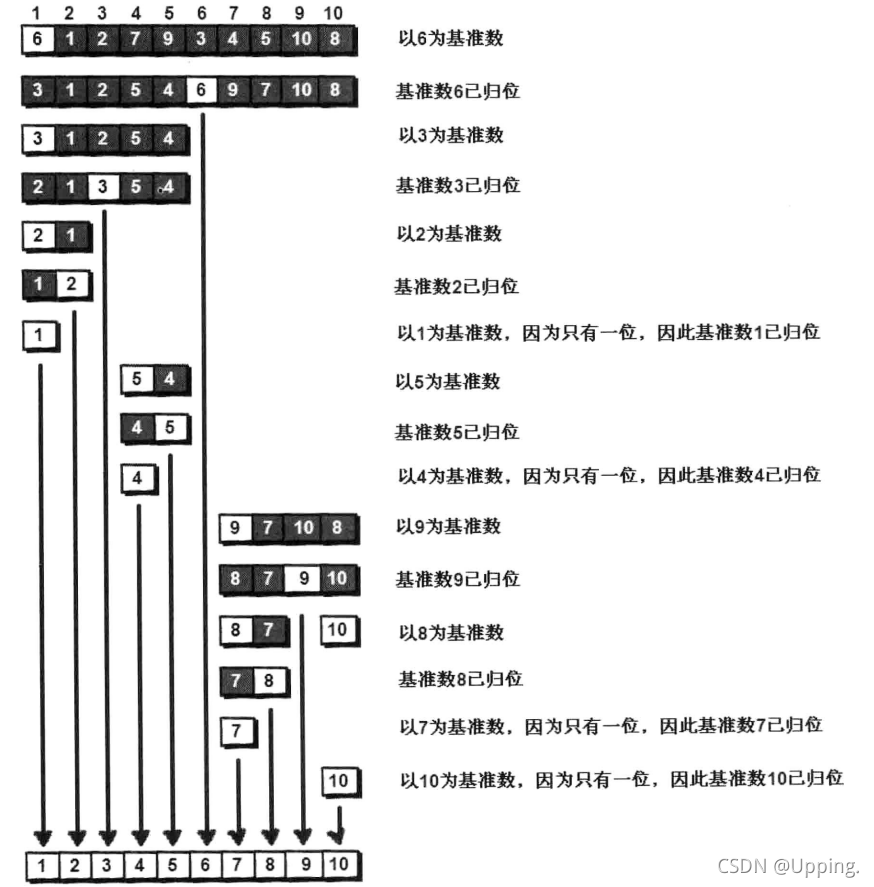
（来自《啊哈！算法》，侵权删）

那么代码如何实现呢？

#include<stdio.h>
#include<math.h>

int a[100001];//宏定义
int n;

void quicklysort(int left, int right)//两个哨兵的位置
{
	if (left > right)//想想递归的尽头是如何结束的
		return;
	int i, j, t, temp;
	i = left;//i哨兵在左
	j = right;//j哨兵在右
	temp = a[left];//设定基准数，为输入数字串的最左边的数

	while (i != j)//哨兵未相遇
	{
		while(a[j] >= temp && j > i)//哨兵j先动,先判断，再移动
			j--;
		while (a[i] <= temp && j > i)//哨兵i后动，也是先判断，再移动
			i++;

		if (i < j)//交换哨兵找到的不符合顺序的两值
		{
			t = a[i];
			a[i] = a[j];
			a[j] = t;
		}
	}

	a[left] = a[i];//运行到这两步说明哨兵已经碰面，找到了适中的位置，将基准数与其交换
	a[i] = temp;

	quicklysort(left, i - 1);//重点！递归调用，将基准数以左的数重新设立基准数和哨兵，进行一系列操作。
	quicklysort(i + 1, right);//基准数以右的数同理
	return;//都进行完了即排序完成！
}

int main()
{
	int i;
	scanf("%d", &n);//表示后面输入几个数

	for (i = 0; i < n; i++)
		scanf("%d", &a[i]);//将输入的数存入数组

	quicklysort(0, n - 1);//快排
	for (i = 0; i < n; i++)
		printf("%d ", a[i]); //将排好序的数输出。
    printf("\n");
	return 0;
}

 相比于冒泡排序，两者的核心虽都为交换，但快排是两边同时换，一次换两值，在大多数情况下都大大降低了时间复杂度，使程序运行不会超时。快排还运用了二分的思想，可能对于一部分同学来说，并不是很好理解。其实影响不大，我们这里重点关注的是其中的递归思想。

最后做个总结：递归是一种思想，可以说所有的运算都蕴含递归，递归无处不在。一个复杂的式子，当我们找到了其中的规律，又能用上递归思想的话，它将能被一层层拆分成无数条最简单基础的式子。并且代码实现会非常简洁。认识递归后，我们应该对它有更清晰的感知，并争取灵活运用它。

本周就分享到这里啦！

感谢你能看到这里，希望你有所收获，祝好！