看书标记【R语言数据分析项目精解：理论、方法、实战 4】

【R语言数据分析项目精解：理论、方法、实战】

Chapter 4 指标监控系统

4.1项目背景、目标方案

4.1.1项目背景

指标过多，人工跟踪工作量大，效率低，所以希望可以针对重要指标制定一套自动报警机制，把每天有异常的指标自动输出，达到有效降低人力成本的目的，进一步的，可以在这方面通过历史数据对未来进行预测。

4.1.2项目目标

针对重要指标建立预测模型，通过预测模型的95%预测上下限建立监控范围。这样就可以一举两得，预测模型可以对未来进行预估，另外95%上下限建立的范围可以用于监控，若当天数值超出当天预测值的监控范围，则报警。最后，通过可视化工具前端展示整个需求就可以了。

4.1.3项目方案

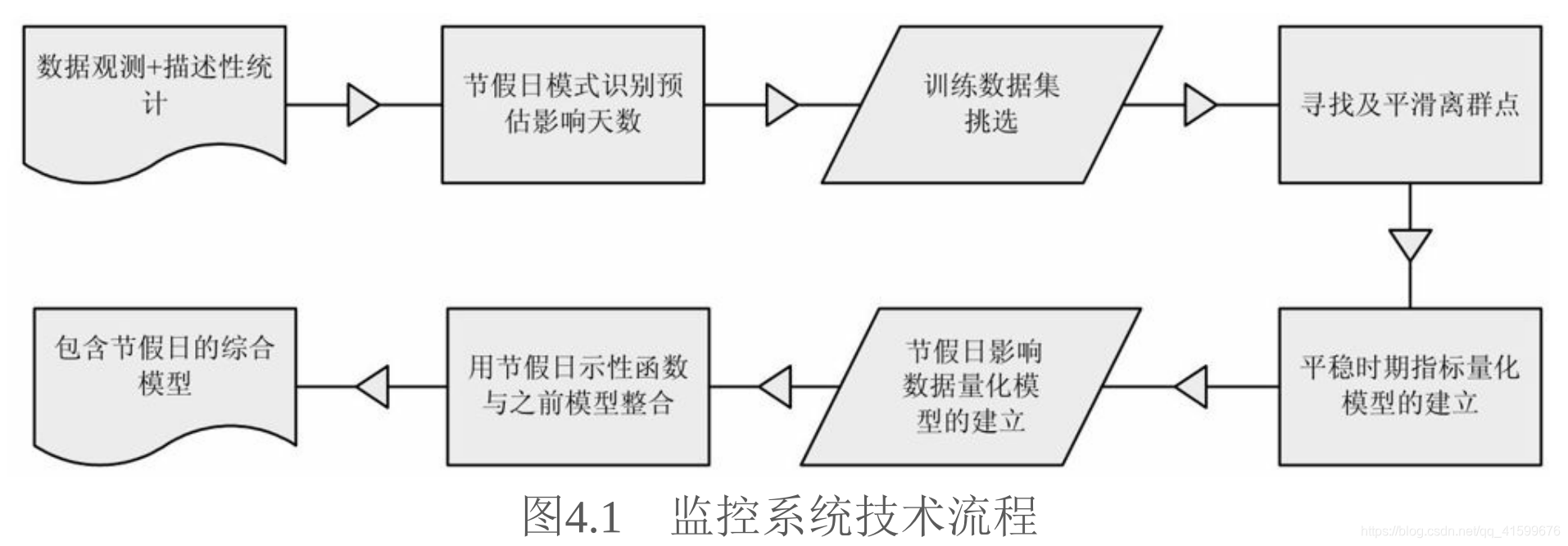
分成两种情况，节假日和非节假日。非节假日建立平稳时期指标量化模型，节假日建立影响数据量化模型，然后加一个示性函数，得到包含节假日的综合量化模型。

4.2项目技术理论简介

4.2.1时间序列基本统计量

时间序列均值和方差、自协方差函数和自相关函数

4.2.2数据观测与描述性统计

1.折线图：时间序列数据最直观的统计图形，能很好地反映整个趋势的走向和周期性，从而为下一步的分析提供指引性的先验知识。

2.平稳性：（严平稳）当序列所有的统计性质都不会随着时间的推移而发生变化；（宽平稳）当序列的统计性质只与时间间隔的变化而发生变化，以上两种都说明序列稳定。

3.检验方法：正态性检验（序列服从正态分布，一定平稳，所以也叫平稳性检验，此时H0：数据服从正态分布）；自相关图（自相关系数是否随着延迟期数的增加而迅速衰减到零，通常平稳序列具有6期以内的短期相关性，而后平稳）；单位根检验（单位根检验有单位根说明序列非平稳，非平稳序列在d阶差分后成平稳序列，称序列d阶单整。DF检验用于一阶自相关模型检验，ADF检验用于高阶自相关、高阶移动平均的模型，PP检验用于扰动项之间存在序列相关，KPSS检验用于序列是平稳或趋势平稳，优于DF检验）

4.非平稳序列平稳化：不通过平稳性检验的就变换序列使得变化后的序列通过平稳性检验。常用的变换方法有：差分变换、对数变换、Box-Cox变换。

4.2.3随机性

序列平稳后需对数据的随机性进行检验，若数据是随机的，那么对数据的近一步探讨建模将会是没有意义的。
Barlett定理、LB随机检验统计量

4.2.4周期性

除平稳性和随机性外，周期性也是时间序列的一个基本属性，除了折线图外，周期性还可以在谱分析的周期图中查看，高峰值可计算周期。

4.2.5节假日模式识别

针对带有周期的时间序列数据，提出周期相同天的配对t检验识别算法，找出带有周期的时间序列数据节假日影响模式的识别方法，具体步骤如下：
1.取原始数据》2.标注可疑的异常日期（主观标记）》3.周期相同天分组》4.周期相同天分组均值和》5.配对样本t检验

4.2.6建模数据集

1.挑选建模数据集

根据行业特征选取适合进行数据分析的时间范围内 的数据。

2.寻找离群点

噪声数据会对指标序列产生不利影响，一般来说，指标的不稳定性主要有：框架程序出错、导致记录不全；ETL调度工具运行不稳，导致用户行为记录不全甚至缺失；业务本身导致指标异常（举办活动等）；节假日因素。

先对“每周相同天定义”，同周期的第一天作为一个数据集，对每个集合使用检验方法（Grubbs检验、Dixon检验（小样本）、线箱图法（没有分布约束）和基于密度的局部异常因子法），挑出离群点。

3.平滑离群点

对于被剔除的离群点，通常会选择均值进行填补，具体的填补公式见P123详解。

4.2.7指标监控方法（不含节假日）

1.ARIMA模型

• AR模型：自回归模型又称为中心化的AR§模型，平稳过程为因果平稳（ AR模型的自相关系数是呈复指数衰减– 有拖尾性；AR模型的偏自相关系数有截尾性）
• MA模型：移动平均模型，MA模型总是平稳的，只有MA模型是依历史可逆的，该过程才具有预测意义（自相关系数q阶截尾；偏自相关系数q阶拖尾）
• ARMA模型：AR和MA的结合，所以性质与其相似
• 差分运算：p阶差分（p次只跨一个时刻）；k步差分（一次跨k个时刻）
• ARIMA模型：应用差分运算提取确定性信息后建模，所以ARIMA就是ARMA与差分运算的结合。

ARIMA模型模式识别
ACF法和PACF法判断p、q的值，或者AIC、BIC信息准则选取模型（autoarima中常用）

残差分析（真实值与模型预测值比较）
标准残差——时间图：零线上下无规则波动
标准残差的独立性检验：ACF图里滞后阶相关系数都在标准差范围内，则认为满足独立性检验。
残差随机性检验：广义方差检验和LB统计量检验（残差具有随机性则表明模型将规律部分全部提取）
正态性检验：Shapiro-Wilk检验和QQ图判断数据是否正态（残差符合正态分布，模型效果较好）

2.季节乘积ARIMA模型

季节乘积ARMA模型和季节乘积ARIMA模型（是否有差分运算的区别）

3.指数平滑

最近的数据对未来的影响更大，故应赋予较大的权重。指数平滑法本质上是对过去的数据进行加权和，距今越近，权重越高。

一次指数平滑：适用于序列无明显趋势，缺点是序列出现线性趋势时，一次指数平滑会出现严重滞后。
二次指数平滑：适用于序列存在线性趋势，缺点是序列出现周期性，则二次平滑预测序列偏差较大。
三次指数平滑：适用于序列存在线性及周期性趋势。累加和累乘，当季节变化在整个系列中大致恒定时，优选加法，而当季节变化与系列水平成比例变化时，优选乘法。

指数平滑对历史数据采取加权的方式比较符合实际情况，模型容易搭建，且具有自适应性，会根据数据变化自动变换。但是指数平滑模型对时间序列的转折点洞悉不足，适合短期预测。

4.质量控制图

用于监控产品零件生产品质
（1）适用条件：当监控指标变化较平稳且近似正态时，也可以用于互联网指标监控中。
（2）均值-极差控制图（hat_x—MR图）
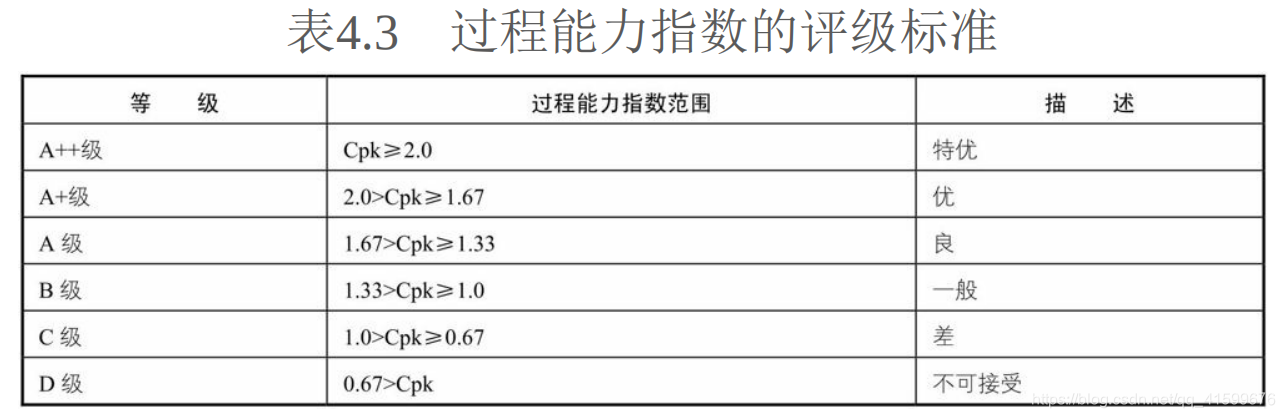
（3）过程能力指数：衡量了过程加工内在的一致性，表现的是加工过程固有的波动状态。

5.判断异常值的方法

季节乘积ARIMA模型和指数平滑模型由样本内拟合均方误差和样本外预测均方误差SSE的值选择，若拟合和预测选择的不一致，则可以，计算样本内两拟合均方误差的倒数得到两模型权重，随后以权重整合模型，得到预测值和置信限。

4.2.9R语言实例代码

1.Grubbs检验

######################################################################
#函数功能：Grubbs检验
#参数说明：x：要进行判断的数据
#####################################################################
library(outliers)
grubbs<-function(x){
  x<-round(x,4)
  grubbs_outliers<-c()
  grubbs_p.value<-c()
  grubbs_g.value<-c()
  grubbs_g<-c()
  grubbs_minormax<-c()
  grubbs_pvalue<-c()
  #设定初始值判断值
  grubbs_p<-0
  while(grubbs_p<0.05){
    grubbs_outliers<-c(grubbs_outliers,grubbs_minormax)
    grubbs_p.value<-c(grubbs_p.value,grubbs_pvalue)
    grubbs_g<-c(grubbs_g,grubbs_g.value)
    #去除最大、最小值然后再进行检验
    if(sum(x==grubbs_minormax)!=0)x<-x[-which(x==grubbs_minormax)]
    #若数据各值都相等则跳出
    if(sd(x)==0) break
    #进行grubbs检验
    grubbs_test<-grubbs.test(x,type=10,opposite=F,two.sided=F)
    grubbs_p<-grubbs_test$p.value
    grubbs_pvalue<-grubbs_test$p.value
    grubbs_g.value<-grubbs_test$statistic[1]
    grubbs_a<-strsplit(grubbs_test$alternative," ",fixed=T)
    grubbs_minormax<-as.numeric(unlist(grubbs_a)[3])
  }
  outliner_res<-data.frame(outliers=grubbs_outliers,gvalue=grubbs_g,pvalue=grubbs_p.value)
  return(outliner_res)
}

tt<-c(8.3,5.5,14,7.5,4.7,9,6.5,10.2,7.7,6.2)
grubbs(tt)

代码说明:grubbs. test是Grubbs检验实现函数，其调用格式为Grubbs. test (x，type=10，opposite=FALSE，two. sided=FALSE)。其中，参数x为检验数据向量；type=10表示检验一个异常值，type=11表示检验分别处于两个端点的异常值，type=20表示检验两个在同一侧的异常值；two. sided表示双边检验。上述代码通过Grubbs. test函数找出一个异常值，然后去除这个异常值再次检验，直到没有异常值为止，最后输出所有检验出来的异常值、G统计量和pvalue。

2.Dixon检验

######################################################################
#函数功能：Dixon检验
#参数说明：x：要进行判断的数据
#####################################################################
library(outliers)
dixon<-function(x){
    dixon_p.value<-c()
    dixon_q.value<-c()
    dixon_q<-c()
    dixon_pvalue<-c()
    dixon_outliers<-c()
    dixon_minormax<-c()
    dixon_p<-0
    while(dixon_p<0.05){
      dixon_outliers<-c(dixon_outliers,dixon_minormax)
      dixon_p.value<-c(dixon_p.value,dixon_pvalue)
      dixon_q<-c(dixon_q,dixon_q.value)
      if(sum(x==dixon_minormax)!=0)x<-x[-which(x==dixon_minormax)]
      if(sd(x)==0) break
      dixon_test<-dixon.test(x,type=0,opposite=F,two.sided=F)
      dixon_p<-dixon_test$p.value
      dixon_pvalue<-dixon_test$p.value
      dixon_q.value<-dixon_test$statistic[1]
      dixon_a<-strsplit(dixon_test$alternative," ",fixed=T)
      dixon_minormax<-as.numeric(unlist(dixon_a)[3])
    }
    outliner_res<-data.frame(outliers=dixon_outliers,qvalue=dixon_q,pvalue=dixon_p.value)
    return(outliner_res)
  }

tt<-c(8.3,5.5,14,7.5,4.7,9,6.5,10.2,7.7,6.2)
dixon(tt)

代码说明:函数思路和Grubbs检验的函数思路相似。dixon. test为Dixon检验的主要函数，其调用格式为dixon. test (x，type=10，
参数x为检验数据;
opposite=FALSE,two. sided=TRUE)。其中，
type=10表示检验数据集为8～10个的数据，type=21表示检验数据集为11～13个的数据，type=22表示检验数据集为14个或14个以上的数据;two. sided表示双边检验。通过自定义的Dixon检验函数，没有发现异常值。

3.LOF检验

########################################################################
#函数功能：lof检验
#参数说明：x：要进行判断的数据
########################################################################
library(DMwR)
library(outliers)

loffun<-function(klb,kup,indexnum){
    lof_value<-c()
    indexdata<-indexnum
    indexname<-"indexdata"
    index_lof<-data.frame(indexdata=indexdata)

    for (k in klb:kup){
    lof_score<-paste("lof_score",k,"<-lofactor(",indexname,",",k,")",sep="")
    add_lof<-paste("index_lof$lof_score",k,"<-lof_score",k,sep="")
    eval(parse(text=lof_score))
    eval(parse(text=add_lof))
    cr_lofresult<-paste("lof_value<-apply(cbind(lof_value,lof_score",k,"),1,max)",sep="")
    eval(parse(text=cr_lofresult))
    }
   
    index_lof$lofvalue<-round(lof_value,2)    
    index_lof$num<-1
    lof_thres<-grubbs(index_lof$lofvalue)
    index_lof$lofflag<-c(rep(0,nrow(index_lof)))
    index_lof[index_lof$lofvalue%in%lof_thres$outliers,]$lofflag<-1
    lof_result<-subset(index_lof,lofflag==1)
    lof_result[order(-lof_result$lofvalue),]
    lof_data<-lof_result[,c("indexdata","lofvalue")]
    lof_data[order(-lof_data$lofvalue),]

    return(lof_data) 
}
klb<-10
kup<-14

#生成测试数据
indexdata<-c(2,1,2,3,2,3,4,5,6,5,4,3,22,1,2,3,4,0,2,33)
loffun(klb,klb,indexdata)

代码说明: lofactor函数用于LOF离群点的判断，其中k为每个族中最少包含的元素个数。通过循环函数，对不同k的可能取值依次计算LOF值，然后取最大的一个作为该数值的LOF值;接着用前面的Grubbs函数确定LOF阈值（找出离群点），最终LOF值离群点对应的数值即为样本离群点。假定k取10～14，通过循环检验，最终找出了10个离群点。

4.指数平滑

HoltWinters(co2) #三次指数平滑

5.均值-极差图

#####################################################################
#函数功能：极差均值控制图
#参数说明：x：要进行判断的数据
#####################################################################
xmr<-function(index){
  opar <- par(no.readonly=TRUE)
  par(mfrow=c(2,1))
  color<-c("green","red")
  title1<-paste("cr_xmr_单值",sep="")
  title2<-paste("cr_xmr_移动极差",sep="")

 #计算极差均值数据
  R<-abs(diff(index))
  Rbar<-mean(R)
  xbar<-mean(index)
  xucl<-xbar+2.66*Rbar
  xlcl<-xbar-2.66*Rbar
  Rucl<-3.267*Rbar
  Rlcl<-0

  #作图
  plot(index,ylim=c(xlcl-0.2*xlcl,xucl+0.2*xucl),type='o',pch=19,main=title1,col=color[1])
  abline(h=xucl,col=color[2])
  abline(h=xlcl,col=color[2])

  plot(R,ylim=c(Rlcl-0.2*Rlcl,Rucl+0.2*Rucl),type='o',pch=19,main=title2,col=color[1])
  abline(h=Rucl,col=color[2])
  abline(h=Rlcl,col=color[2])  
  par(opar)

  interval<-list(ucl=xucl,lcl=xlcl)
  return(interval)
}

#生成指标
indexdata<-c(0.1071,0.1097,0.1069,0.116,0.0893,0.0877,0.1181,0.1107,0.1122)
xmr(indexdata)

4.3项目实践

4.3.1数据概览

文中用到的是订单支付转化率，CR是一个相对平稳的指标，结合了订单和流量这两个核心指标，也是KPI重要的核心指标。

1.折线图

#数据获取
setwd("C:\\Users\\用户路径")
crtot<-read.csv("2011~2016.10总体数据.csv",header=TRUE)
crtot$orderdate<-as.Date(crtot$orderdate)
indexdata<-crtot$indexdata
x.text<-crtot$orderdate

#总体折线图
plot(indexdata,type="l",xaxt="n",xlab="日期",ylab="数值")
abline(h=mean(indexdata))
axis(1,at=1:length(indexdata),labels=x.text,tick=FALSE)

#每年折线图
crtot$year<-as.numeric(format(crtot$orderdate,"%Y"))

flt_11<-subset(crtot,year==2011)
flt_12<-subset(crtot,year==2012)
flt_13<-subset(crtot,year==2013)
flt_14<-subset(crtot,year==2014)
flt_15<-subset(crtot,year==2015)
flt_16<-subset(crtot,year==2016)

id=c("2011年","2012年","2013年","2014年","2015年","2016年")
col=c("black","red","orange","purple","yellow","blue")

plot(flt_11$indexdata,type='l',ylim=c(0,0.2),col=col[1],main="各年数据")
legend("topleft",legend=id,horiz=T,pch=15,col=col,cex=0.8,bty="n")
lines(flt_12$indexdata,col=col[2])
lines(flt_13$indexdata,col=col[3])
lines(flt_14$indexdata,col=col[4])
lines(flt_15$indexdata,col=col[5])
lines(flt_16$indexdata,col=col[6])

每年同期的折线图基本平稳

2.平稳性检验

library(TSA)
adfresult<-adf.test(indexdata,alt="stationary") #adf检验
adfresult

3.随机性检验

Box.test(indexdata, type="Ljung-Box",lag=6)
Box.test(indexdata, type="Ljung-Box",lag=12)

4.周期性检验
根据行业情况判断周期，普遍为7天，文中有用谱分析中的周期图来验证7天的假设是否正确。每年的指标数据大致相同；节假日对数据整体影响较大，所以先提出固定节假日的数据。

flt_pfx<-subset(flt_16,orderdate>='2016-06-01' & orderdate<='2016-09-09') #选取样本数据
pr<-periodogram(flt_pfx$indexdata)  #画出谱分析中的周期图
score1<-pr$freq[which(pr$spec==max(pr$spec))]  #计算最高点对应的周期
f<-1/score1 ;f  #周期

由最高尖峰的频率来计算，1/0.1388=7.2046天

4.3.2节假日模式识别

1.节假日模式分类

根据各指标节前、节中、节后的不同变化趋势，对节假日期间的指标进行大致分类。

2.转化率指标节假日模式识别

文中用的是国庆节相关数据，首先要对指标数据打上假日标识，大致确定节前、节中、节后的时间段。

library(plyr)
holidayflag<-read.csv("holiday.csv",header=TRUE,stringsAsFactors=FALSE)   #读取节假日标识数据
holidayflag$orderdate<-as.Date(holidayflag$orderdate)
flt<-read.csv("2011~2016.10总体数据.csv",header=TRUE)  #读取指标数据
flt$orderdate<-as.Date(flt$orderdate)
flt<-join(flt,holidayflag) #将节假日标识打在指标数据上
flt$year<-as.numeric(format(flt$orderdate,"%Y"))
#每年数据分别存储
flt_11<-subset(flt,year==2011)
flt_12<-subset(flt,year==2012)
flt_13<-subset(flt,year==2013)
flt_14<-subset(flt,year==2014)
flt_15<-subset(flt,year==2015)
flt_16<-subset(flt,year==2016)

#国庆前后明细数据图

id=c("2011年","2012年","2013年","2014年","2015年","2016年")
col=c("black","red","orange","purple","yellow","blue")

xtext<-paste(format(flt_11_2$orderdate,"%m"),format(flt_11_2$orderdate,"%d"),sep='-')
plot(flt_11_2$indexdata,type='l',xaxt='n',col=col[1],ylim=c(0,0.2),main="国庆前后明细数据")
axis(1,at=1:61,labels=xtext,tick=FALSE)
legend("topleft",legend=id,horiz=T,pch=15,col=col,cex=0.8,bty="n")
lines(flt_12_2$indexdata,col=col[2])
lines(flt_13_2$indexdata,col=col[3])
lines(flt_14_2$indexdata,col=col[4])
lines(flt_15_2$indexdata,col=col[5])
lines(flt_16_2$indexdata,col=col[6])

然后周期相同天组成各自对应的样本集，计算出均值与之匹配，实现样本的配对

##周期相同天数据整理
flt_11$number<-c(rep(1:7,nrow(flt_11)%/%7),c(1:7)[1:(nrow(flt_11)%%7)])
flt_12$number<-c(rep(1:7,nrow(flt_12)%/%7),c(1:7)[1:(nrow(flt_12)%%7)])
flt_13$number<-c(rep(1:7,nrow(flt_13)%/%7),c(1:7)[1:(nrow(flt_13)%%7)])
flt_14$number<-c(rep(1:7,nrow(flt_14)%/%7),c(1:7)[1:(nrow(flt_14)%%7)])
flt_15$number<-c(rep(1:7,nrow(flt_15)%/%7),c(1:7)[1:(nrow(flt_15)%%7)])
flt_16$number<-c(rep(1:7,nrow(flt_16)%/%7),c(1:7)[0:(nrow(flt_16)%%7)])

#----------离群点判断----------------
library(outliers)
library(DMwR)
##Grubbs'Test
Grubbs<-function(initial,cycle){
  grubbs<-function(x){
    x<-round(x,6)
    grubbs_outliers<-c()
    grubbs_minormax<-c()
    grubbs_p<-0
    while(grubbs_p<0.05){
      grubbs_outliers<-c(grubbs_outliers,grubbs_minormax)
      if(sum(x==grubbs_minormax)!=0)x<-x[-which(x==grubbs_minormax)]
      if(sd(x)==0) break
      grubbs_test<-grubbs.test(x,type=10,opposite=F,two.sided=F)
      grubbs_p<-grubbs_test$p.value
      grubbs_a<-strsplit(grubbs_test$alternative," ",fixed=T)
      grubbs_minormax<-as.numeric(unlist(grubbs_a)[3])
    }
    return(grubbs_outliers)
  }
  Grubbs.outliers<-tapply(initial$indexdata,initial$number,grubbs)
  initial$Grubbs.test<-rep(0,nrow(initial))
  for(i in 1:cycle){
    initial$Grubbs.test[which(initial$indexdata%in%Grubbs.outliers[[i]]&initial$number==i)]<-1
  }
  return(initial)
}

##Boxplot
Boxplot<-function(initial,cycle){
  Boxplot.outliers<-tapply(initial$indexdata,initial$number,function(x) boxplot.stats(x)$out)
  initial$Boxplot.test<-rep(0,nrow(initial))
  for(i in 1:cycle){
    initial$Boxplot.test[which(initial$indexdata%in%Boxplot.outliers[[i]]&initial$number==i)]<-1
  }
  return(initial)
}

##Lofactor
Lof<-function(initial){
  initial$Lof.test<-rep(0,nrow(initial))
  Lof.scores<-lofactor(initial$indexdata,k=floor(nrow(initial)/10))
  Lof.outliers<-initial$indexdata[which(Lof.scores>1.75)]
  initial$Lof.test[which(Lof.scores>1.75)]<-1
  return(initial)
}

holvalue<-function(tbdata){
  res_after4<-subset(tbdata,orderdate>=paste(unique(tbdata$year),"-06-01",sep='') & orderdate<=paste(unique(tbdata$year),"-09-16",sep=''))

  grubbs<-Grubbs(res_after4,7)
  boxplot<-Boxplot(res_after4,7)
  lof<-Lof(res_after4)

  res_after4$Grubbs.test<-grubbs$Grubbs.test
  res_after4$Boxplot.test<-boxplot$Boxplot.test
  res_after4$Lof.test<-lof$Lof.test
  res_after4$abnflag<-res_after4$Grubbs.test+res_after4$Boxplot.test+res_after4$Lof.test

  tb_adj<-subset(res_after4,abnflag<2)
  tb_adjmean<-aggregate(tb_adj$indexdata,by=list(tb_adj$number),mean)
  names(tb_adjmean)[1]<-"number"

  tb_hol<-subset(tbdata,complete.cases(tbdata$flag))
  tb_rb<-merge(tb_hol,tb_adjmean,all.tb_hol=TRUE)
  return(tb_rb)
}

############相同周期点配对数据输出调整格式#############
flt_11hol_adj<-flt_11hol[order(flt_11hol$flag),]
flt_12hol_adj<-flt_12hol[order(flt_12hol$flag),]
flt_13hol_adj<-flt_13hol[order(flt_13hol$flag),]
flt_14hol_adj<-flt_14hol[order(flt_14hol$flag),]
flt_15hol_adj<-flt_15hol[order(flt_15hol$flag),]
flt_16hol_adj<-flt_16hol[order(flt_16hol$flag),]

flt_11hol_adj$date<-paste(format(flt_11hol_adj$orderdate,'%m'),'-',format(flt_11hol_adj$orderdate,'%d'),sep='')
flt_12hol_adj$date<-paste(format(flt_12hol_adj$orderdate,'%m'),'-',format(flt_12hol_adj$orderdate,'%d'),sep='')
flt_13hol_adj$date<-paste(format(flt_13hol_adj$orderdate,'%m'),'-',format(flt_13hol_adj$orderdate,'%d'),sep='')
flt_14hol_adj$date<-paste(format(flt_14hol_adj$orderdate,'%m'),'-',format(flt_14hol_adj$orderdate,'%d'),sep='')
flt_15hol_adj$date<-paste(format(flt_15hol_adj$orderdate,'%m'),'-',format(flt_15hol_adj$orderdate,'%d'),sep='')
flt_16hol_adj$date<-paste(format(flt_16hol_adj$orderdate,'%m'),'-',format(flt_16hol_adj$orderdate,'%d'),sep='')

names(flt_11hol_adj)[c(3,6)]<-c("2011index","2011avg")
names(flt_12hol_adj)[c(3,6)]<-c("2012index","2012avg")
names(flt_13hol_adj)[c(3,6)]<-c("2013index","2013avg")
names(flt_14hol_adj)[c(3,6)]<-c("2014index","2014avg")
names(flt_15hol_adj)[c(3,6)]<-c("2015index","2015avg")
names(flt_16hol_adj)[c(3,6)]<-c("2016index","2016avg")
flt_11hol_adj<-flt_11hol_adj[,c("flag","date","2011index","2011avg")]
flt_12hol_adj<-flt_12hol_adj[,c("flag","date","2012index","2012avg")]
flt_13hol_adj<-flt_13hol_adj[,c("flag","date","2013index","2013avg")]
flt_14hol_adj<-flt_14hol_adj[,c("flag","date","2014index","2014avg")]
flt_15hol_adj<-flt_15hol_adj[,c("flag","date","2015index","2015avg")]
flt_16hol_adj<-flt_16hol_adj[,c("flag","date","2016index","2016avg")]

flt_tot_adj<-merge(flt_11hol_adj,flt_12hol_adj)
flt_tot_adj<-merge(flt_tot_adj,flt_13hol_adj)
flt_tot_adj<-merge(flt_tot_adj,flt_14hol_adj)
flt_tot_adj<-merge(flt_tot_adj,flt_15hol_adj)
flt_tot_adj<-merge(flt_tot_adj,flt_16hol_adj)
write.csv(flt_tot_adj,"相同周期点配对数据.csv")  #结果输出到本地

先用两种及以上方法剔除对均值会有影响的离群点，然后计算均值后的配对样本数据调整格式并输出。

#------3）配对T检验
flt_tot<-rbind(flt_11hol,flt_12hol,flt_13hol,flt_14hol,flt_15hol,flt_16hol)
#配对T检验函数
tvalue<-function(id,flt_tot){
  aa<-subset(flt_tot,flag==id)$indexdata
  bb<-subset(flt_tot,flag==id)$x
  t_value<-t.test(aa,bb,paired=TRUE)$p.value
  return(t_value)
}
#针对每个日期，进行配对T检验
ttest_pvalue<-unlist(lapply(sort(unique(flt_tot$flag)),tvalue,flt_tot))
result_pvalue<-data.frame(flag=sort(unique(flt_12hol$flag)),pvalue=ttest_pvalue)

#计算均值
indexdata_avg<-aggregate(flt_tot$indexdata,by=list(flt_tot$flag),mean)
x_avg<-aggregate(flt_tot$x,by=list(flt_tot$flag),mean)
names(x_avg)[2]<-"xavg"
x_avg_df<-merge(indexdata_avg,x_avg,all.indexdata_avg=TRUE)
names(x_avg_df)[1]<-'flag'

ttest_result<-merge(x_avg_df,result_pvalue)
ttest_result$x_cf<-rep("higher",nrow(ttest_result))
ttest_result[which(ttest_result$x<=ttest_result$xavg),]$x_cf<-"lower"
ttest_result$pvalueflag<-rep("F",nrow(ttest_result))
ttest_result[which(ttest_result$pvalue<0.01),]$pvalueflag<-"T"

4.3.3模型数据集的建立

1.挑选数据集

cr<-read.csv("建模数据1031-带异常值.csv",header=TRUE)  #读取数据
cr$orderdate<-as.Date(cr$orderdate)
cr<-subset(cr,cr$orderdate<='2016-09-11')
cycle<-7  #设置周期
cr$number<-rep(1:cycle,len=nrow(cr))
xtext<-paste(format(cr$orderdate,"%m"),format(cr$orderdate,"%d"),sep='-')  #画出折线图
plot(cr$indexdata,type='l',xaxt='n')
axis(1,at=1:length(cr$orderdate),labels=xtext,tick=FALSE)

2.寻找离群点

#--Grubbs检验
Grubbs.outliers<-tapply(cr$indexdata,cr$number,grubbs)
cr$grubbsflag<-c(rep(0,nrow(cr)))

for(i in 1:cycle){
    if(nrow(Grubbs.outliers[[i]])>0){
        grubbs_df<-subset(Grubbs.outliers[[i]],pvalue<=0.1)
        grubbs_outliers<-grubbs_df$outliers
        cr$grubbsflag[which(cr$indexdata%in%grubbs_outliers&cr$number==i)]<-1
    }
}

head(cr)


#--Dixon检验
Dixon.outliers<-tapply(cr$indexdata,cr$number,dixon)
cr$dixonflag<-c(rep(0,nrow(cr)))
for(i in 1:cycle){
    if(nrow(Dixon.outliers[[i]])>0){
        dixon_df<-subset(Dixon.outliers[[i]],pvalue<=0.1)
        dixon_outliers<-dixon_df$outliers
        cr$dixonflag[which(cr$indexdata%in%dixon_outliers&cr$number==i)]<-1
    }
}

head(cr)

#--线箱图
Boxplot.outliers<-tapply(cr$indexdata,cr$number,function(x) boxplot.stats(x)$out)
cr$boxplotflag<-rep(0,nrow(cr))
for(i in 1:cycle){
    cr$boxplotflag[which(cr$indexdata%in%Boxplot.outliers[[i]]&cr$number==i)]<-1
}

head(cr)

#--LOF局部离群点
klb<-10
kup<-14
crlof<-loffun(klb,kup,cr$indexdata)
cr$lofflag<-c(rep(0,nrow(cr)))
cr$lofflag[which(cr$indexdata%in%crlof$indexdata)]<-1

head(cr)

#--整合四种方法
cr$outlierflag<-cr$grubbsflag+cr$dixonflag+cr$boxplotflag+cr$lofflag
#查看总体结果
head(cr[order(-cr$outlierflag),],10)

至少有两种方法判定为离群点（“1”）的数据可以是真正的离群点。
3.离群点平滑：普遍采用均值填补

4.3.4指标监控（非节假日）

1.数据概览

建模

crdf<-read.csv("建模数据1031-带异常值 平滑后 adj.csv",header=TRUE)  #获取数据
crdf$orderdate<-as.Date(crdf$orderdate)

#9月11日之前用来建模，9月12日~9月18日的用来检验
cr_df<-subset(crdf,orderdate<='2016-09-11')
cr_tot<-cr_df$indexdata

plot(cr_tot,type='o')  #画折线图
abline(h=mean(cr_tot))

#计算自相关图和偏自相关
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
acf(cr_tot,lag.max=60)
pacf(cr_tot,lag.max=60) 
par(opar) 

#随机性检验
Box.test(cr_tot, type="Ljung-Box",lag=6)
Box.test(cr_tot, type="Ljung-Box",lag=12)

#平稳化检验
library(TSA)
adfresult<-adf.test(cr_tot,alt="stationary") #adf检验

原始序列具有7天的周期；Ljung-Box检验，p<0.05拒绝H0:序列随机的假设，有相关性信息；ADF检验，p<0.05拒绝H0:序列有单位根的假设，序列平稳。

2.乘积季节模型的建立

#选择ARIMA(0,1,2)×(2,0,1)7.
library(forecast)
arimatt_opt<-arima(cr_tot,order=c(0,1,2),seasonal=list(order=c(2,0,1),period=7),method='ML')
arimatt_opt
#残差分析
res<-arimatt_opt$res  #计算残差
#残差-时间图
plot(rstandard(arimatt_opt),ylab='Standardized Residuals',main='标准残差-时间')
abline(h=0)
acf(res,main="ACF of residuals",lag.max=60)   #残差独立性检验

#随机性检验
#----广义方差检验
library(portes)
plot(gvtest(arimatt_opt,1:60)[,4],main="广义方差检验",ylab='p-value   ',xlab="lag",pch=16,ylim=c(0,1))
abline(h=0.05,lty=2)
#----LB检验
Box.test(res, type="Ljung-Box",lag=6)

#正态性检验
qqnorm(res)
qqline(res)
sol<-shapiro.test(res)   #原假设：数据服从正太分布
sol


#---模型拟合与预测
prop.fore = predict(arimatt_opt, n.ahead =7)
#95%预测上线限
u<- prop.fore$pred + 1.96* prop.fore$se 
l<-prop.fore$pred-1.96*prop.fore$se
cr_ts<-ts(cr_tot,frequency=1)
ts.plot(cr_ts, prop.fore$pred, col=c("black","blue")) 
lines(u, col="red", lty="dashed")
lines(l, col="red", lty="dashed") 
#样本内拟合
fit<-cr_tot-res
lines(fit,col="chocolate") 

#样本外预测
cryz<-subset(crdf,orderdate>='2016-09-12' & orderdate<='2016-09-18')
realvalue<-cryz$indexdata
outlinepre_ar<-data.frame(pre=prop.fore$pred,realvalue=realvalue)

3.三次指数平滑

#模型拟合
cr_ts <- ts(cr_tot, frequency=7,start=c(1987,1))
plot.ts(cr_ts)
cr_ht <- HoltWinters(cr_ts)
plot(cr_ht)

#残差分析
e<-cr_ht$x-cr_ht$fitted[,1]   #计算残差
plot(e,ylab='Standardized Residuals',main='标准残差-时间')  #残差-时间图
abline(h=0)
acf(e,main="ACF of residuals",lag.max=60)   #独立性检验
Box.test(e, type="Ljung-Box",lag=6)   #随机性检验
Box.test(e, type="Ljung-Box",lag=12)

#正态性检验 #QQ图
qqnorm(e)
qqline(e)
sol<-shapiro.test(e)   #原假设：数据服从正太分布

#（3）拟合与预测
library("forecast")
fitvalue<-fitted(cr_ht)[,1]  #样本内预测
plot(cr_ts)
lines(fitvalue,col='chocolate')

cr_ht_fore <- forecast.HoltWinters(cr_ht, h=7)  #样本外预测
plot.forecast(cr_ht_fore)

#95%样本外预测上下限
l<-cr_ht_fore[5]$lower[,2]
u<-cr_ht_fore[6]$upper[,2]

#样本外预测均方误
outlinepre_hw<-data.frame(realvalue=realvalue,prevalue=cr_ht_fore[[4]])

#（4）整合乘积季节模型和Holt-Winters模型
#乘积季节模型样本内拟合均方误
inline_mse_ar<-mean(abs(arimatt_opt$res)^2)
#Holt-Winter样本内拟合均方误
inline_mse_hw<-mean(e^2)
#乘积季节模型样本外拟合均方误
outline_mse_ar<-mean((outlinepre_ar$pre-outlinepre_ar$realvalue)^2)
#Holt-Winter样本外拟合均方误
outline_mse_hw<-mean((outlinepre_hw$realvalue-outlinepre_hw$prevalue)^2)
modelcf<-matrix(rep(0,4),nrow=2)
rownames(modelcf)<-c("样本内拟合均方误","样本外预测均方误")
colnames(modelcf)<-c("季节乘积模型","Holt-Winters")
modelcf[1,]<-c(inline_mse_ar,inline_mse_hw)
modelcf[2,]<-c(outline_mse_ar,outline_mse_hw)

4.质量监控图

#（1）对每周相同天集合做正态性检验
crdf<-read.csv("建模数据1031-带异常值 平滑后 adj.csv",header=TRUE)
crdf$orderdate<-as.Date(crdf$orderdate)

cycle<-7
cr_df<-subset(crdf,orderdate<='2016-09-11')
cr_df$number<-rep(1:cycle,len=nrow(cr_df))

#正态性检验函数
normtest<-tapply(cr_df$indexdata,list(cr_df$number),shapiro.test)

weekday<-c("周一","周二","周三","周四","周五","周六","周日")
normpvalue<-c()
for (i in 1:7){
  normpvalue<-c(normpvalue,normtest[[i]]$p.value)
}

normtest<-data.frame(weekday=weekday,pvalue=normpvalue)
normtest

#（2）制作X-MR分析用控制图
##################################################################
#函数功能：极差均值控制图
#参数说明：df 数据框
#i：整数值
##################################################################
xmr<-function(df,i){
  opar <- par(no.readonly=TRUE)
  par(mfrow=c(2,1))
  color<-c("green","red")
  index<-subset(df,number==i)$indexdata
  title1<-paste("cr_xmr_单值：第",i,"组",sep="")
  title2<-paste("cr_xmr_移动极差：第",i,"组",sep="")

  R<-abs(diff(index))
  Rbar<-mean(R)
  xbar<-mean(index)
  xucl<-xbar+2.66*Rbar
  xlcl<-xbar-2.66*Rbar
  Rucl<-3.267*Rbar
  Rlcl<-0

  plot(index,ylim=c(xlcl-0.2*xlcl,xucl+0.2*xucl),type='o',pch=19,main=title1,col=color[1])
  abline(h=xucl,col=color[2])
  abline(h=xlcl,col=color[2])

  plot(R,ylim=c(Rlcl-0.2*Rlcl,Rucl+0.2*Rucl),type='o',pch=19,main=title2,col=color[1])
  abline(h=Rucl,col=color[2])
  abline(h=Rlcl,col=color[2])
  par(opar) 

  interval<-list(ucl=xucl,lcl=xlcl)
  return(interval)
}

xmr_1<-xmr(cr_df,1)
#均值和移动极差都在范围内，对有超出范围的部分，需要对该组数据进行分析和修正
xmr_3<-xmr(cr_df,3)

index<-subset(cr_df,number==3)$indexdata
abs(diff(index))
##所以需要去除第12个值后再进行计算

index<-subset(cr_df,number==3)$indexdata
abs(diff(index))
i<-3
index<-index[-length(index)]
title1<-paste("cr_xmr_单值：第",i,"组",sep="")
title2<-paste("cr_xmr_移动极差：第",i,"组",sep="")

R<-abs(diff(index))
Rbar<-mean(R)
xbar<-mean(index)
xucl_3_adj<-xbar+2.66*Rbar
xlcl_3_adj<-xbar-2.66*Rbar
Rucl<-3.267*Rbar
Rlcl<-0
color<-c("green","red")
plot(index,ylim=c(xlcl_3_adj-0.2*xlcl_3_adj,xucl_3_adj+0.2*xucl_3_adj),type='o',pch=19,main=title1,col=color[1])
abline(h=xucl_3_adj,col=color[2])
abline(h=xlcl_3_adj,col=color[2])

plot(R,ylim=c(Rlcl-0.2*Rlcl,Rucl+0.2*Rucl),type='o',pch=19,main=title2,col=color[1])
abline(h=Rucl,col=color[2])
abline(h=Rlcl,col=color[2])
##由质量监控图知，第三组均值和移动极差均在范围内

#（3）上下限确定
xmr_1<-xmr(cr_df,1)
xmr_2<-xmr(cr_df,2)
xmr_4<-xmr(cr_df,4)
xmr_5<-xmr(cr_df,5)
xmr_6<-xmr(cr_df,6)
xmr_7<-xmr(cr_df,7)

weekday<-c("周一","周二","周三","周四","周五","周六","周日")
ucl_interval<-c(xmr_1$ucl,xmr_2$ucl,xucl_3_adj,xmr_4$ucl,xmr_5$ucl,xmr_6$ucl,xmr_7$ucl)
lcl_interval<-c(xmr_1$lcl,xmr_2$lcl,xlcl_3_adj,xmr_4$lcl,xmr_5$lcl,xmr_6$lcl,xmr_7$lcl)

xmr_interval<-data.frame(weekday=weekday,ucl=round(ucl_interval,4),lcl=round(lcl_interval,4))
##给出转化率指标的最小值后，可以计算得到过程能力指数，将之与登记表对比可得过程稳定。
#### 4.3.5 节假日指标监控
##### 1.预测节假日数据
```r
library(TSA)
library(portes)
library(forecast)
crdf<-read.csv("建模数据1031-带异常值 平滑后 adj.csv",header=TRUE)
crdf$orderdate<-as.Date(crdf$orderdate)
cr_df<-subset(crdf,orderdate<='2016-09-18')
cr_tot<-cr_df$indexdata

arimatt_opt<-arima(cr_tot,order=c(0,1,2),seasonal=list(order=c(2,0,1),period=7),method='ML')
prop.fore <- predict(arimatt_opt, n.ahead =25)
#95%预测上线限
ucl_ar<- prop.fore$pred + 1.96* prop.fore$se 
lcl_ar<-prop.fore$pred-1.96*prop.fore$se
cr_hol<-subset(crdf,orderdate>='2016-09-19' & orderdate<='2016-10-13')
crhol<-data.frame(indexdata=cr_hol$indexdata,pred=prop.fore$pred)
crhol$diff<-crhol$indexdata-crhol$pred
crhol

2.差值建模

cr_tot_diff<-crhol$diff
plot(cr_tot_diff,type='l')
pr<-periodogram(cr_tot_diff)
prspec<-sort(pr$spec,decreasing=TRUE)
f_1<-pr$freq[which(pr$spec==prspec[1])]  ##第一个周期频率
f_2<-pr$freq[which(pr$spec==prspec[2])]  ##第二个周期频率

3.模型拟合

#生成衍生变量，谱分析拟合
gydf<-data.frame(id=c(1:length(cr_tot_diff)),indexdata=cr_tot_diff)
gydf$v1_cos<-cos(2*pi*f_1*gydf$id)
gydf$v1_sin<-sin(2*pi*f_1*gydf$id)
gydf$v2_cos<-cos(2*pi*f_2*gydf$id)
gydf$v2_sin<-sin(2*pi*f_2*gydf$id)

#线性拟合
tt<-lm(formula=indexdata ~ v1_cos+v1_sin+v2_sin,data=gydf)
summary(tt)   ##R^2接近1，拟合效果较好

#拟合图
plot(as.vector(cr_tot_diff),type='l')
lines(fitted(tt),col="blue")

4.残差分析

#残差图
res<-tt$residuals  #计算残差
plot(tt,which=1)  #残差图  近似水平，无规律
library(car)
durbinWatsonTest(tt)   #DW独立性检验，p-value>0.05，符合独立性假设。
#同方差性
library(car)
ncvTest(tt)  ##p-value>0.05，符合同方差性。
shapiro.test(res)   #正态性检验

#预测上下限
#节假日第一天预测值
id_pre<-1
v1_cos_pre1<-cos(2*pi*f_1*id_pre)
v1_sin_pre1<-sin(2*pi*f_1*id_pre)
v2_sin_pre1<-sin(2*pi*f_2*id_pre)

pre_point<-data.frame(v1_cos=v1_cos_pre1,v1_sin=v1_sin_pre1,v2_sin=v2_sin_pre1)
hol.pred <- predict(tt,pre_point,interval = 'prediction',  level = 0.95) 
lcl_hol<-hol.pred[,'lwr']
ucl_hol<-hol.pred[,'upr']

#节假日范围=非节假日预测范围+节假日预测范围  ？
lcl_holtot<-lcl_ar[1]+lcl_hol
ucl_holtot<-ucl_ar[1]+ucl_hol

根据节假日模型预测节假日第一天数值的上下限，再加上非节假日模型预测的节假日第一天数值的上下限，两者总和就是节假日第一天预测值的上下限。模型也需要周期的检测，根据实际情况调参。