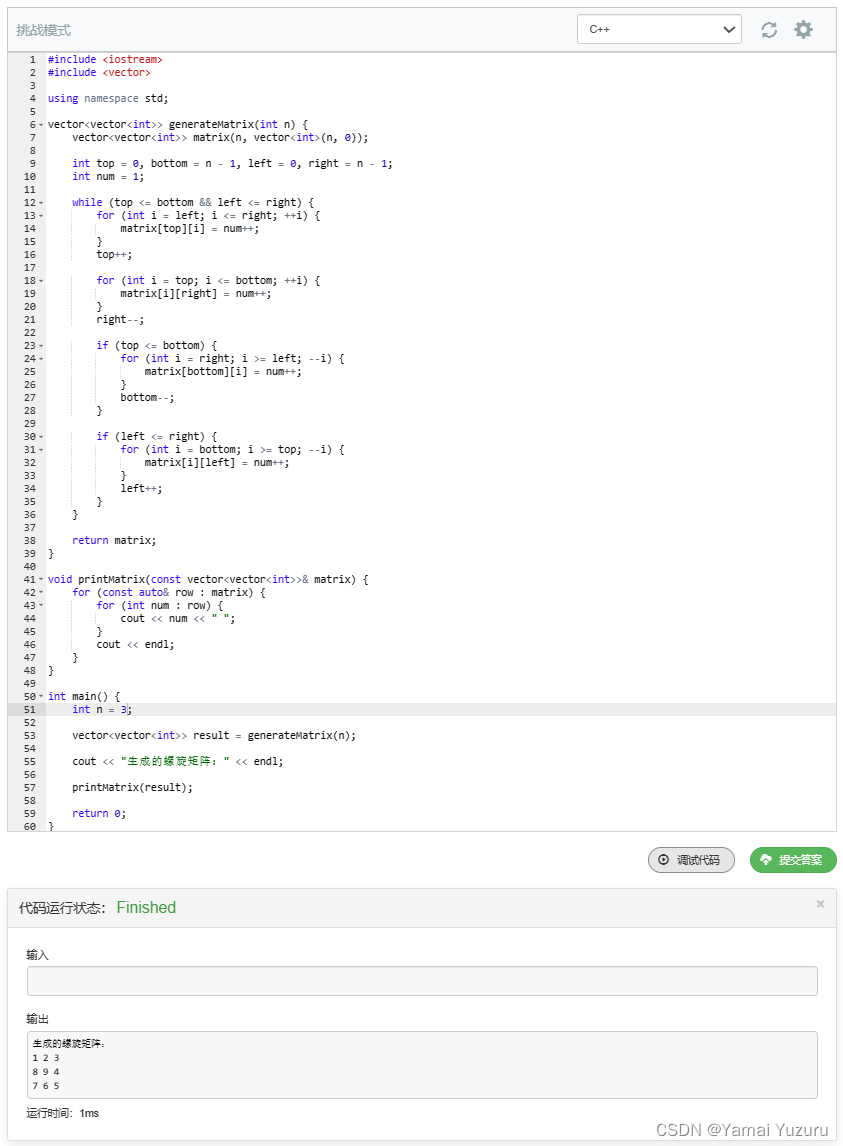
算法练习-螺旋矩阵（思路+流程图+代码）

难度参考

难度：中等

分类：数组

难度与分类由我所参与的培训课程提供，但需要注意的是，难度与分类仅供参考。以下内容均为个人笔记，旨在督促自己认真学习。

题目

        给定一个正整数n，生成一个包含1到 n^2 所有元素，且元素按【顺时针】顺序螺旋排列的正方形矩阵。
示例1:
        输入：n=3
        输出：[[1,2,3]，[8,9,4]，[7,6,5]]

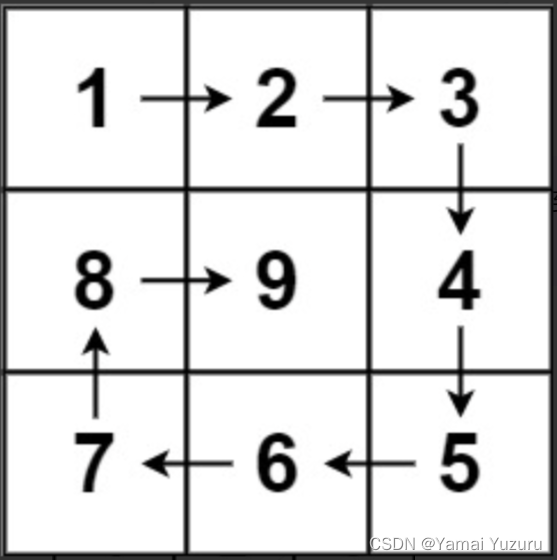
思路

题目要求生成一个顺时针螺旋排列的正方形矩阵，矩阵元素从1到n^2逐个递增。

初始化矩阵： 创建一个大小为n×n的矩阵，初始化所有元素为0。
定义边界： 使用四个变量top、bottom、left、right表示当前螺旋的边界。
顺时针填充矩阵： 使用循环，按照从左到右、从上到下、从右到左、从下到上的顺序填充矩阵。
更新边界： 每填充完一个方向后，更新相应的边界，确保下一轮填充在新的边界内进行。
重复步骤3和4： 循环执行步骤3和4，直到矩阵填充完成。

示例

考虑n=3的情况，即生成一个3×3的螺旋矩阵。

1.初始化矩阵：matrix = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]，

matrix = [
  [0, 0, 0],
  [0, 0, 0],
  [0, 0, 0]
]

初始边界：top=0, bottom=2, left=0, right=2。

2.从左到右：matrix[0][0]=1, matrix[0][1]=2, matrix[0][2]=3，

matrix = [
  [1, 2, 3],
  [0, 0, 0],
  [0, 0, 0]
]

更新top=1，

此时，top=1, bottom=2, left=0, right=2。

3.从上到下：matrix[1][2]=6, matrix[2][2]=9，

matrix = [
  [1, 2, 3],
  [0, 0, 4],
  [0, 0, 5]
]

更新right=1，

此时，top=1, bottom=2, left=0, right=1。

4.从右到左：matrix[2][1]=8, matrix[2][0]=7，

matrix = [
  [1, 2, 3],
  [0, 0, 4],
  [7, 6, 5]
]

更新bottom=1，

此时，top=1, bottom=1, left=0, right=1。

5.从下到上：matrix[1][0]=4，

matrix = [
  [1, 2, 3],
  [8, 9, 4],
  [7, 6, 5]
]

更新left=1，

此时，top=1, bottom=1, left=1, right=1。

在每个方向上填充完后，我们更新相应的边界，并按照新的边界进行下一个方向的填充。这样，直到矩阵被填充完成。

梳理

本题主要逻辑是生成一个顺时针螺旋矩阵，其本质是通过模拟顺时针填充矩阵的过程。

初始化矩阵和边界指针：
- 创建一个大小为 n x n 的矩阵，所有元素初始化为0。
- 初始化四个指针 top、bottom、left、right 分别表示矩阵的上、下、左、右边界。
- 初始化 num 用于填充矩阵的数字。
循环填充矩阵：
- 在满足循环条件的情况下，按照顺时针的顺序从左到右、从上到下、从右到左、从下到上依次填充矩阵。
- 在每个方向上，通过循环将 num 递增并填充到相应的位置。
逐步调整边界指针：
- 每填充完一个方向后，逐步调整边界指针，确保下一次填充的方向不会重叠。
返回生成的矩阵：
- 循环结束后，生成的矩阵即为顺时针螺旋矩阵。

本质上，这段代码通过模拟顺时针填充矩阵的过程，利用循环和边界指针的调整，逐步生成顺时针螺旋矩阵。这是一种常见的矩阵操作，通过巧妙的控制循环和边界指针，实现了一个相对简洁而高效的算法。

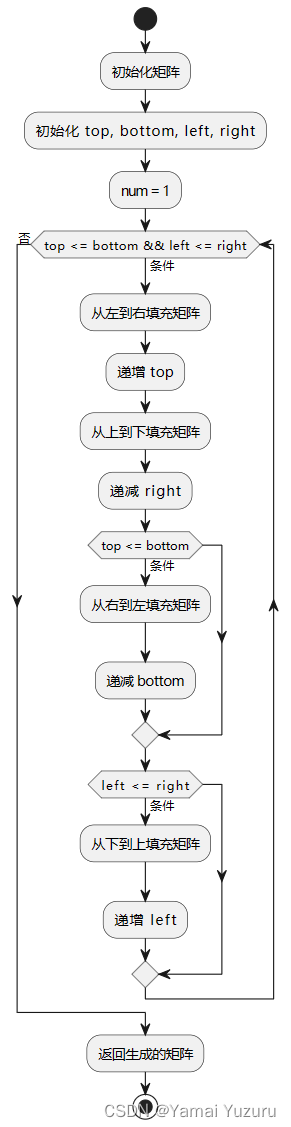
代码

#include <iostream>
#include <vector>

using namespace std;

// 生成顺时针螺旋矩阵
vector<vector<int>> generateMatrix(int n) {
    // 初始化矩阵
    vector<vector<int>> matrix(n, vector<int>(n, 0));

    // 设置边界指针
    int top = 0, bottom = n - 1, left = 0, right = n - 1;
    int num = 1; // 用于填充矩阵的数字

    // 循环填充矩阵
    while (top <= bottom && left <= right) {
        // 从左到右
        for (int i = left; i <= right; ++i) {
            matrix[top][i] = num++;
        }
        top++;

        // 从上到下
        for (int i = top; i <= bottom; ++i) {
            matrix[i][right] = num++;
        }
        right--;

        // 从右到左
        if (top <= bottom) {
            for (int i = right; i >= left; --i) {
                matrix[bottom][i] = num++;
            }
            bottom--;
        }

        // 从下到上
        if (left <= right) {
            for (int i = bottom; i >= top; --i) {
                matrix[i][left] = num++;
            }
            left++;
        }
    }

    return matrix;
}

// 辅助函数：打印矩阵
void printMatrix(const vector<vector<int>>& matrix) {
    for (const auto& row : matrix) {
        for (int num : row) {
            cout << num << " ";
        }
        cout << endl;
    }
}

int main() {
    int n = 3;
    
    // 生成螺旋矩阵
    vector<vector<int>> result = generateMatrix(n);

    cout << "生成的螺旋矩阵：" << endl;
    
    // 打印矩阵
    printMatrix(result);

    return 0;
}

时间复杂度：O(n^2)模拟过程相当于遍历了一遍二维矩阵。
空间复杂度：O(1)

难度参考

题目

思路

示例

梳理

代码

打卡