看书标记【R语言数据分析项目精解:理论、方法、实战 6】
看书标记——R语言
【R语言数据分析项目精解:理论、方法、实战】
Chapter 6 变量筛选技术
6.1项目背景、目标和方案
6.1.1项目背景
对底层数据做一次清洗和olap层中间数据的搭建,方便日后分析和选取。问题的提出:哪些变量是相关的?这些变量能否归类?
在统计建模中,筛选变量是前期最重要的步骤,原因:
(1)能提高魔性的稳定性
(2)能提高模型的预测能力
(3)能提高模型的运行效率
设计一套方法、开发一套程序以应对今后的变量筛选问题是有必要的, 可以给业务带来更好的解释和指引,帮助查看重要变量。发起一个内部技术项目:智能化筛选和划分变量。
6.1.2项目目标
(1)基于原始变量,探究各变量之间的关系
(2)开发变量筛选的通用模块
(3)规范变量变换和变量筛选流程。
6.1.3项目方案
(1)用变量相关系数,探究变量的相关性。
(2)对变量进行分析(变量筛选:距离聚类、模糊聚类等,从原始数据及中选出子集;变量降维:主成分分析、因子分析等,通过属性间的关系以组合的方式得到新的属性,改变了原本的特征空间)
(3)总结各方法的特点和使用情况,制作智能化工具。
6.2项目技术简介
(1)有较高缺失值的变量。缺失率大于阈值80%
(2)变量大部分为常数。逻辑变量除外
(3)变量站位过多,邮政编码类的变量需考虑剔除。
以上三种数据考虑直接剔除,然后将变量分为连续型和离散型,为下一步分析做准备。
6.2.1变量相关性
1.定类变量和定类变量
λ相关系数:用定类变量解释或预测定类变量时,以众数作为标准,这样可以减少预测误差。

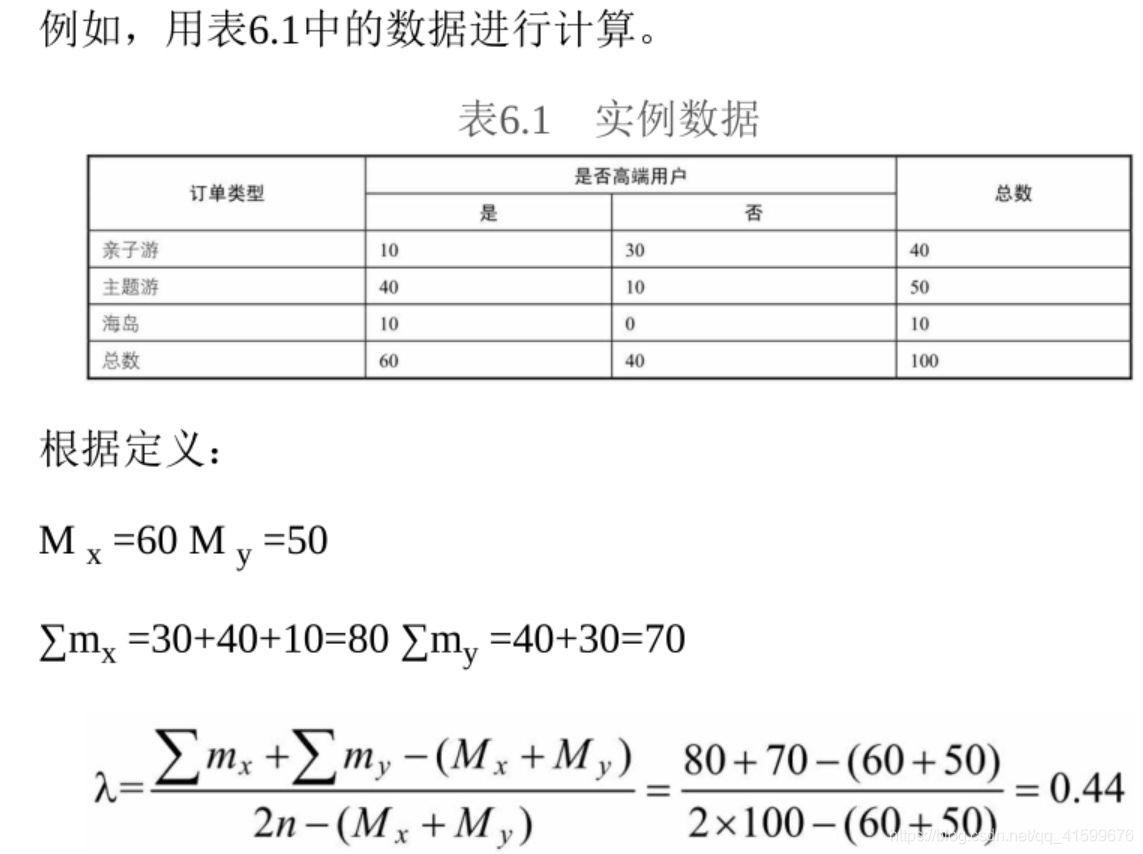
2.定序变量与定类变量
关于属性值的顺序之分
- 同序对:某对样本在两个变量上的相对等级是相同的
- 异序对:某对样本在两个变量上的相对等级是不同的
- 同分对:两个样本在某个变量上是同分。
(1)Gamma相关系数
G = ( N s − N d ) / ( N s + N d ) , N s 表示同序对, N d 表示异序对 G=(N_s-N_d)/(N_s+N_d),N_s表示同序对,N_d表示异序对 G=(Ns−Nd)/(Ns+Nd),Ns表示同序对,Nd表示异序对
( N s + N d ) (N_s+N_d) (Ns+Nd)表示在预测或解释任何一个个案的相对等级时可能的最大误差, ( N s − N d ) (N_s-N_d) (Ns−Nd)表示以一对个案在一个变量上的相对等级来预测其在另一个变量上的相对等级所能减少的误差。
(2)肯德尔的tau系数
有三种形式:tau-a、tau-b、tau-c。都可用于分析对称关系 (两个变量都是自变量,非对称关系是指两个变量一个是自变量一个是因变量),用于计算同序对数与异序对数之差在全部可能对数中所占的比例。
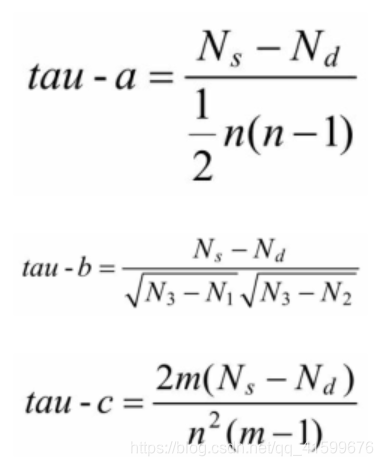
三种方法的适用情形: - 两变量没有同分对,tau-a
- 有同分对,交叉分组表行列数相等(r=c),tau-b
- 无论同分对和行列数,tau-c
(3)斯皮尔曼rho系数(等级相关系数)
不仅区分个案在两变量上的等级高低,还能将差异的确切数值计算出来。该算法可以消减误差比例:
r s = 1 − 6 ∑ D 2 n ( n 2 − 1 ) , D r_s=1- \frac {6\sum D^2}{n(n^2-1)},D rs=1−n(n2−1)6∑D2,D为同一个样本不同变量之间的等级差
3.定距(连续型)变量与定距变量
两个连续型变量之间的关系可以用斯皮尔曼相关系数来描述:
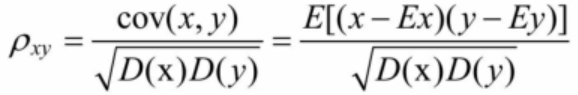
4.定类变量与定序变量
lambda、tau-y系数描述。
6.2.2变量筛选
1.基于变量距离的层次聚类
首先计算各变量之间的距离,然后根据变量之间的距离进行聚类,变量距离的计算基于变量相关性,变量相关性越高,它们之间的距离就越近;反之,它们之间的距离就越远。距离和相关性之间的关系如下:
D
x
y
=
1
−
ρ
x
y
D_{xy}=1-ρ_{xy}
Dxy=1−ρxy
根据聚类所用的不同方法,聚类可分为层次聚类、动态聚类、模糊聚类、基于密度聚类和最大期望聚类等。常会选择层次聚类和模糊聚类这两种。
变量层次聚类的步骤是:先计算变量之间的距离,每次将距离最近的点合并到同一个类;然后计算类与类之间的距离,将距离最近的类合并为一个大类;不停地合并,直到合成一个类。其中,类与类距离的计算方法有最短距离法、最长距离法、中间距离法和类平均法等。比如,最短距离法是将类与类的距离定义为类与类之间变量的最短距离,最长距离法是将类与类的距离定义为类与类之间变量的最长距离。
2.基于变量距离的模糊聚类
在现实生活中,事物的分类往往是模糊不清、没有明显界线的。对于此类聚类问题,就需要我们借助模糊数学的理论并结合传统意义上的聚类分析方法,得到一个新的聚类方法——模糊聚类。
6.2.3变量降维
1.主成分分析(PCA)
将众多原始变量变为少数几个相互独立的线性组合形成的变量(主成分),线性组合后的的主成分方差变得最大,使得主成分之间显示出最大的个别差异性。
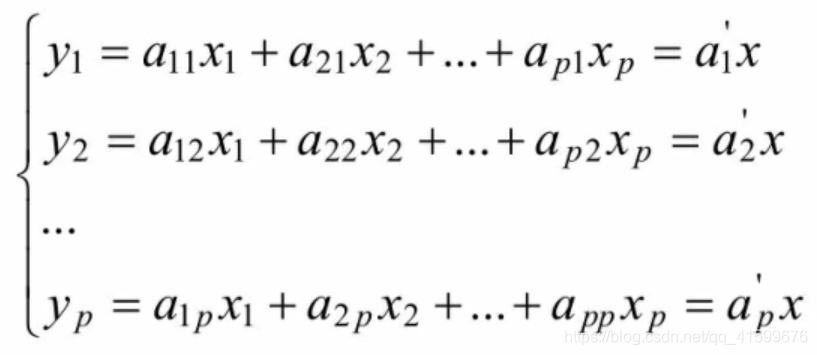
其中系数a要满足
V
(
y
1
)
=
a
1
′
∑
a
1
V(y_1)=a_1'\sum a_1
V(y1)=a1′∑a1最大,此时对应第一主成分,还希望达到,
c
o
v
(
y
1
,
y
2
)
=
0
cov(y_1,y_2)=0
cov(y1,y2)=0.
在提取主成分后,新的主成分变量可能不太容易解释,为了尽可能地对新变量去噪,可采用主成分旋转来完成。常用的主成分旋转有两种:正交旋转(使选择的成分仍旧保持不相关,常用的正交旋转为方差极大旋转,它试图使载荷矩阵每列只有少数几个很大的载荷,其他都是很小的载荷)和斜交旋转(使选择的成分变得相关)。
2.因子分析
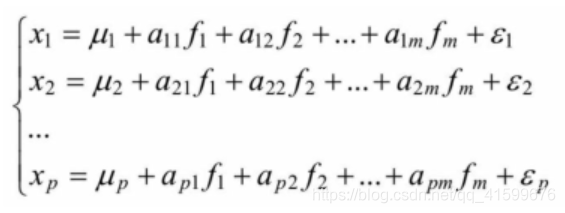
6.2.4 R语言实例代码
1.基于变量距离的层次聚类
(1)计算变量相关性
cor(x,y=NULL,method=‘pearson’) ##‘pearson、kendall、spearman’
(2)层次聚类
hclust(d,method) ##d为dist类数据类型,可以用as.dist()转换。向量的内积作为距离,默认为欧氏距离。层次聚类方法有:single(最短距离法)、complete(最长距离法)、median(中间距离法)、mcquitty(相似法)、average(类平均法)、centroid(重心法)和ward.D(离差平方和法)
#函数功能:依据变量相似性利用层次聚类法进行聚类
#df:原始数据,必须为数据框
#k:需要聚类的个数(可以先随便设定,然后逐步调整)
varcluster_hc<-function(mydf,k,method='average'){
cordist<-as.dist(1-cor(mydf)) #计算变量相关性,并转换成距离对象
hcl<-hclust(cordist,method) #对距离进行层次聚类
plclust(hcl,hang=-1) #画出树状图
rel<-rect.hclust(hcl, k, border="red") #用红框画出分类的效果
varnames<-c() #输出变量类别
for (i in 1:length(rel)){
varnames<-c(varnames,names(rel[i][[1]]))
}
classid<-rep(1:k,unlist(lapply(rel,length)))
varclass<-data.frame(varname=varnames,corclass=classid)
return(varclass)
}
varcluster_hc(mtcars,3) #用mtcars数据为例,分成3类,可以用碎石图等方法确定需要聚成几类
步骤为,先计算变量相关系数》计算距离并转换为dist类型调用hclust函数》生成树状图》输出变量分类结果
2.模糊聚类
#函数功能:根据相关系数矩阵,利用模糊聚类方法实现变量聚类
#mydf:原始数据,必须为数据框类型
#class_level:设定lamda的值,取值范围:-1~1.随着lamda的值越大,聚类的个数也越大。
library(plyr)
fuzzycluster<-function(mydf,class_level){
#模糊矩阵合成
fuzzycombine<-function(fmatrix){
n<-nrow(fmatrix)
rresmatrix<-matrix(,n,n)
for (i in 1:n){
for (j in 1:n){
rresmatrix[i,j]<-max(pmin(fmatrix[i,],fmatrix[,j]))
}
}
return(rresmatrix)
}
#计算模糊等价关系
fuzzyequal<-function(fmatrix){
n<-length(fmatrix)
r_1<-fmatrix
i<-0
num<-1
while(i==0){
r_2<-fuzzycombine(r_1)
if(sum(r_1==r_2)/n==1){
i<-1
} else{
r_1<-r_2
num<-num*2
}
}
return(list(r_1,num))
}
#根据模糊等价关系得到的截矩阵,进行聚类
classcluster<-function(r_lamda_loc){
blist<-list()
blist_num<-1
while(nrow(r_lamda_loc)!=0){
r_first<-unique(unlist(r_lamda_loc[1,]))
bl_f<-r_first
bl_t<-c()
bl_2<-c()
rowmatch_l<-c()
while(length(bl_f)!=0){
for (i in 1:length(bl_f)){
rowmatch<-which(r_lamda_loc==bl_f[i],arr.ind=TRUE)[,1]
bl<-unique(unlist(r_lamda_loc[rowmatch,]))
bl_2<-unique(c(bl_2,bl))
bl_t<-unique(c(bl_t,bl_f[i]))
rowmatch_l<-unique(c(rowmatch_l,rowmatch))
}
if(length(rowmatch_l)!=0){
r_lamda_loc<-r_lamda_loc[-rowmatch_l,]
}
rowmatch_l<-c()
bl_f<-bl_2[!(bl_2%in%bl_t)]
if(length(bl_f)==0 | nrow(r_lamda_loc)==0){
blist[[blist_num]]<-bl_2
blist_num<-blist_num+1
break
}
}
}
return(blist)
}
if(class_level>=1){
message("pls input class_level lower than 1!")
}
#计算相关矩阵
cormatrix<-cor(mydf)
#输出变量及对应的id
varname<-attributes(cormatrix)[[2]][[1]]
id<-c(1:length(varname))
vardf<-data.frame(varname=varname,id=id)
#计算模糊相似矩阵
fuzzysimilarmatrix<-(1+cormatrix)*0.5
#计算模糊等价关系
fuzzy_matrix<-fuzzyequal(fuzzysimilarmatrix)
res_lamda<-fuzzy_matrix[[1]]>class_level
#计算模糊聚类
r_lamda_loc<-as.data.frame(which(res_lamda == 1 & lower.tri(res_lamda,diag=TRUE) == 1, arr.ind = TRUE))
blist<-classcluster(r_lamda_loc)
#把模糊聚类结果和变量整合,最终输出变量聚类结果
varlist<-c()
classlist<-c()
for (i in 1:length(blist)){
varnum<-blist[[i]]
class<-rep(i,length(varnum))
varlist<-c(varlist,varnum)
classlist<-c(classlist,class)
}
class_res<-data.frame(id=varlist,fuzzyclass=classlist)
fuzzyres<-join(vardf,class_res)
return(fuzzyres)
}
根据模糊等价关系得到截矩阵》聚类》贪婪算法每次解决一个类别的变量聚类》循环
3.主成分分析
principal(x,nfactor=主成分个数,rotate=旋转方法(默认为最大方差旋转varimax),scores=F是否需要计算主成分得分)
library(psych)
pca_eigen<-function(df,cumproplevel=0.85){ ##cumproplevel:主成分累计贡献方差阈值
corrx<-cor(df) #计算相关矩阵
colnum<-length(df) #原始向量变量个数
eigenresult<-eigen(corrx) #求相关矩阵特征值和特征向量
eigenvalue<-eigenresult$values #求相关矩阵特征值
eigenvector<-eigenresult$vectors
plot(eigenvalue,type='b',main='Eigen for the Data') #画碎石图
abline(h=1,col='blue')
prop.eigen<-eigenvalue/colnum #计算每个主成份的方差贡献率
cum.prop<-cumsum(prop.eigen) #计算累计方差贡献率
#判断达到累计贡献方差阀值的主成份个数
if(sum(cum.prop<=cumproplevel)==0){
tsprint<-paste("第一主成份方差贡献超过",cumproplevel*100,'%',sep='')
principal_cnt<-1
} else
{
tsprint<-paste(sum(cum.prop<=0.85)+1,"个主成份方差累计贡献超过",cumproplevel*100,'%',sep='')
principal_cnt<-sum(cum.prop<=0.85)+1
}
#创建结果矩阵
iocomponents<-matrix(rep(0,3*colnum),nrow=3,ncol=colnum)
iocomponents[1,]<-eigenvalue
iocomponents[2,]<-prop.eigen
iocomponents[3,]<-cum.prop
rowname<-c("eigenvalue","prop.eigen","cum.prop")
colname<-c()
for(i in 1:colnum){
colname<-c(colname,paste("comp",i,sep=''))
}
dimnames(iocomponents)<-list(rowname,colname)
#整个结果到一个列表输出
result<-list(主成份情况=tsprint,主成分个数=principal_cnt,主成份结果=iocomponents,特征向量=eigenvector)
return(result)
}
#用原始数据作为输入,得到主成分个数
setwd("C:\\Users\\用户路径")
pca<-read.csv("pcatest.csv",header=TRUE,stringsAsFactors=FALSE)
pca_index<-pca_eigen(pca)
##碎石图判断主成分个数
###关于主成分旋转
#用相关矩阵作为输入
pc<-principal(Harman23.cor$cov, nfactors=2,rotate='none')
pc
#用方差极大旋转法(它试图对载荷阵的列进行去噪,使得每个成分只是由一组有限的变量来解释)
rc<-principal(Harman23.cor$cov, nfactors=2,rotate="varimax")
rc
#输出主成分得分
round(unclass(rc$weights),2)
PC1:成分载荷,指观测变量与主成分的相关系数,成分载荷可用来解释主成分的含义。
h2:成分公因子方差,即主成分对每个变量的方差解释度。
u2:成分唯一性,即方差无法被主成分解释的比例(1-h2)。
SS loadings:与主成分相关联的特征值,指的是与特定主成分相关联的标准化后的方差值(在本例中,第一主成分的值为4.67)。
Proportion Var:每个主成分对整个数据集的解释程度。此处可以看到,第一主成分解释了58%的方差。
PC1=0.28height+0.3arm.span+0.3forearm+0.28lower.leg-0.06*weight(数值为标准化后的数据)
##关于主成分的R函数
########### prcomp函数 ################
#prcomp函数是对变量矩阵(相关矩阵)采用SVD方法计算其奇异值(原理上是特征值的平方根),函数帮助中描述为函数结果中的sdev。prcomp函数输入参数为变量矩阵(x),center中心化 默认为true,scale标准化 默认为false,建议改为true,rank主成份个数。prcomp函数输出有sdev(各主成份的奇异值),rotation(特征向量,回归系数),x(score得分矩阵)。
iris.pca<-prcomp(iris[,-5],scale=T,rank=4,retx=T) #相关矩阵分解
#scale表示要标准化,retx表四返回score
summary(iris.pca) #方差解释度
iris.pca$sdev #特征值的开方 ,平方后代表的是每个主成分可以解释的数据差异
iris.pca$rotation #特征向量,回归系数
iris.pca$x #样本得分score
#princomp函数:princomp以计算相关矩阵或者协方差矩阵的特征值为主要手段。princomp函数输出有主成份的sd,loading,score,center,scale.
data(wine) #三种葡萄酿造的红酒品质分析数据集
wine.pca<-princomp(wine,cor=T,scores=T)
#默认方差矩阵(cor=F),改为cor=T则结果与prcomp相同
summary(wine.pca) #各主成份的SVD值以及相对方差
wine.pca$loading #特征向量,回归系数
wine.pca$score
screenplot(wine.pca) #方差分布图
biplot(wine.pca,scale=F) #碎石图,直接把x与rotation绘图,而不标准化
详细的Rcode可以看R语言 PAC分析与可视化.
4.因子分析
library(psych)
mtc<-mtcars[,c(1,3,4,5,6,7)] #获取数据
corr<-cor(mtc) #计算相关矩阵
ss<-fa.parallel(corr,n.obs=30,fa="both",n.iter=100) #平行法碎石图
1<-ss$nfact #确定因子个数
factanal(mtc,factors=factornum,rotation = 'varimax') #正交旋转 因子之间独立
factanal(mtc,factors=factornum,rotation = 'promax') #斜交旋转 因子之间相关性
fa<-factanal(mtc,factors=1,rotation = 'promax',scores = "regression")
fa$scores #斜交旋转且输出因子得分
loadings为因子载荷矩阵,p-value对应的原假设为H0:两因子是充分的。也可以用于判断因子个数的选择合理性。
6.3项目实践
6.3.1变量筛选
#导入测试数据
tot<-read.csv(“运营指标数据.csv”)
tot_df<-tot[,-1]
#执行层次聚类和模糊聚类
corres<-varcluster_hc(tot_df,5)
fuzzyres<-fuzzycluster(tot_df,0.885)
#整合两种聚类效果
varclust<-join(fuzzyres[,-2],corres)
varclust[order(varclust
c
o
r
c
l
a
s
s
,
v
a
r
c
l
u
s
t
corclass,varclust
corclass,varclustfuzzyclass),]
##根据聚合的情况结合实际业务分析得到这些指标中最具代表性、业务上最容易解释的,制作起来最方便的指标即可。
6.3.2变量降维
1.主成分分析
library(psych)
tot<-read.csv("运营指标数据.csv")
tot_df<-tot[,-1]
#根据前面分类效果,初步变量筛选
var<-c('fltorderamount','ordercnt_outland',
'ordercnt_atoutland','pship_uv','pgroup_uv',
'ios_active','ordercnt','htlordercnt','trnordercnt',
'ttdordercnt','actordercnt','uv' ,'uv_h5','fn_uv',
'hn_uv','act_uv','bus_uv','pticket_uv','train_uv',
'total_uid','active'
)
tot_res<-tot_df[,var]
#得到主成分个数
pca_eigen(tot_res)
#用方差极大旋转法得到主成分得分
rc<-principal(tot_res,nfactors=4,rotate="varimax")
#输出主成分得分
round(unclass(rc$weights),2)
PC1=-0.06orderamount-0.01ordercnt_outland-0.12*ordercnt_atoutland
……
2.因子分析
library(psych)
corr<-cor(tot_res) #计算相关矩阵
ss<-fa.parallel(corr,n.obs=30,fa="both",n.iter=100) #平行法碎石图
factornum<-ss$nfact #确定因子个数
factanal(tot_res,factors=factornum,rotation = 'varimax') #正交旋转 PC actual data
factanal(tot_res,factors=factornum,rotation = 'promax') #斜交旋转 FA actual data
#用斜交旋转,并输出因子得分(由平行碎石图判断选取方法)
fa<-factanal(tot_res,factors=factornum,rotation = 'promax',score="regression")
fa$score