编译原理设计:自下而上的编译器,(C++实现)

各位好,这次分享的是编译原理课程中的自下而上的编译器设计,在这之前,我在本站分享过自下而上LR分析程序的完整代码,见此链接:自下而上的语法分析(LR分析程序)
但那个程序只能分析加法和乘法运算,且无法分析大于一个字符的运算变量,在这个程序中,对于以上问题进行了完善,但为了方便采用了算符优先分析,至于LR的分析各位有兴趣可以看上面那篇文章进行参考。
目录
一、写在前面
1.本人并不擅长编程,各位可以交流学习,如果有错误欢迎指出。
2.不保证思路和解决方式是最佳思路,也不能保证正确性,请勿将本文当做考试复习参考。其中涉及到专业名词的部分可能会有描述错误,请谅解。
3.本人个人写代码不习惯写注释,变量的命名也很随意,请谅解。
4.本文会讲述全部代码思路,代码需要自己整合,仅作为交流。
5.请谅解文章中的错别字,标点符号,以及的地得!
二、功能需求
本编译器完成了一下需求:
任务:编写一个完整的编译程序,包括词法分析器、语法分析器以及实现对简单程序设计语言中
的逻辑运算表达式、算术运算表达式、赋值语句、While语句,并生成中间代码。
具体如下:
1) 可以输入要编译的文件名,从给定文件中读取编译的源程序,也可从键盘输入;
2) 能进行功能选择进行词法分析,语法分析,中间代码生成,输出
3) 可以输出二元式序列,分析过程,四元式表;
4) 语法分析给出分析过程,分析结果。
5) 以自下而上方法实现语法分析
三、需求分析
根据题目要求,要实现词法分析,语法分析,中间代码生成,三个要求,这三个要求相辅相成,词法分析能保住语法分析,语法分析的结果也能够为中间代码生成提供输入,且输入需满足逻辑运算表达式、算术运算表达式、赋值语句、While语句。
在这里我们提供的输入形式也要满足两个要求:输入要编译的文件名,从给定文件中读取编译的源程序,从键盘输入。
同时要照顾到三个不同的测试数据,分别为1、全部合法数据;2、整体非法数据;3、局部非法数据。
四、详细过程
这里我们按照步骤来对每一个模块进行相应地说明。
4.1输入
输入我们放在Word类中的fileopen()函数中。这里不光满足了题目要求中两种方式,我们还内置了一个范例语句:
main(){
int A=0,B=1,C=1,D=2;
while(!A && C>D){
C=(A+B*D)*C;
}
}
这个范例语句包含了题目的所有要求:逻辑运算表达式、算术运算表达式、赋值语句、While语句。
在fileopen()中,我们根据用户的选择读入输入的语句,而内置的范例语句其实也是放在文件中的。如果用户不选择输入地址就会默认采用范例语句所在文件的地址。

接下来,无论是以哪种方式,我们都要把输入的语句放在数组K中,便于后续操作,这里如果是采用从键盘输入时需要注意,因为输入空格会被cin识别成两个语句,而int后面必须要加一个空格(不然int无法被识别成标识符)。所以在这里要有一个特例进行讨论:

代码如下:
void word::fileopen() {
char str[100][101];
char a[100];
int i = 1, Fun, line;
FILE* file;
h = 0;
cout << "******************************自下而上编译器******************************" << endl;
cout << "\t\t请进行选择输入语句的方式:" << endl;
cout << "\t\t(1)从文件中导入" << endl;
cout << "\t\t(2)直接输入" << endl;
cout << "\t\t(3)使用内置范例语句" << endl << endl;;
cout << "\t\t请输入对应序号或输入(0)退出:";
cin >> Fun;
if (Fun == 0) exit(0);
if (Fun == 2) {
cout << "\t\t请输入语句总行数:";
cin >> line;
for (int li = 1; li <= line; li++) {
cout << "\t\t";
cin >> k[li];
if (k[li] == "int") {//如果输入了int
string abc;
cin >> abc;
k[li] = k[li] + " " + abc;//把int后面的语句和空格加到前面
}
h++;
}
system("cls");
return;
}
else if (Fun == 1) {
cout << "\t\t请输入文件地址:";
cin >> a;
file = fopen(a, "r");
}
else file = fopen("C:\\Users\\Desktop\\test.txt", "r");//范例语句的文件地址
if (file == NULL) {
printf("打开文件失败!!!");
exit(0);
}
else {
while (fgets(str[i], 100, file) != NULL) {
k[i] = str[i];
i++;
h++;
}
}
system("cls");
}4.2词法分析
来到词法分析,这里我们通过两个判断字符和数字的函数加上原来语句中的空格对输入的语句进行拆分。

这里数字和单词的判断方式是一样的,逐个保存字符,只要下一个字符的类型和上一个不符合,就把当前字符送到对应的函数中判断。

那么剩下没有被字母和数字判断到的就是类似“(”,“)”这样的界符和运算符,我们在系统中提前存放了界符,运算符和系统标识符,剩下的符号就可以单独进行函数判断。
在这里,其实每个单词符号的拆分工作就已经完成了,我们可以顺便把这些拆分好的单词符号放在数组everyword中。

这里我顺便考虑了两个事情,第一个是如果用户没用定义自变量生成的报错,如当输入以下语句时:
main(){
while(A<B && C<D){
C=(A+B*D)*C;
}
}
这里ABCD都没有定义,自然是要报错的,这里想到的,由于定义的变量肯定是在符号“int”和“;”中间(int 语句;),所以我可以自定义一个信号量,当遍历到“int”时打开,遍历到“;”时关闭,在信号量打开时保存所有出现的自变量,而在信号量关闭时,如果出现的自变量没有被保存则报错。
![]()


第二个事情是出现“++”时,如何保证不被判断为两个“+”号。这里呢,我是首先在遇到符号时优先两个符号的匹配,如果两个符号匹配失败再进行一个符号匹配。

接下来的每个判断函数其实都差不多这里只挑字符(单词)的进行说明:
在单词判断中,程序会先判断是否为关键字,即单词是否在数组KEY中,若不是才会到用户变量名ID数组中再次比较,都不是后才会在ID数组中新建一个变量名。


这里还顺便承担了前面提到的定义报错的功能,我们要在出现错误的时候中断程序标记出错的位置。

这样我们的词法分析就完成了。这里我们分别用1-5表示,系统标识符,自定义变量,数字,运算符,界符。
而系统标识符,运算符和界符被我们存在了word类的构造函数中,如下:
word::word() {
//输入关键字、运算符和界符表
this->key[0] = "int";
this->key[1] = "char";
this->key[2] = "float";
this->key[3] = "void";
this->key[4] = "const";
this->key[5] = "if";
this->key[6] = "else";
this->key[7] = "do";
this->key[8] = "while";
this->key[9] = "scanf";
this->key[10] = "printf";
this->key[11] = "return";
this->key[12] = "main";
this->key[13] = "read";
this->cla[0] = "+";
this->cla[1] = "-";
this->cla[3] = "*";
this->cla[4] = "/";
this->cla[5] = "%";
this->cla[6] = "=";
this->cla[7] = "==";
this->cla[8] = ">";
this->cla[9] = "<";
this->cla[10] = "!=";
this->cla[11] = ">=";
this->cla[12] = "<=";
this->cla[13] = "&&";
this->cla[14] = "||";
this->cla[15] = "!";
this->cla[16] = "<>";
this->cla[17] = "++";
this->cla[18] = "--";
this->lin[0] = '(';
this->lin[1] = ')';
this->lin[2] = '{';
this->lin[3] = '}';
this->lin[4] = ';';
this->lin[5] = ',';
this->lin[6] = '\"';
this->lin[7] = '\'';
this->lin[8] = '[';
this->lin[9] = ']';
this->a = 0;
this->b = 0;
this->h = 0;
this->numw = 0;
this->flag = 0;
this->numok = 0;
this->intymy = 0;
}相关代码如下:
词法分析函数:
void word::cifafenxi() {
int j = 0;//flag是判断当前自变量有没有被定义
string ww;
for (int high = 1; high <= h; high++) {
for (int i = 0; i < k[high].length(); i++)
{
if (letterjudge(k[high][i])) {
j++;//一直是字母就一直加
if (not letterjudge(k[high][i + 1])) {//下一个不是字母就结束了
wordjudge(k[high].substr(i - j + 1, j));//到单词判断函数去判断是系统标识符还是用户自定义变量
ww = k[high].substr(i - j + 1, j);
j = 0;
if (ww != "\n") {
numw++;
everyword[numw] = ww;
if (ww == "int") intymy = 1;//打开信号量
}
}
}
else if (number(k[high][i])) {
j++;
if (not number(k[high][i + 1])) {//下一个不是数字就结束了
numberjudge(k[high].substr(i - j + 1, j));
ww = k[high].substr(i - j + 1, j);
j = 0;
if (ww != "\n") {
numw++;
everyword[numw] = ww;
}
}
}
else if (else1(k[high][i]) && k[high][i] != ' ') {
if (finjudge(k[high].substr(i, 2))) {//如果两个能被匹配就按两个算
ww = k[high].substr(i, 2);
i++;//for循环本身+1,这里取了两位所以要多加一位
if (ww != "\n") {
numw++;
everyword[numw] = ww;
}
}
else {
finjudge(k[high].substr(i, 1));//如果两个不能被匹配就按一个算
ww = k[high].substr(i, 1);
if (ww != "\n") {
numw++;
everyword[numw] = ww;
}
}
}
}
}
}单词判断函数:
void word::wordjudge(string k) {
flag = 0;
int flag1;
int f = 0;
char str[5] = { 0 };
for (int i = 0; i <= 20; i++)
{
if (k == key[i]) {//在系统定义标识符中
itoa(i + 1, str, 10);
result[numw + 1] = k + ":<1," + str + ">";
label[numw + 1] = 1;
flag = 1;
}
}
flag1 = 0;
if (flag == 0) {
if (intymy == 1) {
intok[numok] = k;//信号量打开时,保存所有的自变量
numok++;
}
for (int i = 0; i < numok; i++) {
if (k == intok[i]) flag1 = 1;//如果有定义flag1就是1
}
if (flag1 == 0) {//flag1=0,没有定义
jincase = 1;//错误为1
jin = k;//k是函数的输入参数,就是说k未被定义
return;
}
for (int i = 1; i <= a; i++) {
if (k == id[i]) {//之前定义的时候存了
itoa(i, str, 10);
result[numw + 1] = k + ":<2," + str + ">";
label[numw + 1] = 2;
f = 1;
}
}
if (f == 0) {//现在是定义的时候
a++;
id[a] = k;
itoa(a, str, 10);
result[numw + 1] = k + ":<2," + str + ">";
label[numw + 1] = 2;
}
}
}数字判断函数:
void word::numberjudge(string k) {
const char* p = k.c_str();//数字和字符串的转换
char str[5] = { 0 };
int t = atoi(p);
flag = 0;
for (int i = 1; i <= b; i++) {
if (t == ci[i]) {
itoa(i, str, 10);
result[numw + 1] = k + ":<3," + str + ">";
label[numw + 1] = 3;
flag = 1;
}
}
if (flag == 0) {
b++;
ci[b] = t;
itoa(b, str, 10);
result[numw + 1] = k + ":<3," + str + ">";
label[numw + 1] = 3;
}
}运算符判断函数:
bool word::finjudge(string k) {
char str[5] = { 0 };
flag = 0;
for (int i = 0; i < 20; i++) {
if (cla[i] == k) {
itoa(i + 1, str, 10);
result[numw + 1] = k + ":<4," + str + ">";
label[numw + 1] = 4;
flag = 1;
if (flag == 1 && k.length() == 2) return true;
else return false;//返回运算符有几个字符,两个返回真
}
}
}界符判断函数:
这里由于界符和运算符都不是字母或数字,但是界符只有一个字符,所以在判断上,我们是先判断界符,如果当前字符是界符才返回假,如果词法分析得到的结果是真,那么我们才进行运算符判断。这里真假倒过来是为了方便后续代码少写一个not。

bool word::else1(char k) {
char str[5] = { 0 };
flag = 0;
string ww;
for (int i = 0; i < 10; i++) {
if (lin[i] == k) {
itoa(i + 1, str, 10);
flag = 1;
ww = k;
result[numw + 1] = ww + ":<5," + str + ">";
label[numw + 1] = 5;
if (ww != "\n") {
numw++;
everyword[numw] = ww;
if (ww == ";") {
intymy = 0;//关闭信号量
}
}
}
}
if (flag == 0) return true;
else return false;
}4.3语法分析
在词法分析阶段,我们把每一个不同的语法元素按类拆分放在了数组everyword中,我们接下来就可以利用这个数组进行语法分析,由于题目的要求是自下而上,我们这里采用算符优先的方法。这一部分位于clacu()类中。
我们先在类中存放好所有运算会用到的产生式,如下:

这里按优先级从上至下分布,函数flit()用来分离文法,在分离文法时,利用“->”和“|”做判断符,将前者a与后者yuan[i]做链接形成单独的文法,将产生式的非终结符,终结符,单个产生式分别保存,便于日后使用。产生的结果放在数组w[]中,非终结符和终结符分别保存在数组VN[]和VT[]。
但这里会遇到一个问题,就是“||”运算和产生式的分隔符冲突了,所以我们在根据“|”进行拆分时,要看看后一位是否也是“|”避免或运算被当成分隔符被拆分。结果位于数组w0中。

同时,和词法分析一样,我们也要排除在储存终结符时诸如把“==”号当成两个“=”储存的情况。好在我们这次的运算中会出现偏差的只有“==”,“||”,“!=”这三个符号,我们只要拿出来单独讨论一下就好了。

这里两个字符的运算符am就被加了两次,防止终结符的数组VT就不会有误。
完整代码如下:
void clacu::flit() {//分离文法
string a, a1;
int k = 0, j, flag, am = 1;
x = 0;
for (int i = 0; i < n; i++) {
for (j = 0; j < id[i].length(); j++) {
if (id[i].substr(j, 2) == "->") {
a = id[i].substr(0, j + 2);
a1 = id[i].substr(0, j);
k = j + 2;
VN[x] = id[i].substr(0, j);
x++;
}
if (id[i].substr(j, 2) == "||") {//防止或运算被拆分
j = j + 2;//跳过这两个符号(j是循环变量)
}
if (id[i].substr(j, 1) == "|") {//根据“|”符号进行拆分
yuan[n1] = id[i].substr(k, j - k);//yuan是表达式箭头后面的部分
gui[n1] = a1;//gui是表达式箭头前面的部分
w[n1] = a + yuan[n1];
k = j + 1;
n1++;
}
}
gui[n1] = a1;//这一部分和第二个if一样,因为后面的产生式没有“|”结尾
yuan[n1] = id[i].substr(k, j - k);
w[n1] = a + id[i].substr(k, j - k);
n1++;
}
for (int i = 0; i < n; i++) {//这个循环是为了保存产生式中的终结符
for (j = 3; j < id[i].length(); j++) {
flag = 0;
for (int p = 0; p < x; p++) {
if (id[i].substr(j, 1) == VN[p] || id[i].substr(j - 1, 2) == "->") {
//防止“->”和非终结符被放入
flag = 1;
break;
}
if (id[i].substr(j, 1) == "|") {//防止“|”被放入
flag = 1;
break;
}
}
for (int p = 0; p < t; p++) {
if (id[i].substr(j, 1) == VT[p]) {//排除重复
flag = 1;
break;
}
}
if (id[i].substr(j, 2) == "||" || id[i].substr(j, 2) == "==" || id[i].substr(j, 2) == "!=") {
flag = 0;
//如果是这三种也要判断,因为“==”可能会因为“=”弄过了然后排除(前面有个排除重复)
}
if (flag == 0) {
am = j;
while (flagVN(id[i].substr(am, 1))) {//如果是终结符
am++;
if (id[i].substr(am - 1, 2) == "||") {
//这里怕误判,或运算要单独考虑,am+2规避下面“|”作为分隔符的判断
am++;
}
if (am >= id[i].length()) break;//防止溢出
if (id[i].substr(am, 1) == "|") break;
//这里的“|”表示的是结束的“|”,因为上面或我们am加了两次
}
VT[t] = id[i].substr(j, am - j);
j = am;
t++;
}
}
}
}此外这里的flagVN函数用来判断当前字符是否为终结符,是终结符返回TRUE。Copy函数用来复制两个数组,将前面参数的数组复制到后面参数对应的数组。
具体如下:
bool clacu::flagVN(string a){
for(int k=0;k<x;k++){
if(a==VN[k]) {
return false;
}
}
return true;
}在制作firstvt集中,通过判断箭头后的第一个字符是否为非终结符和终结符前的第一个字符是否为非终结符进行判断。(第一个if和第二个if)

完成后进行遍历,若发现该非终结符可以归约为另外一个非终结符,则将其所有的firstvt集赋值给另外的非终结符,Copy函数用来复制两个数组,将前面参数的数组复制到后面参数对应的数组。

lastvt集的做法与之类似,这里就不解释了。
firstvt和lastvt的函数如下:
void clacu::fvt() {
int num, num1[10] = { 0 };
int flag, f = 2, j;
for (int i = 0; i < n1; i++) {
j = 0;
while (w[i].substr(j, 2) != "->") j++;
for (int k = 0; k < x; k++) {
if (w[i].substr(0, j) == VN[k]) num = k;
}
f = j + 2;//为下面复制定位
for (j = 0; j < numw0[i]; j++) {
if (j != numw0[i] - 1) {//不是最后一个
if (flagVN(w0[i][j])) {
firstvt[num][num1[num]] = w0[i][j];
num1[num]++;
number1[num] = num1[num];
}
}
if (j == numw0[i] - 1 && j == 0) {//最后一个但是开头
if (flagVN(w0[i][j])) {
firstvt[num][num1[num]] = w0[i][j];
num1[num]++;
number1[num] = num1[num];
}
}
}
}
for (int i = n1 - 1; i >= 0; i--) {
for (int j = 0; j < numw0[i]; j++) {
if (j == numw0[i] - 1 && j == 0) {//如果只有一个
if (not flagVN(w0[i][j])) {//且是非终结符
copy1(w[i].substr(0, f - 2), w0[i][j]);//f在上面定位,是→出现的位置
}
}
}
}
}void clacu::lvt() {
int num, num1[10] = { 0 };
int flag, f = 2, j;
for (int i = 0; i < n1; i++) {
j = 0;
while (w[i].substr(j, 2) != "->") j++;
for (int k = 0; k < x; k++) {
if (w[i].substr(0, j) == VN[k]) num = k;
}
f = j + 2;
for (j = 0; j < numw0[i]; j++) {
if (j > 0) {
if (flagVN(w0[i][j])) {
lastvt[num][num1[num]] = w0[i][j];
num1[num]++;
number2[num] = num1[num];
}
}
if (j == 0 && numw0[i] == 1) {
if (flagVN(w0[i][j])) {
lastvt[num][num1[num]] = w0[i][j];
num1[num]++;
number2[num] = num1[num];
}
}
}
}
for (int i = n1 - 1; i >= 0; i--) {
for (int j = 0; j < numw0[i]; j++) {
if (j == numw0[i] - 1 && j == 0) {
if (not flagVN(w0[i][j])) {
copy2(w[i].substr(0, f - 2), w0[i][j]);
}
}
}
}
}接着就可以通过firstvt集和lastvt集制作优先关系表,这里的flag1,flag2,flag3分别表示当前符号的后,前以及当前符号是否为终结符,是为1,非为0,然后根据书本上的内容,用0,1,-1表示大小关系(2表示没有,即无法归约)。

这里的四个if分别对应书上的四条规则:
- 1.当前和后一个符号为终结符,置=;
- 2.前一个符号和后一个符号为终结符,当前为非终结符,置前一个符号=后一个符号;
- 3.当前为终结符,后一个符号为非终结符,置当前符号<后一个符号的firstvt集所有元素;
- 4.当前为非终结符,后一个符号为终结符,置当前符号的lastvt集所有元素>后一个元素;

而在C语言中是存在特例的(书本上是用Pascal 作为例子 如while A do B end 正好是一个终结符一个非终结符,而我们的C语言中while(A){B},这里的(A)会和算术运算的(A)混淆所以我定义为了while A {B},所以“while”,“(”相邻的情况没有考虑到,同样的像int A;while…… 中“;”和“while”也没有考虑到,所以全部要分开考虑,这波要在程序最后手动添加)

这段的完整代码如下:
void clacu::makelist() {
int flag1, flag2, flag3;
for (int i = 0; i < n1; i++) {
for (int j = 0; j < numw0[i] - 1; j++) {
flag1 = 0;
flag2 = 0;
flag3 = 0;
for (int p = 0; p < t; p++) {
if (w0[i][j + 2] == VT[p]) {
flag1 = 1;
}
if (w0[i][j + 1] == VT[p]) {
flag3 = 1;
}
if (w0[i][j] == VT[p]) {
flag2 = 1;
}
}
if (flag2 == 1 && flag3 == 1) {//当前和后一个符号位终结符,置=
list[number(w0[i][j], 1)][number(w0[i][j + 1], 1)] = 0;//0表示相等
}
if (j < numw0[i] - 2 && flag1 == 1 && flag2 == 1 && flag3 == 0) {//j要注意别越界
//前一个符号和后一个符号为终结符,当前为非终结符,置前一个符号=后一个符号
list[number(w0[i][j], 1)][number(w0[i][j + 2], 1)] = 0;//0表示相等
}
if (flag3 == 0 && flag2 == 1) {
//当前为终结符,后一个符号为非终结符,置当前符号<后一个符号的firstvt集所有元素
for (int k = 0; k < number1[number(w0[i][j + 1], 0)]; k++) {
list[number(w0[i][j], 1)][number(firstvt[number(w0[i][j + 1], 0)][k], 1)] = -1;//-1表示小于
}
}
if (flag3 == 1 && flag2 == 0) {
//当前为非终结符,后一个符号为终结符,置当前符号的lastvt集所有元素>后一个元素
for (int k = 0; k < number2[number(w0[i][j], 0)]; k++) {
list[number(lastvt[number(w0[i][j], 0)][k], 1)][number(w0[i][j + 1], 1)] = 1;//1表示大于
}
}
}
}
list[number("#", 1)][number(";", 1)] = 0;
list[number(")", 1)][number("{", 1)] = 1;
list[number("{", 1)][number(";", 1)] = 0;
list[number("(", 1)][number(";", 1)] = 0;
list[number("(", 1)][number("!", 1)] = 0;
list[number(";", 1)][number("i", 1)] = 1;
list[number("!", 1)][number("i", 1)] = 0;
list[number(";", 1)][number("}", 1)] = 1;
list[number("int", 1)][number(";", 1)] = 1;
list[number(";", 1)][number("while", 1)] = 1;
list[number("int", 1)][number("while", 1)] = 1;
}同时这里出现的number函数介绍一下,number函数是用来返回当前字符在某个表中的位置,整个表是根据参数来定的,这个在之前那篇文章中也解释过。

最后就是归约:
在归约之前我们要对语句进行整理,首先我们没有设计main的归约,所以要把main的部分去除,其次,要给每个语句的前后加上“#”作为开始和结束的标志,最后语句中出现的所有用户自定义变量,我们要转换为“i”,以便于程序识别(F→i)。
这里我们做了两手准备,用两个数组str1和str2,str1是给用户看的,用户自定义变量保持不变,而str2是给程序运作的,自定义变量转换为了“i”所以guiyue函数才有两个输入参数。

这里用两个数组作为栈用作归约,a,b两个数组分别为guiyue函数的参数。

循环关系最初设置为死循环,结束的条件为当前比较的字符和当前字符都为“#”,根据优先关系表中的(0,1,-1,即大于归约,等于移进,小于报错)
而判断归约项具体是哪一项,这里我的方法是,因为前面生成式中每个生成项的运算符是不一样的,所以我们可以根据每次归约的运算符来判断到底需要用哪一项来进行归约。这里要考虑到几种特殊情况,我们一种一种来看。
首先是会出现连续的语句如:
A=A+1;
B=B+1;
如果我们归约的话只能归约为AA(A→A=T T→E E→E+B,按这三个顺序),这样如果语句太长我们最后的归约项也会很复杂,所以我们可以把这些连续的赋值语句全部归约为一项,但是要注意,此项的开头不能是“int”,也就是fr=“;”,i=“i”。

其次,当我们完成一次归约后,由于场面上会一直存在一项,会对后续的判断产生误差,例如:
对于语句#int A; while……归约完成int后,就变为#Wwhile……下一次比较时由于W是最终归约项,没被删除,所以就会从原本该有的“#”和“while”变为“W”和“while”出现错误。
这里我想到有两种方法,一是增加一个全局变量偏移值,每次完成归约就增加一个偏移值,二是直接把系统识别的str1第二个位置变成“#”也就是把归约完的语句变为##while……,反正我们输出的是str2的内容,前面归约完了也不会影响后面的归约,这里为了简单方便我用了第二种方法。

第三就是“!”(非)的情况,因为非的运算符是在开头所以比较的时候fr会变成后面的i,所以这里要手动标记一下。

最后,如果出现无法归约的情况(优先表中没有内容),我们要像刚才int报错一样传回报错的变量信号。

虽然到这里其实已经基本完成了,但是为了下一步中间代码生成的方便,我们这里把每次归约的归约项记录下来(因为归约的顺序就是我们运算的顺序)传给第三模块的函数。

这里由于语法分析的类clacu是继承自编译模块生成的program类的,所以我们可以直接在归约的函数中调用编译模块生成的主要函数bianyi()。
![]()
规约部分的代码如下:
void clacu::guiyue(string a[], string b[]) {
for (int j = 0; j < n1; j++) {
for (int i = 0; i < numw0[j]; i++) {
for (int p = 0; p < t; p++) {
if (w0[j][i] == VT[p] && VT[p] != "#") {
cla[j] = VT[p];
break;
}
}
}
}
cout << endl;
string i, x[50], x1[50], x2[50], y, fr, i1, icase;
int k = 1, gg, numx = 0, mou(0);
string out;
x1[numx] = a[0];//完成的部分
x2[numx] = b[0];
numx++;//当前的位置
fr = a[0];//当前比较的第一个非终结符
i = a[1];//当前比较的第二个非终结符
i1 = b[1];
result[0] = left(x2, 0, numx) + nul(left(x1, 0, numx), left(b, k, length)) + left(b, k, length);
numresult++;
while (1) {
if (list[number(fr, 1)][number(i, 1)] == -1 || list[number(fr, 1)][number(i, 1)] == 0) {
x1[numx] = i;
x2[numx] = i1;
numx++;
fr = i;
k++;
i = a[k];
i1 = b[k];
result[numresult] = left(x2, 0, numx) + nul(left(x2, 0, numx), left(b, k, length)) + left(b, k, length) + " 移进";
numresult++;
}
else if (list[number(fr, 1)][number(i, 1)] == 1) {
string st;
if (x1[numx - 2] == "!") st = "!";
else st = fr;
for (gg = 0; gg < n1; gg++) {
if (cla[gg] == fr) {
break;
}
}
if (fr == "i") icase = x2[numx - 1];//如果是i要转换为原来的样子
for (int suibianla = 0; suibianla < numw0[gg]; suibianla++) {
if (fr == "i" && suibianla == numw0[gg] - 1) gui_yue[numguiyue][suibianla] = icase;
gui_yue[numguiyue][suibianla] = x2[numx - numw0[gg] + suibianla];
}
if (fr == ";" and i == "i" and x1[numx - 3] != "int") {
numx = numx - 3;//往前倒三步干脆把这段删了 E;i numx现在位于i;
fr = x1[numx];
}
else {
numx = numx - numw0[gg];
x1[numx] = gui[gg];
x2[numx] = gui[gg];
fr = x1[numx - 1];
}
if (cla[gg] == "int") {
mou = mou + 1;//int结束修改一次
}
if (cla[gg] == "while") {
mou = mou + 1;//while结束修改一次
}
for (int iu = 0; iu <= mou; iu++) {
x1[iu] = "#";
}
numx++;
result[numresult] = left(x2, 0, numx) + nul(left(x2, 0, numx), left(b, k, length)) + left(b, k, length) + " 规约 " + w[gg];
numresult++;
label_guiyue[numguiyue] = w[gg];
bianyi(label_guiyue[numguiyue], gui_yue[numguiyue]);
numguiyue++;
}
else {
jincase = 2;
break;
}
if (i == "#" && fr == "#") {
result[numresult] = "结果为:";
for (int ke = 0; ke <= mou; ke++) result[numresult] = result[numresult] + x2[1 + ke];
numresult++;
break;
}
}
}4.4中间代码生成
这里其实程序基本上可以说已经是完成了,编译模块非常简单,只要根据书上的代码和每个运算对应的逻辑来就可以了。
这里要做说明,因为非运算只有一个参与运算的变量,所以和与运算和或运算分开讨论,由于C语言中逻辑运算只会出现在括号里,所以我们括号里的运算就用作真出口的判断,while语句,可以得知假出口的位置,所以用作假出口的判断。

我们一个一个来看,首先是赋值运算:
赋值运算很简单,只需要栈里面吐两个值出来然后用等号连接即可。这里quaternion的0-3分别代表四元式的每个位置的值。

完整代码如下(其实上面就是完整代码):
void program::equalop() {
quaternion[numq][0] = "=";
quaternion[numq][1] = stack[numstack - 1];//吐一个
quaternion[numq][2] = "-";
quaternion[numq][3] = stack[numstack - 2];//吐两个
numq++;
numstack = numstack - 2;//栈指针移动
}然后是算术运算,大体上和等号运算一样,栈里吐两个值,但栈的两个值要存到寄存器中,还要最后把寄存器压回栈中。所以寄存器的编号要设为全局变量,每次加一。

完整代码如下:
void program::arithop(string a) {
if (markingflag == 0) {//这里的marking会在下文中解释
marking = numq;
markingflag = 1;
}
string Re;
char str[5] = { 0 };
itoa(Rnum, str, 10);
Re = "T" + std::string(str);
quaternion[numq][0] = a;
quaternion[numq][1] = stack[numstack - 1];//吐一个
quaternion[numq][2] = stack[numstack - 2];//吐两个
quaternion[numq][3] = Re;//寄存器
numq++;
numstack = numstack - 2;//栈指针移动
stack[numstack] = Re;//寄存器压到栈里
numstack++;//栈指针移动
Rnum++;//寄存器编号+1
}比值运算就是在四元式最后一个位置要标记为真出口和假出口,所以多了一列,在这里我们先标记为0,等到逻辑运算时再标记真假出口。同样,这里也要从栈里吐两个值。

完整代码如下:
void program::ratioop(string a) {
if (markingflag == 0) {
marking = numq;
markingflag = 1;
}
string J;
J = "j" + a;
quaternion[numq][0] = J;
quaternion[numq][1] = stack[numstack - 1];//吐一个
quaternion[numq][2] = stack[numstack - 2];//吐两个
quaternion[numq][3] = "0";//真出口
numq++;
quaternion[numq][0] = "j";
quaternion[numq][1] = "-";
quaternion[numq][2] = "-";
quaternion[numq][3] = "0";//真出口
numq++;
numstack = numstack - 2;//栈指针移动
}非运算,非运算较为简单,由于是单纯地倒过来(假才成立),所以我们把第一个出口设为假出口(名义上的假),第二个设为真,这也解释了为什么我们在刚刚比值运算的时候不直接写出口的真假了。
但是要注意,非运算只有一个预算的变量,这个变量有可能是用户输入的也有可能是寄存器中的,由于我们之前归约时将E→!F统一归约了,这里对于自定义变量没有压入栈的环节了,所以这里需要判断一下是否为自定义变量。

完整代码如下:
void program::notop(string a) {
if (markingflag == 0) {
marking = numq;
markingflag = 1;
}
string J, Re;
char str[5] = { 0 };
J = "j!";
quaternion[numq][0] = J;
itoa(Rnum - 1, str, 10);
Re = "T" + std::string(str);
if (numstack > 0 && stack[numstack - 1] == Re) {//是寄存器就从栈里吐出来
quaternion[numq][1] = stack[numstack - 1];
numstack = numstack - 1;
}
else {//不然就直接写用户自定义变量
quaternion[numq][1] = a;
}
quaternion[numq][2] = "-";
quaternion[numq][3] = "f";
quaternion[numq + 1][0] = "j";
quaternion[numq + 1][1] = "-";
quaternion[numq + 1][2] = "-";
quaternion[numq + 1][3] = "t";
numq = numq + 2;
}剩下的逻辑运算,与运算和或运算由于这里的不同性,我们要分开讨论。
首先是与运算,当第一个表达式判断为真时,还要继续判断,如果假就跳转假出口,如果第二个表达式为真则跳转真出口,假同样为假出口,所以第一个表达式真出口的地址其实是第二个表达式,这时我们可以直接填入,其余的我们就按对应真假填写。
此外,我们还得考虑到非运算的真假是倒转的,所以针对非运算还得单独开一条讨论,至于判断是不是“0”,是为了不影响非运算已经弄好的真假出口标记。

而对于或运算,当第一个表达式判断为真时,就可以直接判断为真出口了,如果假则还要继续判断,如果第二个表达式为真则也转真出口,假也就为假出口了,所以第一个表达式假出口的地址其实是第二个表达式,这里方法和前面与运算一样。这里同样也要考虑非运算的影响。

完整代码如下:
void program::logicop(string a) {
numq = numq - 4;
char str[5] = { 0 };
if (a == "&&") {
itoa(numq + 2, str, 10);
if (quaternion[numq][3] == "0" || quaternion[numq][3] == "t") quaternion[numq][3] = str;
//不是非运算的真出口,跳转下一个表达式
if (quaternion[numq + 1][3] == "t") quaternion[numq + 1][3] = str;//非运算的真出口,跳转下一个表达式
if (quaternion[numq + 1][3] == "0") quaternion[numq + 1][3] = "f";//假出口
numq = numq + 2;
if (quaternion[numq][3] == "0") quaternion[numq][3] = "t";//真出口
if (quaternion[numq + 1][3] == "0") quaternion[numq + 1][3] = "f";//假出口
numq = numq + 2;
}
if (a == "||") {
itoa(numq + 2, str, 10);
if (quaternion[numq][3] == "0") quaternion[numq][3] = "t";//真出口
if (quaternion[numq][3] == "f") quaternion[numq][3] = str;//非运算的假出口,跳转下一个表达式
if (quaternion[numq + 1][3] == "0" || quaternion[numq + 1][3] == "f") quaternion[numq + 1][3] = str;
//不是非运算的假出口,跳转下一个表达式
numq = numq + 2;
if (quaternion[numq][3] == "0") quaternion[numq][3] = "t";//真出口
if (quaternion[numq + 1][3] == "0") quaternion[numq + 1][3] = "f";//假出口
numq = numq + 2;
}
}到了括号判断真出口,括号表示这里的逻辑判断已经结束,真出口的位置其实就是下一条地址,但是这里要照顾到可能判断的语句中并没有出现逻辑运算,例如只是单纯地while(A>B)这时我们就要先按顺序先补上真假出口标记,然后再修改真出口为真正的真出口地址。

完整代码如下:
void program::Trueexit() {
char str[5] = { 0 };
itoa(numq, str, 10);
for (int i = 0; i < numq; i++) {
if (quaternion[i][3] == "0") {//先标记
quaternion[i][3] = "t";
quaternion[i + 1][3] = "f";
}
if (quaternion[i][3] == "t") quaternion[i][3] = str;//真出口是下一个语句
}
}最后是while判断假出口,这里假出口也简单,就是while的下一句。

但是由于while语句的特点,其实每次判断为运算完还是要返回到开始再次判断,所以while还是要在最下面再加上一个(j,-,-,0)最后的这个位置填的是while最开始的位置。
而如何找到开始的位置呢?我们在每次(运算的开头弄一个标记,如果标记是0,就在运算时置一),当出现“S→W;”或者是while结束时就把标记置0。也就是每个语句块结束时。

![]()
while部分的代码如下:
void program::whileop() {
char str[5] = { 0 };
itoa(marking, str, 10);
quaternion[numq][0] = "j";
quaternion[numq][1] = "-";
quaternion[numq][2] = "-";
quaternion[numq][3] = str;
markingflag = 0;
numq++;
itoa(numq, str, 10);
for (int i = 0; i < numq; i++) {
if (quaternion[i][3] == "f") quaternion[i][3] = str;//假出口是下一个语句
}
}这样,我们的所有程序就完成了。
最后把我们之前标记的错误报告打印一下就可以了。


五、测试与运行结果
这里我们一共用了三组数据分别是:



对于后面两组错误数据,程序分别能给出相应的错误判断,如下:


而对于正确数据,分别能输出题目要求的二元式序列,分析过程,四元式表,如下:

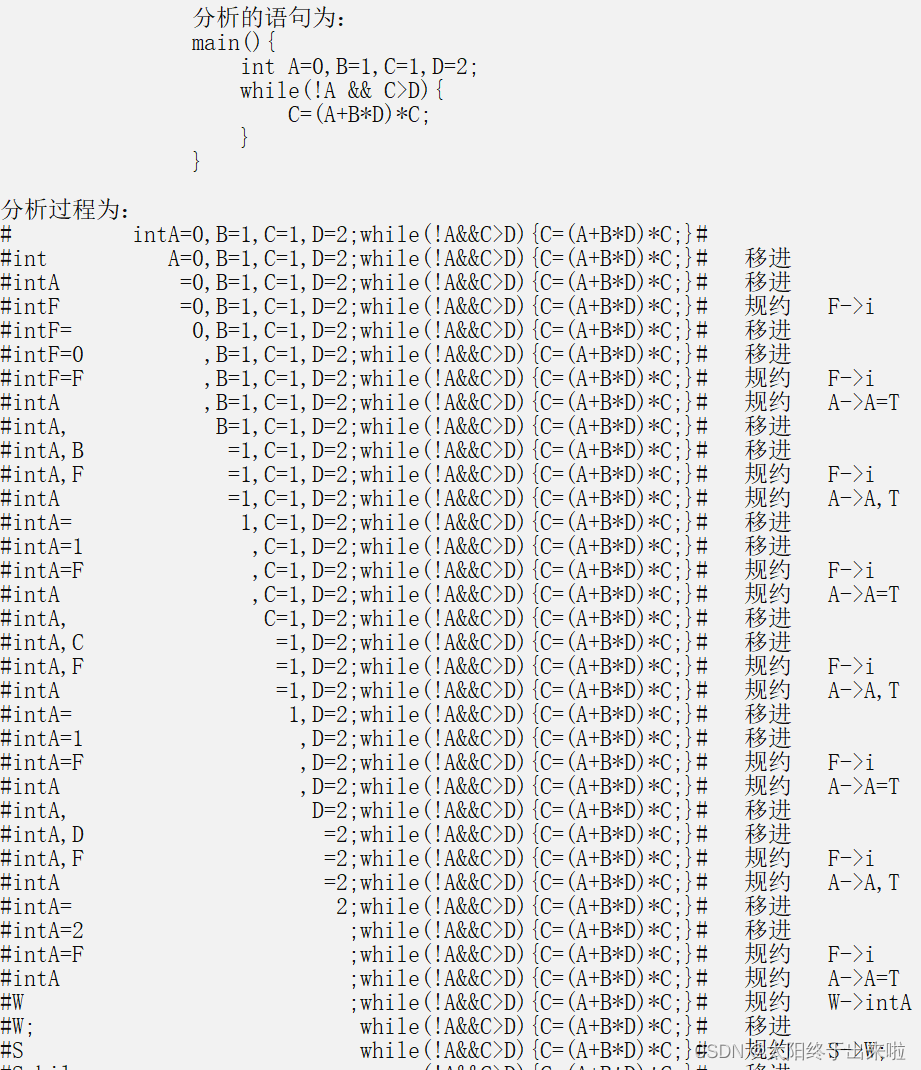
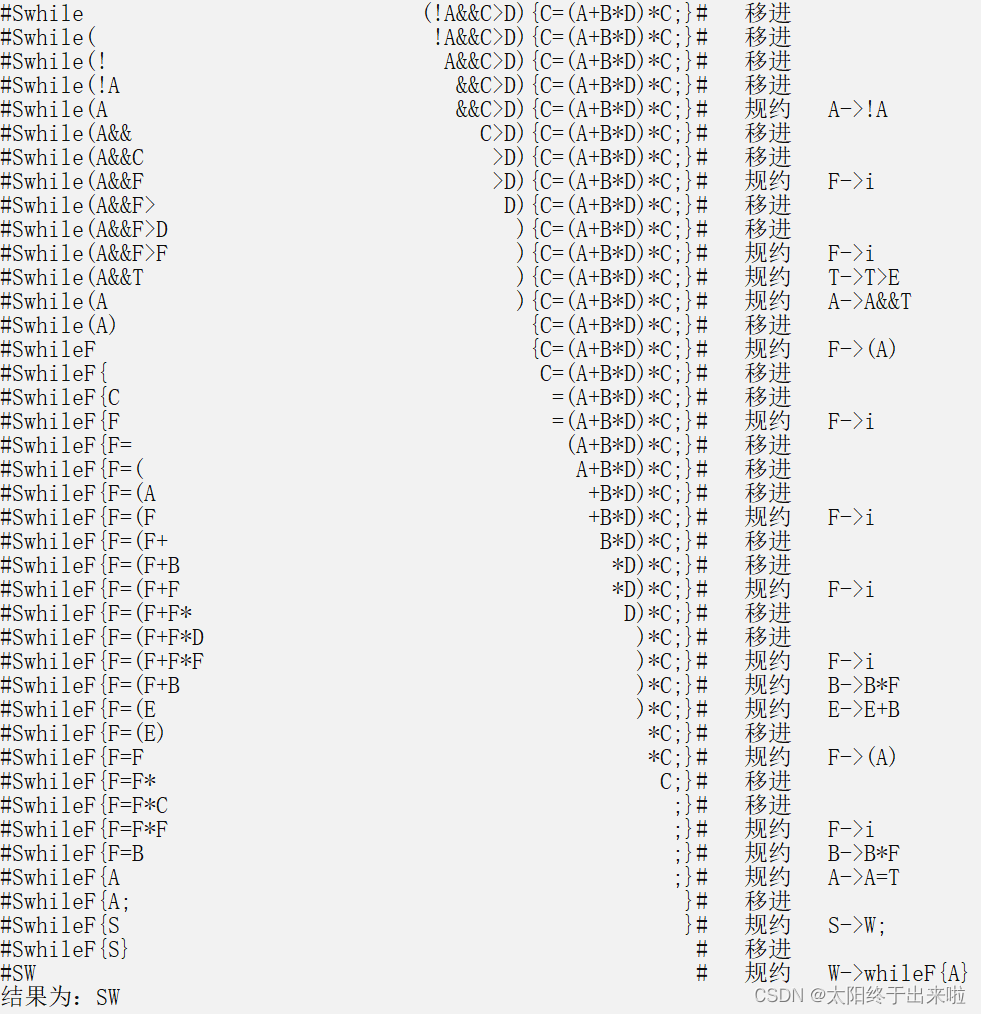

以上,这次由于做得比较多也比较辛苦,没有po出完整源代码,但是文章也基本展现了完整思路和近80%的代码,根据文章思路自己尝试复现也基本不会有问题。如果各位是在有需要源代码可以联系邮箱zggzgg@foxmail.com。
感谢你的时间