2021年经典大厂面试题——算法与数据结构版（含答案）

经典大厂面试题

在这里插入图片描述

题目

请问，Object作为HashMap的key的话，对Object有什么要求吗？
请问 hashset 存的数是有序的吗？
输入一个二叉树和一个整数，打印出二叉树中节点值的和等于输入整数所有的路径
二叉树的搜索区间
现在有一个单向链表，谈一谈，如何判断链表中是否出现了环
随机链表的复制
找出数组中和为S的一对组合，找出一组就行
求一个数组中连续子向量的最大和
谈一谈，如何得到一个数据流中的中位数？
你知道哪些排序算法，这些算法的时间复杂度分别是多少，解释一下快排？
请你解释一下，内存中的栈(stack)、堆(heap) 和静态区(static area) 的用法。
说一说，heap和stack有什么区别。
请你设计一个算法，用来压缩一段URL？
谈一谈，id全局唯一且自增，如何实现？
一个长度为N的整形数组，数组中每个元素的取值范围是[0,n-1],判断该数组否有重复的数，请说一下你的思路并手写代码
请问求第k大的数的方法以及各自的复杂度是怎样的，另外追问一下，当有相同元素时，还可以使用什么不同的方法求第k大的元素
判断一个链表是否为回文链表，说出你的思路并手写代码

答案

请问，Object作为HashMap的key的话，对Object有什么要求吗？

考察点：哈希表
参考回答：要求 Object 中 hashcode 不能变。
解读：什么是hashcode。Java语言中，Object对象有个特殊的方法：hashcode(), hashcode()表示的是JVM虚拟机为这个Object对象分配的一个int类型的数值，JVM会使用对象的hashcode值来提高对HashMap、Hashtable哈希表存取对象的使用效率。
关于Object对象的hashCode()返回值，网上对它就是一个简单的描述：“JVM根据某种策略生成的”.
什么是JVM。Java虚拟机（Java Virtual Machine 简称JVM）。通常来说，高级语言运行在不同的平台上，需要编译为不同的语言，但是如果不同的平台都有虚拟机，由虚拟机来执行Java语言，就不需要编译为不同的语言，这也就解释了为什么Java可以跨平台运行。

请问 hashset 存的数是有序的吗？

参考回答： Hashset 是无序的。
解读：什么事hashset。hashset储存的是唯一的对象，没有下标，只能通过增强for，或者迭代器进行遍历。当出现相同的对象，会合并，只储存一个空间。

//遍历方法一：
Iterator<news> it=set.iterator();
while(it.hasNext()){
	News n=it.next();
	
}
-----------------------------------------
//遍历方法二：
for(News n:set){
	printf(n);
}

输入一个二叉树和一个整数，打印出二叉树中节点值的和等于输入整数所有的路径

剑指Offer JZ24 二叉树中和为某一值的路径

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector<vector<int> > FindPath(TreeNode* root,int expectNumber) {
        vector<int> path;    
        vector<vector<int> >res;
        if(root==NULL)return res;
        Find(root,path,expectNumber,res);
        return res;
    }
    void Find(TreeNode* root,vector<int>& p,int sum,vector<vector<int>> &res){
        p.push_back(root->val);
        if(sum==root->val&&!root->left&&!root->right){
            res.push_back(p);
        }
        if(root->left)Find(root->left,p,sum-root->val,res);
        if(root->right)Find(root->right,p,sum-root->val,res);
        //回溯
        p.pop_back();
    }
};

二叉树的搜索区间

给定两个值 k1 和 k2（k1 < k2）和一个二叉查找树的根节点。找到树中所有值在 k1 到 k2 范围内的节点。即打印所有x (k1 <= x <= k2) 其中 x 是二叉查找树的中的节点值。返回所有升序的节点值。

利用中序遍历，得到节点值递增的数组。在从数组中选择满足条件的数。

现在有一个单向链表，谈一谈，如何判断链表中是否出现了环

LeetCode.141.环形链表

方法一：哈希

最容易想到的方法是
遍历所有节点，
每次遍历到一个节点时，判断该节点此前是否被访问过。
可以使用哈希表来存储所有已经访问过的节点。
每次到达一个节点的时候
判断：
如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。
重复这一过程，直到我们遍历完整个链表即可

方法二：快慢指针

设置一个快慢指针fast和slow，开始时slow和fast都指向链表的头节点head。然后slow每次移动一步（slow->next），fast每次移动两步（fast->next->next），在链表中遍历。
如果链表无环，fast指针在移动过程一定先遇到终点，到达终点的标志是（fast->next=NULL)(奇数个节点)||(fast->next->next=NULL（偶数个节点）），直接返回false，表示链表无环。
如果有环slow和fast一定会相遇，并且是在NULL第一个入环的节点处相遇（证明略），slow==fast直接返回true。

bool hasCycle(struct ListNode* head) {
    if (head == NULL || head->next == NULL) {
        return false;
    }
    struct ListNode* slow = head;
    struct ListNode* fast = head->next;
    while (slow != fast) {
        if (fast == NULL || fast->next == NULL) {
            return false;
        }
        slow = slow->next;
        fast = fast->next->next;
    }
    return true;
}

随机链表的复制

题目—leetcode138. 复制带随机指针的链表

解法一：使用hash存储原结点和克隆结点的映射关系，通过映射关系处理克隆结点的random指针。

代码一：java语言

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/

class Solution {
    public Node copyRandomList(Node head) {
        if(head == null){
            return head;
        }
        // map方法，空间复杂度O(n)
        Node node = head;
        // 使用hash表存储旧结点和新结点的映射---key:旧节点，val:新节点
        Map<Node,Node> map = new HashMap<>();
        while(node != null){
            Node clone = new Node(node.val,null,null);
            map.put(node,clone);
            node = node.next;
        }
        //第二次遍历
        node = head;
        while(node != null){
            //根据key旧节点，找到val新节点，完善next指针
            map.get(node).next = map.get(node.next);
            //根据key旧节点，找到val新节点，完善random指针
            map.get(node).random = map.get(node.random);
            //遍历指针后移
            node = node.next;
        }
        //根据旧节点，找到新节点
        return map.get(head);        
    }
}

代码二：cpp语言

class Solution {
public:
    Node* copyRandomList(Node* head) {
        unordered_map<Node*, Node*> link;
        Node* pNode = head;
        while (pNode != nullptr) {
            link[pNode] = new Node(pNode->val);
            pNode = pNode->next;
        }
        pNode = head;
        while (pNode != nullptr) {
            link[pNode]->next = link[pNode->next];
            link[pNode]->random = link[pNode->random];
            pNode = pNode->next;
        }
        return link[head];
    }
};

找出数组中和为S的一对组合，找出一组就行

类似LeetCode39题

LeetCode.39. 组合总和

从数组中找出所有组合为s的数

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

public class Solution {

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, res);
        return res;
    }

    /**
     * @param candidates 候选数组
     * @param begin      搜索起点
     * @param len        冗余变量，是 candidates 里的属性，可以不传
     * @param target     每减去一个元素，目标值变小
     * @param path       从根结点到叶子结点的路径，是一个栈
     * @param res        结果集列表
     */
    private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        // target 为负数和 0 的时候不再产生新的孩子结点
        if (target < 0) {
            return;
        }
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 重点理解这里从 begin 开始搜索的语意
        for (int i = begin; i < len; i++) {
            path.addLast(candidates[i]);

            // 注意：由于每一个元素可以重复使用，下一轮搜索的起点依然是 i，这里非常容易弄错
            dfs(candidates, i, len, target - candidates[i], path, res);

            // 状态重置
            path.removeLast();
        }
    }
}

求一个数组中连续子向量的最大和

谈一谈，如何得到一个数据流中的中位数？

你知道哪些排序算法，这些算法的时间复杂度分别是多少，解释一下快排？

请你解释一下，内存中的栈(stack)、堆(heap) 和静态区(static area) 的用法。

区:专门用来保存对象的实例(new 创建的对象和数组)，实际上也只是保存对象实例的属性值，属性的类型和对象本身的类型标记等，并不保存对象的方法（方法是指令，保存在Stack中）

1.存储的全部是对象，每个对象都包含一个与之对应的class的信息。(class的目的是得到操作指令)
2.jvm只有一个堆区(heap)被所有线程共享，堆中不存放基本类型和对象引用，只存放对象本身.
3.一般由程序员分配释放，若程序员不释放，程序结束时可能由OS回收。
栈区:对象实例在Heap 中分配好以后，需要在Stack中保存一个4字节的Heap内存地址，用来定位该对象实例在Heap 中的位置，便于找到该对象实例。
1.每个线程包含一个栈区，栈中只保存基础数据类型的对象和自定义对象的引用(不是对象)，对象都存放在堆区中
2.每个栈中的数据(原始类型和对象引用)都是私有的，其他栈不能访问。
3.栈分为3个部分：基本类型变量区、执行环境上下文、操作指令区(存放操作指令)。
4.由编译器自动分配释放，存放函数的参数值，局部变量的值等．
静态区/方法区:
1.方法区又叫静态区，跟堆一样，被所有的线程共享。方法区包含所有的class和static变量。
2.方法区中包含的都是在整个程序中永远唯一的元素，如class，static变量。
3.全局变量和静态变量的存储是放在一块的，初始化的全局变量和静态变量在一块区域，未初始化的全局变量和未初始化的静态变量在相邻的另一块区域。

附：

堆和栈是程序运行的关键，应该将其理解清楚。

栈是运行时的单位，而堆是存储时的单位。

堆中存的是对象。栈中存的是基本数据类型和堆中对象的引用。一个对象的大小是不可估计的，或者说是可以动态变化的，但是在栈中，一个对象只对应了一个4btye的引用（堆栈分离的好处）。

为什么要把堆和栈区分出来呢？栈中不是也可以存储数据吗？

第一，从软件设计的角度看，栈代表了处理逻辑，而堆代表了数据。这样分开，使得处理逻辑更为清晰。分而治之的思想。这种隔离、模块化的思想在软件设计的方方面面都有体现。
第二，堆与栈的分离，使得堆中的内容可以被多个栈共享（也可以理解为多个线程访问同一个对象）。这种共享的收益是很多的。一方面这种共享提供了一种有效的数据交互方式(如：共享内存)，另一方面，堆中的共享常量和缓存可以被所有栈访问，节省了空间。
第三，栈因为运行时的需要，比如保存系统运行的上下文，需要进行地址段的划分。由于栈只能向上增长，因此就会限制住栈存储内容的能力。而堆不同，堆中的对象是可以根据需要动态增长的，因此栈和堆的拆分，使得动态增长成为可能，相应栈中只需记录堆中的一个地址即可。
第四，面向对象就是堆和栈的完美结合。其实，面向对象方式的程序与以前结构化的程序在执行上没有任何区别。但是，面向对象的引入，使得对待问题的思考方式发生了改变，而更接近于自然方式的思考。当我们把对象拆开，你会发现，对象的属性其实就是数据，存放在堆中；而对象的行为（方法），就是运行逻辑，放在栈中。我们在编写对象的时候，其实即编写了数据结构，也编写的处理数据的逻辑。不得不承认，面向对象的设计，确实很美。

说一说，heap和stack有什么区别。

请你设计一个算法，用来压缩一段URL？

谈一谈，id全局唯一且自增，如何实现？

一个长度为N的整形数组，数组中每个元素的取值范围是[0,n## 1],判断该数组否有重复的数，请说一下你的思路并手写代码

请问求第k大的数的方法以及各自的复杂度是怎样的，另外追问一下，当有相同元素时，还可以使用什么不同的方法求第k大的元素

判断一个链表是否为回文链表，说出你的思路并手写代码

回文链表具有对称性，可以用快慢指针求解。

快指针一次走两步，慢指针一次走一步，快指针指向末尾时，慢指针刚好指向链表中间，也就是前半部分链表的尾节点，返回慢指针，用慢指针获取后半分链表的头节点，并反转。具体如下：

思路

整个流程可以分为以下五个步骤：

找到前半部分链表的尾节点。
反转后半部分链表。
判断是否回文。
恢复链表。
返回结果。

执行步骤一，我们可以计算链表节点的数量，然后遍历链表找到前半部分的尾节点。

我们也可以使用快慢指针在一次遍历中找到：慢指针一次走一步，快指针一次走两步，快慢指针同时出发。当快指针移动到链表的末尾时，慢指针恰好到链表的中间。通过慢指针将链表分为两部分。

若链表有奇数个节点，则中间的节点应该看作是前半部分。

步骤二可以使用「206. 反转链表」问题中的解决方法来反转链表的后半部分。

步骤三比较两个部分的值，当后半部分到达末尾则比较完成，可以忽略计数情况中的中间节点。

步骤四与步骤二使用的函数相同，再反转一次恢复链表本身。

代码

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (head == nullptr) {
            return true;
        }

        // 找到前半部分链表的尾节点并反转后半部分链表
        ListNode* firstHalfEnd = endOfFirstHalf(head);
        ListNode* secondHalfStart = reverseList(firstHalfEnd->next);

        // 判断是否回文
        ListNode* p1 = head;
        ListNode* p2 = secondHalfStart;
        bool result = true;
        while (result && p2 != nullptr) {
            if (p1->val != p2->val) {
                result = false;
            }
            p1 = p1->next;
            p2 = p2->next;
        }        

        // 还原链表并返回结果
        firstHalfEnd->next = reverseList(secondHalfStart);
        //返回结果
        return result;
    }

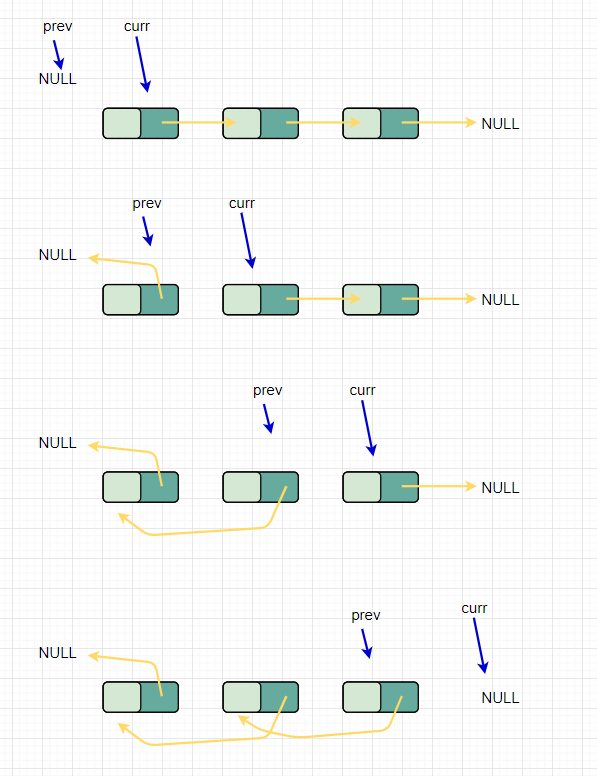
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        while (curr != nullptr) {
            ListNode* nextTemp = curr->next;
            curr->next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }


    ListNode* endOfFirstHalf(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast->next != nullptr && fast->next->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
};

反转单链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
		ListNode* prev = nullptr;
		ListNode* curr = head;
		while (curr) {
			ListNode* next = curr->next;
			curr->next = prev;
			prev = curr;
			curr = next;
		}
        return prev;        
    }
};