看书标记【R语言数据分析与挖掘实战】5
第五章 挖掘模型
5.1 分类预测
回归分析:回归分析是确定预测属性(数值型)与其他变量间相互依赖的定量。关系的最常用的统计学方法。包括线性回归、非线性回归、Logistic回归(因变量有0-1两种取值)、岭回归(自变量间有多重共线性)、主成分回归(自变量间有多重共线性)、偏最小二乘回归等模型。
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter5/示例程序")
# 读入数据
Data <- read.csv("./data/bankloan.csv")[2:701, ]
# 数据命名
colnames(Data) <- c("x1", "x2", "x3", "x4", "x5", "x6", "x7", "x8", "y")
# logistic回归模型
glm <- glm(y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8,
family = binomial(link = logit), data = Data)
summary(glm)
# 逐步寻优法
logit.step <- step(glm, direction = "both")
summary(logit.step)
# 前向选择法
logit.step <- step(glm, direction = "forward")
summary(logit.step)
# 后向选择法
logit.step <- step(glm, direction = "backward")
summary(logit.step)
决策树:它采用自顶向下的递归方式,在决策树的内部结点进行属性值的比较,并根据不同的属性值从该结点向下分支,叶结点是要学习划分的类。
在各个决策点上使用信息熵作为属性额选择标准,C4.5和CART算法是ID3算法的改进,后两种可以还可以描述连续属性。
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter5/示例程序")
# 读入数据
data <- read.csv("./data/sales_data.csv")[, 2:5]
# 数据命名
colnames(data) <- c("x1", "x2", "x3", "result")
# 计算一列数据的信息熵
calculateEntropy <- function(data) {
t <- table(data)
sum <- sum(t)
t <- t[t != 0]
entropy <- -sum(log2(t / sum) * (t / sum))
return(entropy)
}
# 计算两列数据的信息熵
calculateEntropy2 <- function(data) {
var <- table(data[1])
p <- var/sum(var)
varnames <- names(var)
array <- c()
for (name in varnames) {
array <- append(array, calculateEntropy(subset(data, data[1] == name,
select = 2)))
}
return(sum(array * p))
}
buildTree <- function(data) {
if (length(unique(data$result)) == 1) {
cat(data$result[1])
return()
}
if (length(names(data)) == 1) {
cat("...")
return()
}
entropy <- calculateEntropy(data$result)
labels <- names(data)
label <- ""
temp <- Inf
subentropy <- c()
for (i in 1:(length(data) - 1)) {
temp2 <- calculateEntropy2(data[c(i, length(labels))])
if (temp2 < temp) {
temp <- temp2
label <- labels[i]
}
subentropy <- append(subentropy,temp2)
}
cat(label)
cat("[")
nextLabels <- labels[labels != label]
for (value in unlist(unique(data[label]))) {
cat(value,":")
buildTree(subset(data,data[label] == value, select = nextLabels))
cat(";")
}
cat("]")
}
# 构建分类树
buildTree(data)
人工神经网络ANN:一种模仿大脑神经网络结构和功能而建立的信息处理系统,表示神经网络的输入与输出变量之间关系的模型。
BP神经网络、LM神经网络(基于梯度下降法和牛顿法,收敛快)、RBF径向基神经网络(以任意精度逼近任意连续函数,适合分类问题)、FNN神经网络(汇聚了神经网络和模糊系统的优点)、GMDH神经网络(用于预测,其网路结构不固定,在训练过程中不断改变)、ANFIS自适应神经网络(同FNN)。
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter5/示例程序")
# 读入数据
Data <- read.csv("./data/sales_data.csv")[, 2:5]
# 数据命名
library(nnet)
colnames(Data) <- c("x1", "x2", "x3", "y")
# 最终模型
model1 <- nnet(y ~ ., data = Data, size = 6, decay = 5e-4, maxit = 1000)
pred <- predict(model1, Data[, 1:3], type = "class")
(P <- sum(as.numeric(pred == Data$y)) / nrow(Data))
table(Data$y, pred)
prop.table(table(Data$y, pred), 1)
分类与预测算法评价:绝对误差与相对误差、平均绝对误差(避免正负相抵消)、均方误差(还原失真程度,加强了数值大的误差在指标中的作用,从而提高指标灵敏性)、均方根误差(代表了预测值的离散程度)、平均绝对百分误差MAPE、Kappa统计(比较多个观测者对同一事物的观测是否一致)、识别准确度Accuracy、识别精确度、反馈率、ROC曲线(反映分类器效率)、混淆矩阵(描绘样本数据的真实属性与识别结果类型之间的关系)
贝叶斯网络:贝叶斯网络又称信度网络,是Bayes方法的扩展,是目前不确定知识表达和推理领域最有效的理论模型之一。
支持向量机:SVM支持向量机根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷,以获得最好的推广能力。
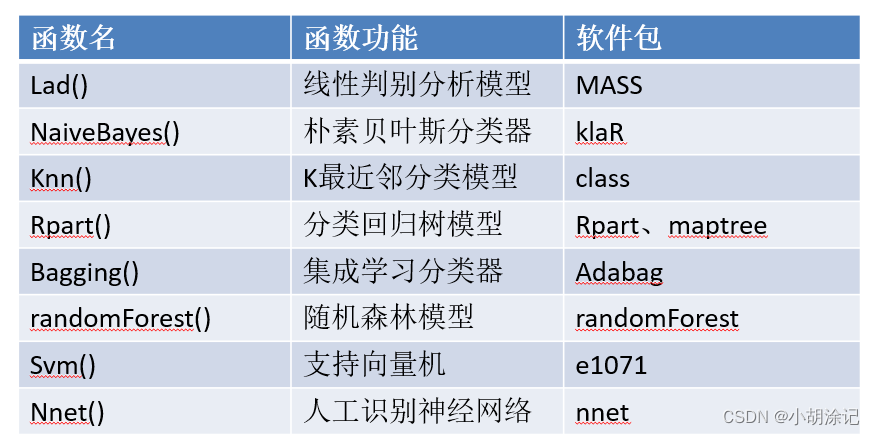
knn对有交叉重叠的待分类样本有较好的判别效果。
5.2 聚类分析
根据数据距离或相似度进行分组的非监督学习算法,划分分组的原则是组内距离最小化而组间距离最大化。
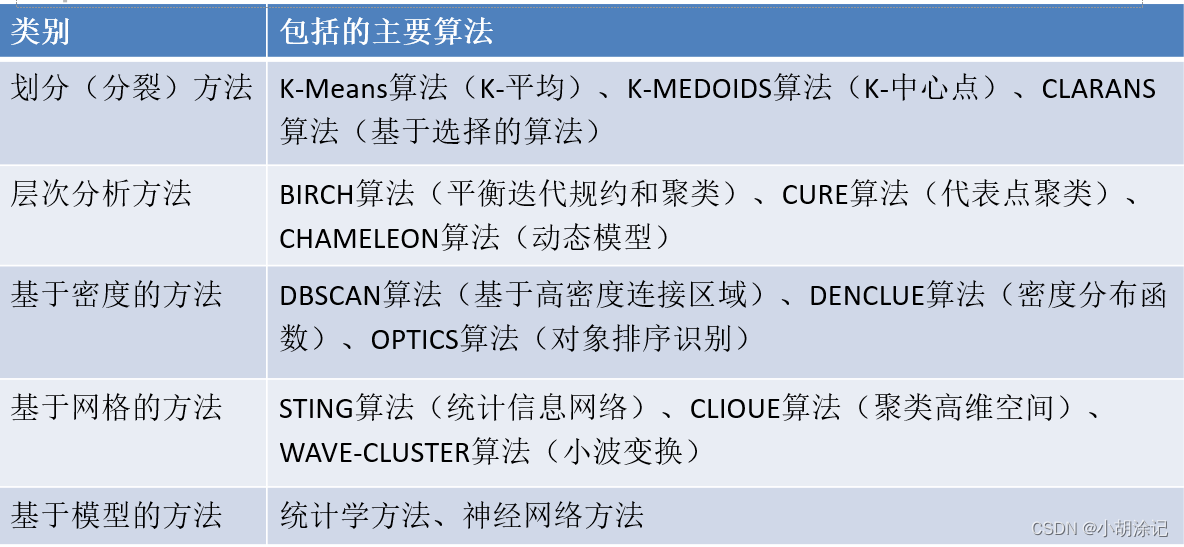
K-means聚类算法过程:
1)从N个样本数据中随机选取K个对象作为初始的聚类中心;
2)分别计算每个样本到各个聚类中心的距离,将对象分配到距离最近的聚类中;
3)所有对象分配完成后,重新计算K个聚类的中心;
4)与前一次计算得到的K个聚类中心比较,如果聚类中心发生变化,转2),否则转5);
5)当质心不发生变化时停止并输出聚类结果。
常规的连续型数据需要对各属性进行零-均值规范化,再度量样本间的距离和样本与簇的距离(用误差平方和SSE作为度量聚类质量的目标函数
S
S
E
=
∑
i
=
1
K
∑
x
∈
E
i
d
i
s
t
(
e
i
,
x
)
2
SSE=\sum_{i=1}^{K}\sum_{x\in E_i}dist(e_i,x)^2
SSE=∑i=1K∑x∈Eidist(ei,x)2)。文档数据时,需要先将文档整理成“文档——词矩阵”,再计算相似度(用余弦相似度度量
S
S
E
=
∑
i
=
1
K
∑
x
∈
E
i
c
o
s
(
e
i
,
x
)
2
SSE=\sum_{i=1}^{K}\sum_{x\in E_i}cos(e_i,x)^2
SSE=∑i=1K∑x∈Eicos(ei,x)2)。
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter5/示例程序")
# 读入数据
Data <- read.csv("./data/consumption_data.csv", header = TRUE)[, 2:4]
km <- kmeans(Data, center = 3)
print(km)
km$size / sum(km$size)
# 数据分组
aaa <- data.frame(Data, km$cluster)
Data1 <- Data[which(aaa$km.cluster == 1), ]
Data2 <- Data[which(aaa$km.cluster == 2), ]
Data3 <- Data[which(aaa$km.cluster == 3), ]
# 客户分群“1”的概率密度函数图
par(mfrow = c(1,3))
plot(density(Data1[, 1]), col = "red", main = "R")
plot(density(Data1[, 2]), col = "red", main = "F")
plot(density(Data1[, 3]), col = "red", main = "M")
# 客户分群“2”的概率密度函数图
par(mfrow = c(1, 3))
plot(density(Data2[, 1]), col="red", main = "R")
plot(density(Data2[, 2]), col="red", main = "F")
plot(density(Data2[, 3]), col="red", main = "M")
# 客户分群“3”的概率密度函数图
par(mfrow = c(1, 3))
plot(density(Data3[, 1]), col="red", main = "R")
plot(density(Data3[, 2]), col="red", main = "F")
plot(density(Data3[, 3]), col="red", main = "M")
聚类分析算法的评价有:purity评价方法(正确的占总数的比例)、RI评价法(用排列组合原理对聚类进行评价的手段,准确率和召回率同样重要)、F值评价法(RI的衍生,对准确率或召回率有一点的偏倚)。
常用的聚类分析算法函数
(1)kmeans(data,centers,iter.max,nstart,algorithm)
data为数据集,centers为预设类别k,iter.max迭代最大值默认为10,nstart为随机起始中心点的次数,algorithm为算法,有Hartigan-Wong、Lloyd、For-gy、MacQueen.
set.seed(2)
x <- matrix(rnorm(50 * 2), ncol = 2)
x[1:25, 1] <- x[1:25, 1] + 3
x[1:25, 2] <- x[1:25, 2] - 4
km.out <- kmeans(x, 2, nstart = 20)
km.out$cluster
plot(x, col = (km.out$cluster + 1), main = "K-Means Clustering Results with K=2", xlab = "", ylab = "", pch = 20, cex = 2)
km.out$centers
points(km.out$centers[1, 1], km.out$centers[1, 2], pch = 10, col = "red", cex = 2)
points(km.out$centers[2, 1], km.out$centers[2, 2], pch = 10, col = "blue", cex = 2)
(2)pam(data,k,metric,…,medoids)
metric用于选择样本点间距离测算的方式,medoids默认取NULL,由软件选择中心点,也可以设定一个k维向量来指定初始点。
(3)dbscan(data,eps,MinPts,scale,method,…)
eps为考察每一样本点是否满足密度要求时,所划定考察领域的半径;MinPts为密度阈值;scale用于选择是否在聚类前先对数据进行标准化,method参数用于选择认定的data类型。
(4)Mclust(data,G,modeNames,…)
G为预设类别数,由BIC值选择最优值;modeNames设定模型类别,由函数自动选取最优值。
5.3 关联规则
关联规则也成为购物篮分析,用于发现两种行为的关联性。
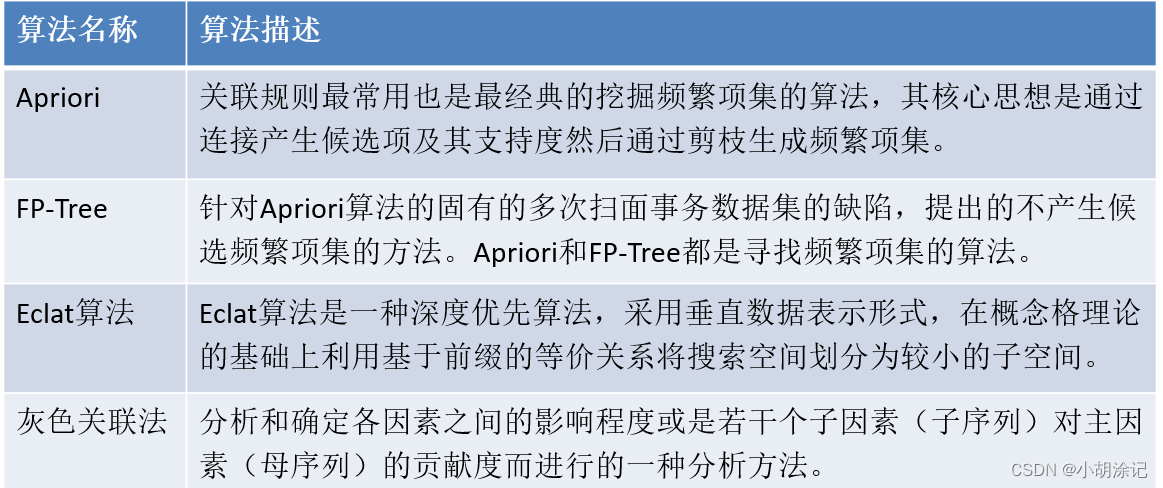
Apriori算法是经典的挖掘频繁项集的算法,通过连接产生候选项与其支持度然后通过剪枝生成频繁项集。支持度
S
u
p
p
o
r
t
(
A
⇒
B
)
=
P
(
A
∪
B
)
Support(A\Rightarrow B)=P(A \cup B)
Support(A⇒B)=P(A∪B),置信度
C
o
n
f
i
d
e
n
c
e
(
A
⇒
B
)
=
P
(
A
∣
B
)
Confidence(A\Rightarrow B)=P(A | B)
Confidence(A⇒B)=P(A∣B),满足规定阈值的规则称为强规则。
# 设置工作空间
install.packages("arules")
library ( arules )
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter5/示例程序")
# 读入数据
tr <- read.transactions("./data/menu_orders.txt", format = "basket", sep=",")
summary(tr)
inspect(tr)
# 支持度0.2,置信度0.5
rules0 <- apriori(tr, parameter = list(support = 0.2, confidence = 0.5))
rules0
inspect(rules0)
用连接-剪枝的方式依据最小支持度阈值(最低重要性)找到所有的频繁项集,然后再用最小置信度阈值(最低可靠性)挖掘得到强关联规则。
5.4 时序模式



定义序列X的自协方差函数
γ
(
t
,
t
)
=
E
[
(
X
t
−
μ
t
)
(
X
s
−
μ
s
)
]
,
γ
(
t
,
t
)
=
γ
(
0
)
=
1
,
ρ
0
=
1
\gamma(t,t)=E[(X_t-\mu_t)(X_s-\mu_s)],\gamma(t,t)=\gamma(0)=1,\rho_0=1
γ(t,t)=E[(Xt−μt)(Xs−μs)],γ(t,t)=γ(0)=1,ρ0=1和自相关系数
ρ
(
t
,
s
)
=
c
o
v
(
X
t
,
X
s
)
σ
t
σ
s
\rho(t,s)=\frac{cov(X_t,X_s)}{\sigma_t\sigma_s}
ρ(t,s)=σtσscov(Xt,Xs),两者衡量的是同一事件在两个不同时期t、s之间的相关程度,过去对未来的影响。
平稳序列:序列在某一常数附件波动且波动范围有限,即存在常数均值和方差,并且延迟k期的序列变量的自协方差和自相关系数是相等的,则称序列为平稳序列。看自相关图或单位根检验(存在单位根就是非平稳序列)都可以。
纯随机性检验:也称白噪声检验,若序列是纯随机的,则
γ
(
k
)
=
0
,
k
≠
0
\gamma(k)=0,k\ne0
γ(k)=0,k=0,常用的检验统计量为Q统计量、LB统计量,由样本延迟阶数可以算得检验统计量,从而得到p值。
自回归移动平均模型(ARMA)是最常用的拟合平稳序列模型,都可以看做是多元线性回归模型。
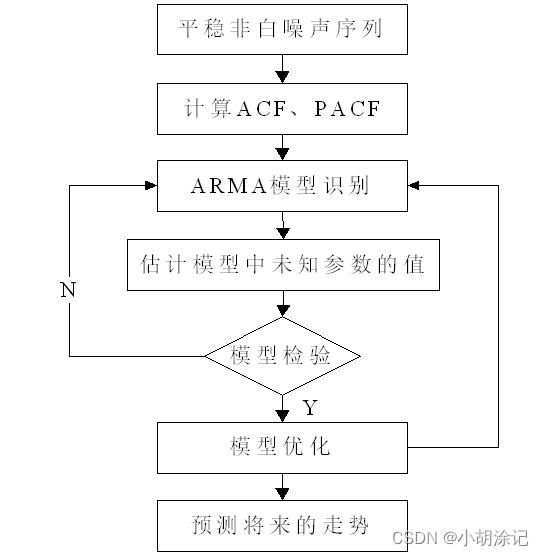
对于平稳序列分析:
自相关系数ACF是用于观察序列X过去对未来的影响,包含了多期X的影响;偏自相关系数PACF仅用于观察X过去某一期t-s对t期的影响,不包含多期X的影响。
AR(p):
x
t
=
ϕ
0
+
ϕ
1
x
t
−
1
+
ϕ
2
x
t
−
2
+
.
.
.
+
ϕ
p
x
t
−
p
+
ε
t
x_t=\phi_0+\phi_1x_{t-1}+\phi_2x_{t-2}+...+\phi_px_{t-p}+\varepsilon_t
xt=ϕ0+ϕ1xt−1+ϕ2xt−2+...+ϕpxt−p+εt,ACF 拖尾,PACF p阶截尾,
E
(
x
t
)
=
μ
=
ϕ
0
1
−
ϕ
1
−
ϕ
2
−
.
.
.
−
ϕ
p
E(x_t)=\mu=\frac{\phi_0}{1-\phi_1-\phi_2-...-\phi_p}
E(xt)=μ=1−ϕ1−ϕ2−...−ϕpϕ0。
MA(p):
x
t
=
μ
+
ε
t
−
θ
1
ε
t
−
1
+
θ
2
ε
t
−
2
+
.
.
.
+
θ
q
ε
t
−
q
x_t=\mu+\varepsilon_t-\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+...+\theta_q \varepsilon_{t-q}
xt=μ+εt−θ1εt−1+θ2εt−2+...+θqεt−q,ACF q阶截尾,PACF拖尾。
ARMA(p,q):
x
t
=
ϕ
0
+
ϕ
1
x
t
−
1
+
ϕ
2
x
t
−
2
+
.
.
.
+
ϕ
p
x
t
−
p
+
ε
t
−
θ
1
ε
t
−
1
+
θ
2
ε
t
−
2
+
.
.
.
+
θ
q
ε
t
−
q
x_t=\phi_0+\phi_1x_{t-1}+\phi_2x_{t-2}+...+\phi_px_{t-p}+\varepsilon_t-\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+...+\theta_q \varepsilon_{t-q}
xt=ϕ0+ϕ1xt−1+ϕ2xt−2+...+ϕpxt−p+εt−θ1εt−1+θ2εt−2+...+θqεt−q.ACF拖尾,PACF拖尾。
p、q的识别有助于模型定阶,然后参数检验、模型检验、模型优化、模型应用预测等。
对于非平稳序列分析:
差分运算:p阶差分(相距一期的两个序列值之间的减法运算称为1阶差分运算);k步差分(相距k期的两个序列值之间的减法运算称为k步差分运算)。
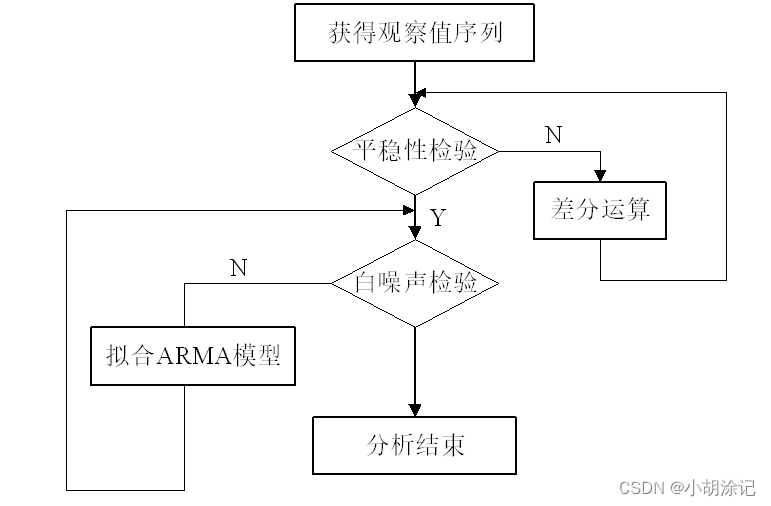
setwd("F:/数据及程序/chapter5/示例程序")
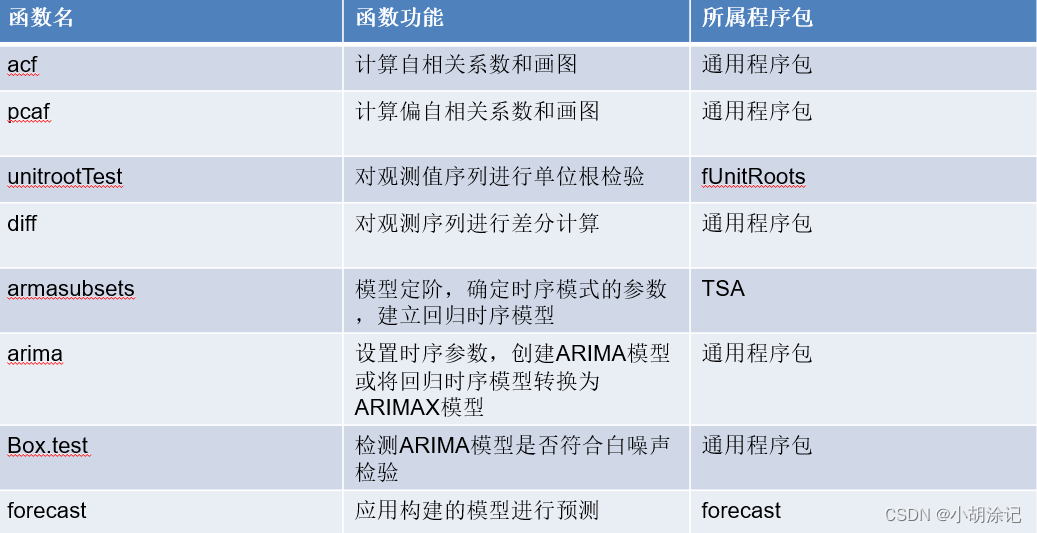
library(forecast)
library(fUnitRoots)
Data <- read.csv("./data/arima_data.csv", header = TRUE)[, 2]
sales <- ts(Data)
plot.ts(sales, xlab = "时间", ylab = "销量 / 元")
# 单位根检验
unitrootTest(sales)
# 自相关图
acf(sales)
# 一阶差分
difsales <- diff(sales)
plot.ts(difsales, xlab = "时间", ylab = "销量残差 / 元")
# 自相关图
acf(difsales)
# 单位根检验
unitrootTest(difsales)
# 白噪声检验
Box.test(difsales, type="Ljung-Box")
# 偏自相关图
pacf(difsales)
# ARIMA(1,1,0)模型
arima <- arima(sales, order = c(1, 1, 0))
arima
forecast <- forecast.Arima(arima, h = 5, level = c(99.5))
forecast
5.5 离群点检测
# 设置工作空间
# 把“数据及程序”文件夹拷贝到F盘下,再用setwd设置工作空间
setwd("F:/数据及程序/chapter5/示例程序")
# 读入数据
Data <- read.csv("./data/consumption_data.csv", header = TRUE)[, 2:4]
Data <- scale(Data)
set.seed(12)
km <- kmeans(Data, center = 3)
print(km)
km$centers
# 各样本欧氏距离
x1 <- matrix(km$centers[1, ], nrow = 940, ncol =3 , byrow = T)
juli1 <- sqrt(rowSums((Data - x1) ^ 2))
x2 <- matrix(km$centers[2, ], nrow = 940, ncol =3 , byrow = T)
juli2 <- sqrt(rowSums((Data - x2) ^ 2))
x3 <- matrix(km$centers[3, ], nrow = 940, ncol =3 , byrow = T)
juli3 <- sqrt(rowSums((Data - x3) ^ 2))
dist <- data.frame(juli1, juli2, juli3)
# 欧氏距离最小值
y <- apply(dist, 1, min)
plot(1:940, y, xlim = c(0, 940), xlab = "样本点", ylab = "欧氏距离")
points(which(y > 2.5), y[which(y > 2.5)], pch = 19, col = "red")