Top100 数组
1.53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
输入:nums = [1] 输出:1示例 3:
输入:nums = [5,4,-1,7,8] 输出:23提示:
1 <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4进阶:如果你已经实现复杂度为
O(n)的解法,尝试使用更为精妙的 分治法 求解。
思路:
1)按照前缀和,进行遍历,代码如下,超时,不可以了,而且时间复杂度有点高,需要优化!
2)
代码:
class Solution(object):
def maxSubArray(self, nums):
sum_s=[nums[0]]
max_s=nums[0]
for i in range(1,len(nums)):
sum_s.append(sum_s[i-1]+nums[i])#前缀和
max_s=max(max_s,sum_s[i-1]+nums[i])
for j in range(0,i):
max_s=max(sum_s[i]-sum_s[j],max_s)
return max_s超时!没必要保存,也没必要内存循环去计算,因为只需要求值,改进如下:
class Solution(object):
def maxSubArray(self, nums):
pre=0
max_s=nums[0]
for i in nums:
pre=max(pre+i,i)
max_s=max(max_s,pre)
return max_sjava:
public class Solution {
public int maxSubArray(int[] nums) {
int pre = 0;
int res = nums[0];
for (int num : nums) {
pre = Math.max(pre + num, num);
res = Math.max(res, pre);
}
return res;
}
}
鸣谢:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
2.56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。提示:
1 <= intervals.length <= 10^4intervals[i].length == 20 <= starti <= endi <= 10^4
思路:
1)暴力:创建一个哈希表,以自然数为序,值为1做标记,代表该元素属于区间内;先扫描intervals数组,每个子列表从starti到endi依次进行判断标记,未出现过则置1,期间要记录一下最大endi(这是下一步扫描的结束点);执行结束后扫描哈希表,并设置一flag,创建空的工作列表:当flag为flase且出现1时,将位置序i加入新列表中两次,并将flag置为true;当出现1但flag为true时,将末尾元素删除加入新的位置序(或置换);当出现0时,flag置为flase,且将已有列表加入res结果数组,并将工作列表清空。
2)官解思想——排序:
如果我们按照区间的左端点排序,那么在排完序的列表中,可以合并的区间一定是连续的。如下图所示,标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间,它们在排完序的列表中是连续的:
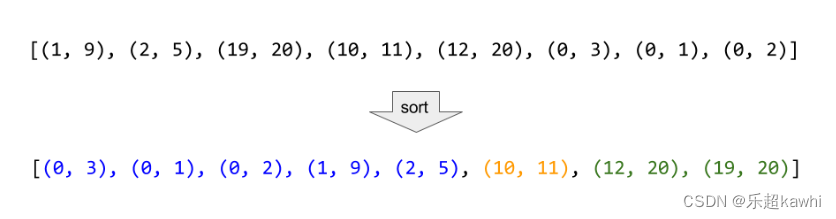
我们用数组 merged 存储最终的答案。首先,我们将列表中的区间按照左端点升序排序。然后我们将第一个区间加入 merged 数组中,并按顺序依次考虑之后的每个区间:
- 如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后,那么它们不会重合,我们可以直接将这个区间加入数组 merged 的末尾;
- 否则,它们重合,我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点,将其置为二者的较大值。
代码:
python
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
#先按照starti进行排序
intervals.sort(key=lambda x: x[0])
merged = []
for interval in intervals:
# 如果列表为空,或者当前区间与上一区间不重合,直接添加
if not merged or merged[-1][1] < interval[0]:
merged.append(interval)
else:
# 否则的话,我们就可以与上一区间进行合并
merged[-1][1] = max(merged[-1][1], interval[1])
return merged
3.189. 轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]提示:
1 <= nums.length <= 10^5-2^31 <= nums[i] <= 2^31 - 10 <= k <= 10^5
思路:
1.笨办法,用空间换时间,用辅助数组来存。
2.本题是右旋转,其实就是反转的顺序改动一下,优先反转整个字符串,步骤如下:
- 反转整个字符串
- 反转区间为前k的子串
- 反转区间为k到末尾的子串
代码:
class Solution(object):
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: None Do not return anything, modify nums in-place instead.
"""
new=[]
n=len(nums)
for i in range(k%n,0,-1):
new.append(nums[-i])
for i in range(n-k%n):
new.append(nums[i])
print(new)
for i in range(n):
nums[i]=new[i]
会超时,优化一下!
我直接求助卡哥:(来自代码随想录python)
class Solution:
def rotate(self, A: List[int], k: int) -> None:
def reverse(i, j):
while i < j:
A[i], A[j] = A[j], A[i]
i += 1
j -= 1
n = len(A)
k %= n
reverse(0, n - 1)
reverse(0, k - 1)
reverse(k, n - 1)
4.238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums =[1,2,3,4]输出:[24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]提示:
2 <= nums.length <= 10^5-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内进阶:你可以在
O(1)的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
思路:
1.哈哈哈哈哈,我一眼克拉默法则求根,求出所有积,各自除哈哈哈!(开玩笑的,这个不允许)
2.不能使用除法,那就是考虑两边向中间计算,用两次遍历,分别计算前缀积?(也就是求某一个元素的的前缀积?和后缀积?),然后把该位置上的前缀X后缀,就可以得到了
时间复杂度O(n)
代码:
class Solution(object):
def productExceptSelf(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
n=len(nums)
pre=[nums[0]]
post=[nums[n-1]]
for i in range(1,n):
pre.append(pre[i-1]*nums[i])
post.append(post[i-1]*nums[n-1-i])#虽然从前往后,但用的时候从后往前
result=[post[n-2]]
print(result)
for i in range(1,n):
result.append(pre[i-1]*post[n-2-i])
# print(result)
result[n-1]=pre[n-2]
return result里面有些细节需要扣一扣,在考虑边界的问题上需要特别注意!!(不过还是一遍遍debug最后得到结果,来得最踏实)
5.41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0] 输出:3示例 2:
输入:nums = [3,4,-1,1] 输出:2示例 3:
输入:nums = [7,8,9,11,12] 输出:1提示:
1 <= nums.length <= 5 * 10^5-2^31 <= nums[i] <= 2^31 - 1
思路:
代码:
class Solution(object):
def firstMissingPositive(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
nums.sort()
xxx=nums[-1]
if xxx < 0 or nums[0] > 1 :
return 1
else:
temp=nums[0]+1
while temp <= xxx+1 :
if temp not in nums and temp > 0:
return temp
else:
temp+=1超时了,哭死!看个大佬的java题解吧!学!好好学!
import java.util.HashSet;
import java.util.Set;
public class Solution {
public int firstMissingPositive(int[] nums) {
int len = nums.length;
Set<Integer> hashSet = new HashSet<>();
for (int num : nums) {
hashSet.add(num);
}
for (int i = 1; i <= len ; i++) {
if (!hashSet.contains(i)){
return i;
}
}
return len + 1;
}
}