【二叉树搜索树/二叉排序树】BST树的创建,插入,找最小结点的下一个节点/找最大结点的前驱
基本概念:
二叉树搜索树:【二叉排序树】
- 每个结点都有一个作为搜索一句的关键码,所有的结点的关键码给互不相同
- 左子树(如果存在)所有结点的关键码都小于根结点的关键码
- 右子树(如果存在)所有结点的关键码都大于根节点的关键码
- 左子树和右子树也都是二叉搜索树。
特点:说人话,大的放右边,小的放左边。
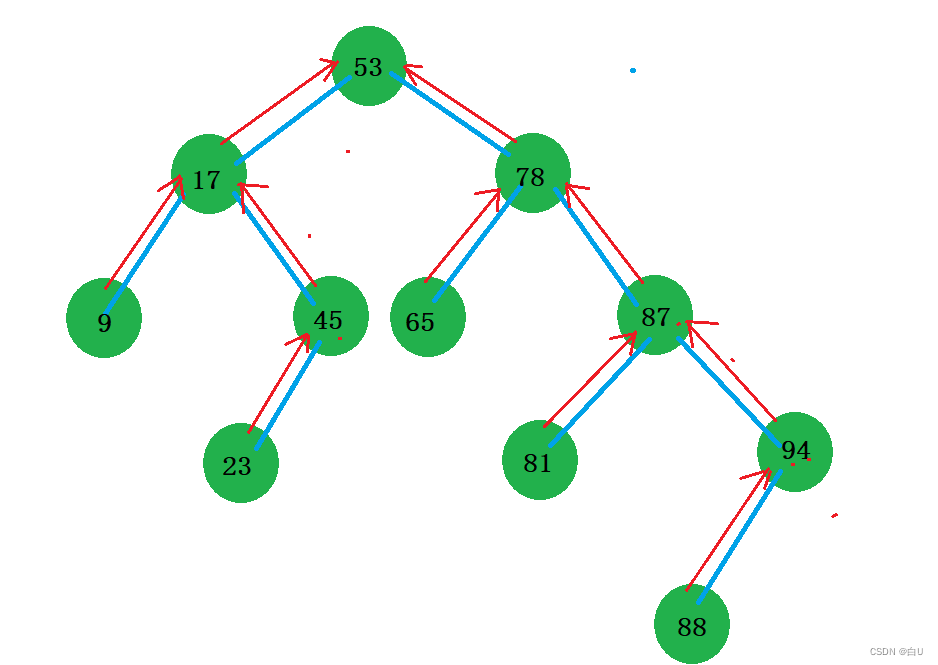
如果对一颗二叉排序树进行中序遍历,就可以按照从小到大的顺序,将各个结点的关键码排列。
创建一棵二叉排序树
有三个指向: parent ,leftchild,rightchild
二叉搜索树结构设计:
typedef int KeyType;
typedef struct {
struct BstNode* parent;
struct BstNode* leftchild;
struct BstNode* rightchild;
KeyType* key;
}BstNode;
typedef struct
{
BstNode*root;
int cursize;
}BSTree;
查询函数:
BstNode FindValue(BSTree *tree,int kx)
{
BStree *ptr = tree->root;
while( ptr!= nullptr || ptr->key != kx)
{
ptr = ptr->key < kx ? ptr->leftchild:ptr->rightchild;
}
return ptr;
}
BstNode *Search(BstNode*ptr,KeyType kx)
{
if(ptr == nullptr || ptr->key == kx) return ptr;
else if(kx > ptr->key) { return Search(ptr->rightchild,kx);}
else {return Search(ptr ->leftchild,kx);}
}
BstNode *SearchValue(BSTree *ptree,KeyType kx)
{
return Search(ptree->root ,KeyType kx)
}
插入思想:
- 先插入根结点。
- 插入后,开始判断根节点是否为空以及待插入的数是否等于当前结点的数,如果不等于空,则保存根节点,并判断kx的值小于还是大于key
- 如果大于,走右边,小于走左边,再次判断如果满足当前结点不为空,是否和当前结点的key值相等,相同返回false
- 否则为空,申请结点,存入kx,并将双亲结点指向它的根结点
- 判断,小于根的左孩子指向它,大于右孩子指向它。
**加个引用就可以改变root int p = &a; int &s = p; 作为s指针p的别名
bool Insert(BstNode *&ptr, KeyType kx)
{
/*if (ptr == NULL) //先判定 ptr是否为空,如果为空
{
ptr = MakeRoot(kx);//创建一个根节点,这里的ptr赋值,并不能给root赋值
return true; //加个引用就可以了。
}*/
//否则
BstNode* pa = NULL;
BstNode* p = ptr;
================== 要插入的值和树中的的值相同
while (p != NULL && p->key != kx)
{
pa = p; //用来保存双亲结点
if (kx < pa->key) p = pa->leftNode;
else p = pa->rightNode;
}
//现在p的指向为空或者要插入的值和树中的的值相同,直接退出
if (p != NULL && p->key == kx) return false;
================== 如果p为空,或者kx值在树中不存在
p = BuyNode();
p->key = kx;
p->parent = pa;
==================== 如果为空没有根节点。则走下面
if (ptr == NULL) //先判定 ptr是否为空,如果为空
{ //p成为根节点
ptr = p;//创建一个根节点,这里的ptr赋值,并不能给root赋值
//加个引用就可以了。
}
else
{
if (p->key < pa->key)pa->leftNode = p;
else pa->rightNode = p;
return true;
}
}
void InOrder(BstNode *ptr)
{
if (ptr != nullptr)
{
InOrder(ptr->leftNode);
cout << ptr->key << " ";
InOrder(ptr->rightNode);
}
}
找到二叉排序树的最左边结点,则是最小的**
BstNode* First(BstNode* ptr)
{
while (ptr != NULL && ptr->leftNode != NULL)
{
ptr = ptr->leftNode;
}
return ptr;
}
找最小结点的下一个节点。**
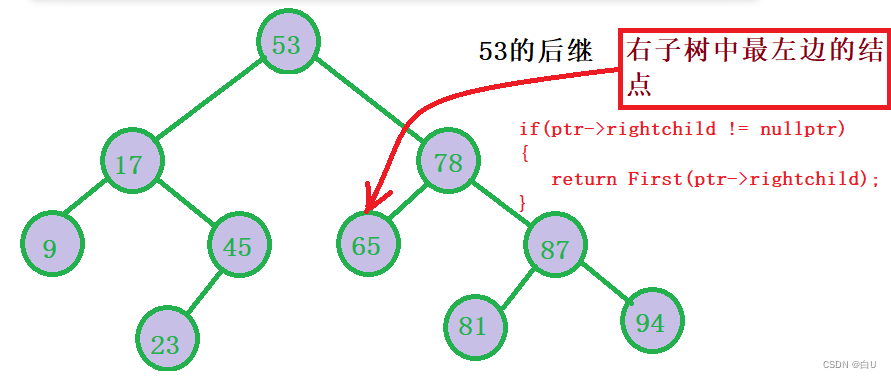
BstNode* Next(BstNode* ptr)
{
if (ptr == NULL) return NULL;
if (ptr->rightNode != NULL)
{
return First(ptr->rightNode);//找到最左边的数
}
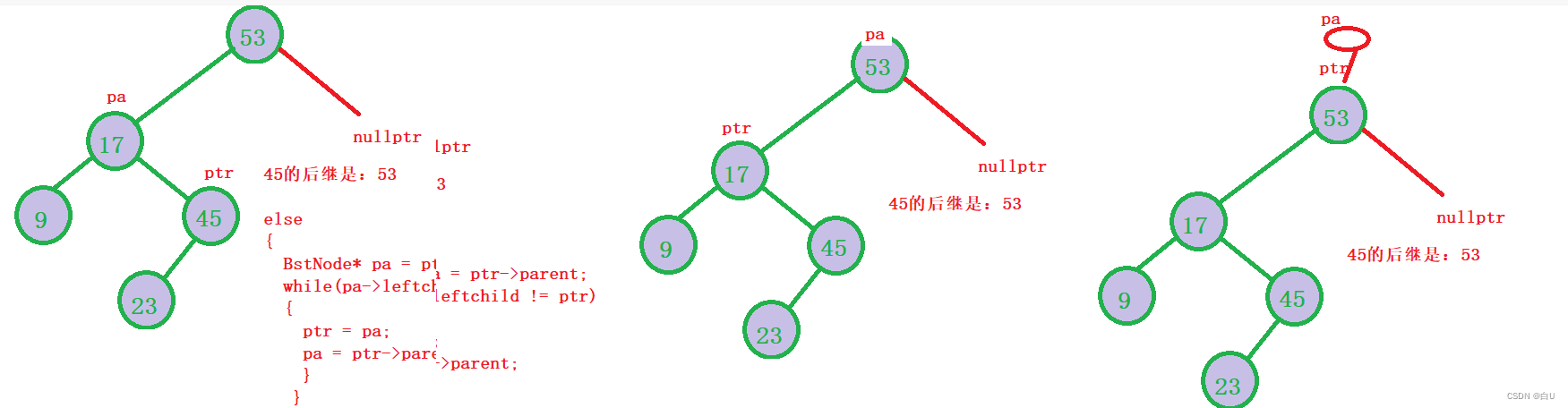
else
{ //核心代码
BstNode* pa = ptr->parent;
while (pa != NULL && pa->leftNode != ptr)
{
ptr = pa;
pa = ptr->parent;
}
return pa; //中序遍历的最左边结点的后继
}
}
//
void NiceOreder(BstNode* ptr)
{
for (BstNode* p = First(ptr); p != NULL; p = Next(p))
{
cout << p->key << " ";
}
cout << endl;
}
找最后一个结点
//找最后一个节点
BstNode* last(BstNode* ptr)
{
while (ptr != NULL && ptr->rightNode != NULL)
{
ptr = ptr->rightNode;
}
return ptr;
}
找前驱
//找前驱
BstNode* Pre(BstNode* ptr)
{
if (ptr == NULL) return NULL;
if (ptr->leftNode != NULL)
{
return last(ptr->leftNode);//找到最左边的数
}
else
{
BstNode* pa = ptr->parent;
while (pa != NULL && pa->rightNode != ptr)
{
ptr = pa;
pa = ptr->parent;
}
return pa; //中序遍历的最左边结点的后继
}
}
//倒叙
void RevNiceOreder(BstNode* ptr)
{
for (BstNode* p = last(ptr); p != NULL; p = Pre(p))
{
cout << p->key << " ";
}
cout << endl;
}
int main()
{
BSTree root = NULL;
int ar[] = { 53,17,78,9,45,65,87,23,81,94,88,100 };
int n = sizeof(ar) / sizeof(ar[0]);
for (int i = 0; i < n; ++i)
{
cout << Insert(root, ar[i]) << endl;;
}
InOrder(root);
cout << endl;
}