【运筹优化】运筹学导论:求解线性规划问题 - 单纯形法
在阅读本博客前,请了解线性规划相关的知识:【运筹优化】运筹学导论:线性规划导论
单纯形法是求解线性规划问题的基本方法,它是由 George Dantzig 于 1947 年提出的。单纯形法已经被证明是真正有效的方法,如今通常用于在计算机上解决大型问题。
本博客介绍单纯形法的主要内容,介绍它的一般原理、几何解释以及如何用它求解任意标准形式的线性规划问题。
一、单纯形法的实质(几何原理)
单纯形法是一个代数计算过程,它本质上是基于几何原理。为了说明单纯形法的一般几何原理,将以 【运筹优化】运筹学导论:线性规划导论 中提到的 Wyndor Glass 公司问题为例。
该例子的模型和图形如下图所示。其中,每个约束边界是一条直线,约束边界的交点是这个问题的角点解(corner-point solution),在可行域上的角点解被称为角点可行解(CPF solution)
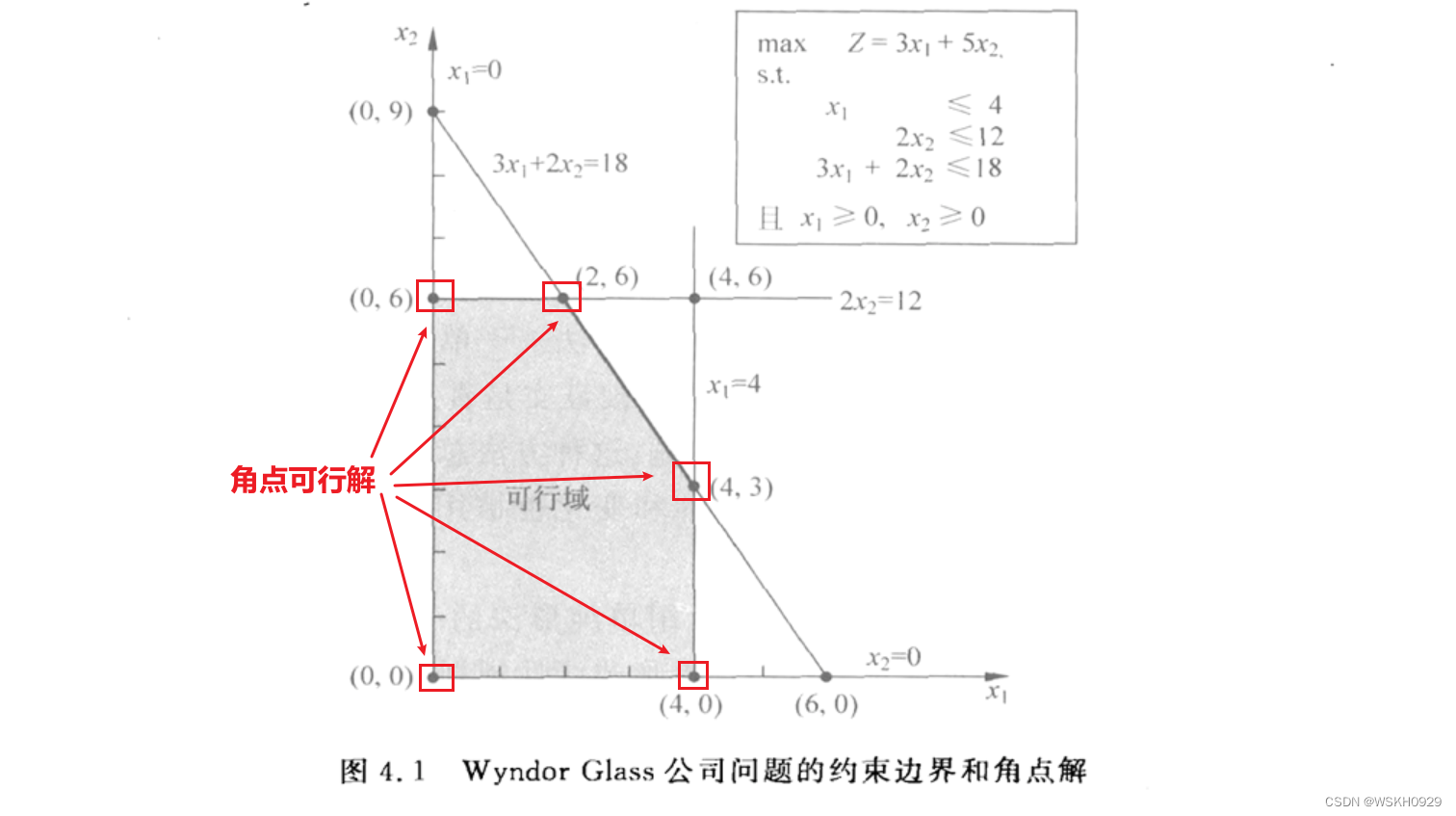
定理:对于一个有 n 个决策变量的线性规划问题来说,每个角点解位于 n 条约束边界的交点处(在 Wyndor Glass 公司的例子中,仅有 2 个决策变量,因此,每个角点解位于 2 个约束边界线的交点处)
根据上述定理,我们可以推广得到:
定理:对于任意含有 n 个决策变量的线性规划问题,当 2 个 CPF 解位于 n-1 条相同的约束边界上时,则它们是相邻的。这两个相邻的 CPF 解连成一条线段,这个线段在约束边界上,被称为可行域的边(edge)。
在 Wyndor Glass 公司的例子中,2 条约束边界产生一个 CPF 解,因此,每个 CPF 解都有两个相邻的 CPF 解(每个都在两条边之一的另一端,正如表 4.1 所列举的那样)。

我们之所以对相邻的 CPF 解感兴趣,是因为后续介绍的这些解的基本性质能够为我们判断某个 CPF 解是否最优提供有效的思路。

例如,根据表 4.1 ,由于 CPF 解(2,6)的 Z=36,大于 (0,6) 对应的 Z=30 和 (4,3) 对应的 Z=27,因此,它必定是最优的。
最优性检验是单纯形法的一个步骤,在判断是否得到最优解时使用。
1.1 示例的求解


1.2 关键的解原理
这一节介绍单纯形法六个关键的解原理,这些解原理提供了前一小节所述步骤背后的基本原理
1.2.1 解原理1
第一个解原理给出了线性规划问题中 CPF 解和最优解之间的关系。
解原理1:对于至少有一个最优解的线性规划问题来说,最好的 CPF 解一定是最优解。因此,单纯形法只关注 CPF 解。
在线性规划问题中,可行解一般有无限多个,运用解原理1可以将需要测试的解的个数缩减到一个很小的有限的数,这是一个大大的简化。
1.2.2 解原理2
第二个解原理定义单纯形法的过程
解原理2:单纯形法是一个迭代算法,它重复着一系列固定的步骤,直到得到最优解。
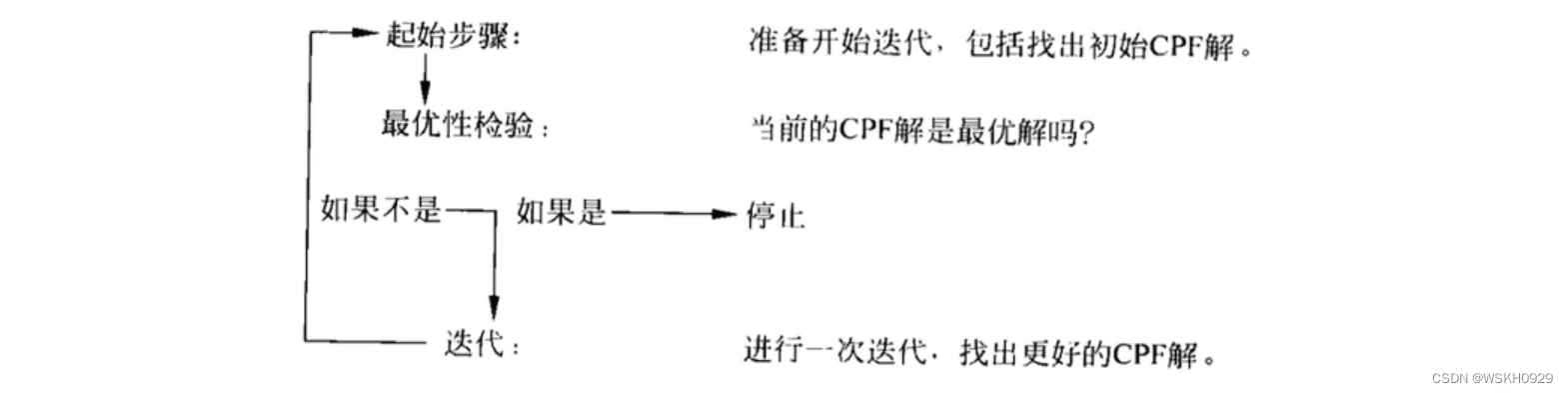
单纯形法迭代步骤如下:
1.2.3 解原理3
解原理3定义了单纯形法的一般起始步骤
解原理3:只要有可能,单纯形法的起始步骤就选择原点(所有决策变量为0)作为初始的 CPF 解。
如果所有决策变量均为非负的话,一般选择原点作为初始 CPF 解是可能的,因为这些非负约束的边界相交形成的原点就是角点解,除非它因不满足一个或多个约束条件而不可行。
当有太多决策变量以致于不能用图解的方式找出初始 CPF 解时,应用解原理3可以减少为寻找初始 CPF 解而需要使用的代数运算步骤。
1.2.4 解原理4
解原理4:已知一个 CPF 解,从计算上来说,获取它的相邻 CPF 解的信息比获取其他 CPF 解的信息快。
根据解原理4,单纯形法迭代时,从当前 CPF 解移向更好的 CPF 解的计算总是考虑相邻的 CPF 解,不考虑其他的 CPF 解。因此,后续直至寻找出最优解的全部轨迹实际上是沿着可行域的边界的。
1.2.5 解原理5
解原理5:得到当前的 CPF 解后,单纯形法考察从这个解出发的可行域的每一条边。虽然每一条边都指向另一端的相邻 CPF 解,但是单纯形法不需要计算相邻 CPF 解,而是仅仅判断沿着这条边移动时 Z 的增长率。在拥有正的增长率的边界线中,单纯形法总是选择增长率最大的边移动。当求出这条边另一端的相邻 CPF 解后,它就会作为新的当前的 CPF 解,进行下一次最优性检验和迭代。

1.2.6 解原理6
解原理6实际上是解原理5的推广
解原理6:最优性检验就是检查是否存在一条边从当前 CPF 解出发,带给 Z 正的增长率,如果没有,则证明当前 CPF 解是最优解。

二、构建单纯形法(代数原理)
前面介绍了单纯形法的几何原理,但是这个算法通常是在计算机上实施的,计算机只能执行代数运算,因此需要把上述几何原理描述的求解过程转化为可应用的代数计算步骤。
代数求解步骤是建立在求解方程组的基础上的,因此,构建单纯形法代数运算的第一步是把不等式约束转化为等式约束。这个转化依靠引入松弛变量 (slack variables) 完成。
为了说明这个转化过程,还是以 Wyndor Glass 公司问题为例:

关于松弛变量的额外解释如下:
- 如果当前解中的某个松弛变量等于0,则该解位于对应约束条件的约束边界线上
- 如果当前解中的某个松弛变量小于0,则该解在约束条件边界不可行的一侧
- 如果当前解中的某个松弛变量大于0,则该解在约束条件边界可行的一侧
之前介绍的术语(如 CPF 解)仅仅适用于问题的原始形式,因此我们仍然需要介绍与扩展形式相对应的术语
扩展解(augmented solution):是原始变量(决策变量)取值再加上松弛变量取值后形成的解。
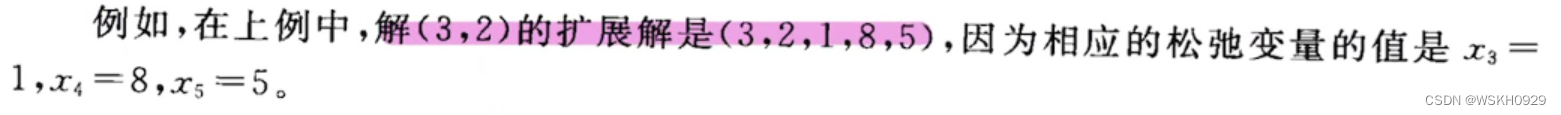
基本解(basic solution):是扩展后的角点解。

基本可行解(BF 解):是扩展的 CPF 解。

基本解和角点解(或者 BF 解和 CPF 解)的唯一区别在于是否包含松弛变量。
因为基本解和 BF 解是线性规划标准词汇中非常重要的部分,因此我们需要弄清楚它们的代数性质。
在 Wyndor Glass 公司的例子中,注意到约束方程组中有 5 个变量和 3 个等式,因此有:

一个基本解有如下性质:
- 每个变量都可以作为非基变量或基变量
- 非基变量(non-basic variables) 的值设为0
- 基变量(basic variables) 的值作为方程组(约束条件的扩展形式)的联立解被求得,这一组基变量通常被称为 “基”
- 基变量的个数等于约束条件(方程)的个数。因此,非基变量的个数等于变量总数减去约束条件个数
- 如果基变量满足非负约束,则基本解为 BF 解

就像称两个 CPF 解是相邻的一样,与之对应的 BF 解也被称作是相邻的。
这里有一个判断 2 个 BF 解是否相邻的简单方法: 当非基变量只有一个不同时,两个 BF 解相邻。这意味着,基变量除了一个不同外其余也是相同的,虽然其数值可能不同。
因此,从当前 BF 解移动到另一个相邻的 BF 解时,通常围绕着把一个变量从非基变量转变为基变量来进行。

当我们处理问题的扩展形式时,同时把目标函数当作新的约束方程考虑和处理会很方便。因此,在我们开始单纯形法前,这个问题需要用同样的方法再改写一下:

三、单纯形法的代数形式
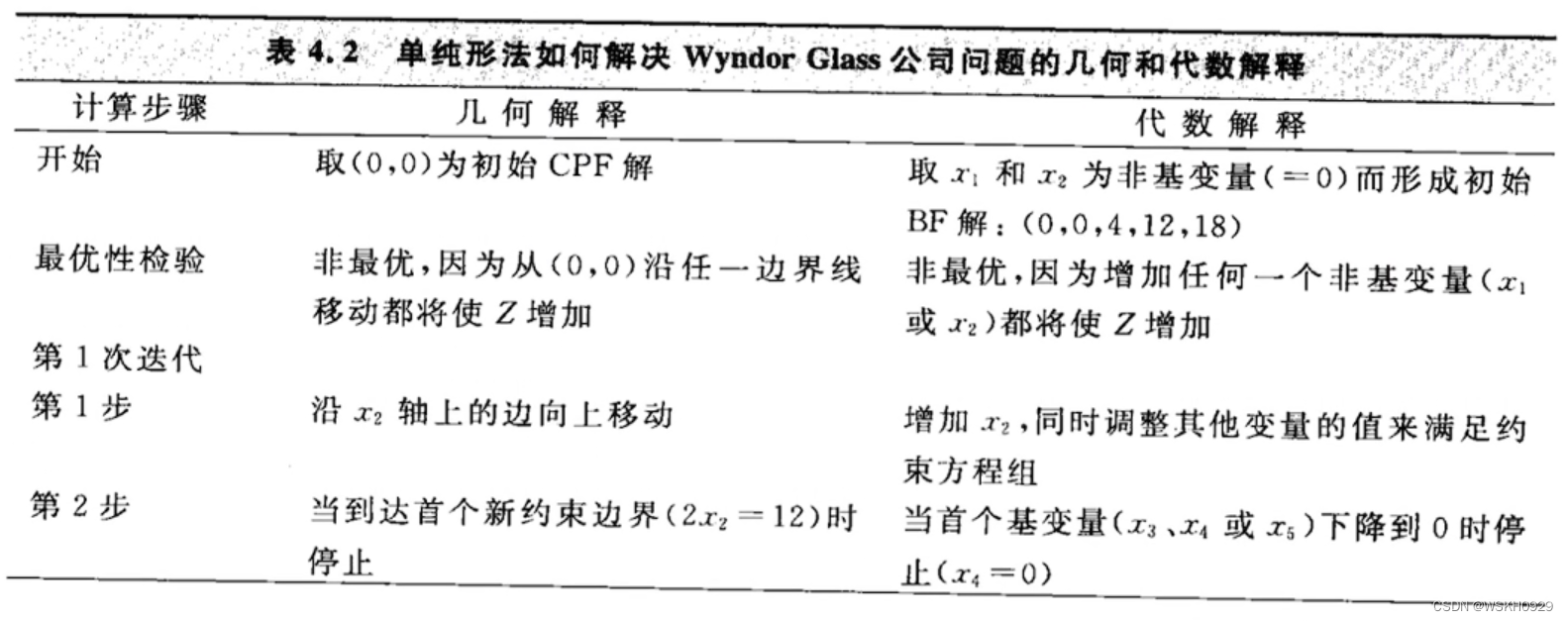
为了把单纯形法的几何原理和代数原理联系起来,在表 4.2 中,从几何和代数两个角度概述了单纯形法是如何求解 Wyndor Glass 公司案例的。

3.1 初始化

3.2 最优性检验


3.3 确定移动的方向(迭代的步骤1)


3.4 确定在何处停下(迭代的步骤2)


3.5 求解新的BF解(迭代的步骤3)



3.6 新BF解的最优性检验

3.7 第2次迭代和最优解结果


四、单纯形法的表格形式
上一节讲述的单纯形法的代数形式可能是理解该算法基本逻辑关系最好的计算形式,然而,它不是进行所需计算的最简便的形式。当你需要手工解决问题时,推荐采用这节中讲述的表格形式。
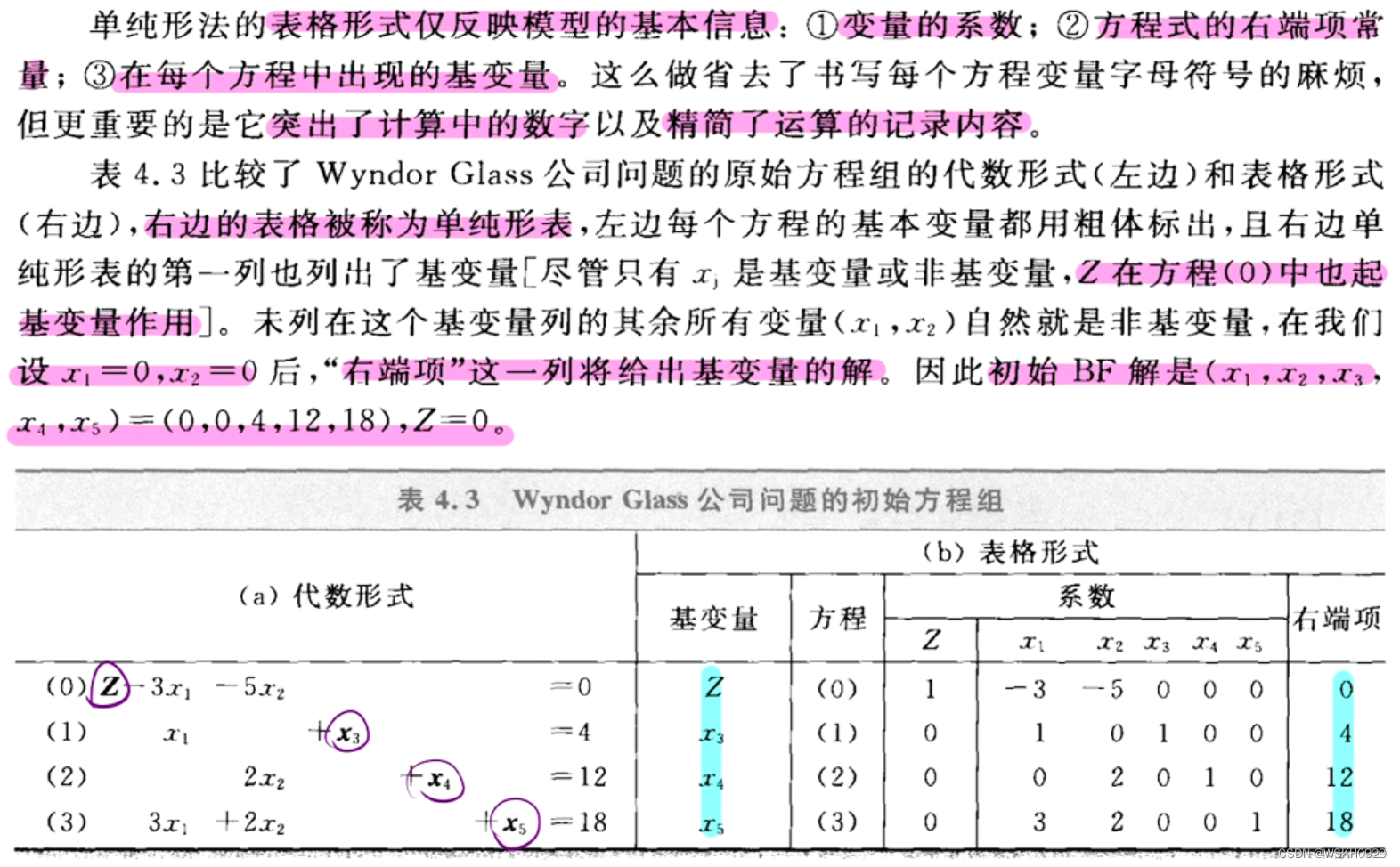
4.1 单纯形法的总结(以迭代1为例)
这一节,总结单纯形法的表格形式,同时简单地介绍它在 Wyndor Glass 公司问题中的应用。记住,这个逻辑与上一节讲述的代数形式是一样的。只是当前和后续迭代得到的方程组的表现形式有了改变。还有,在最优性检验或进行迭代中步骤1和步骤2做判断时,我们无需把变量移动到方程的右端项。
4.1.1 初始化

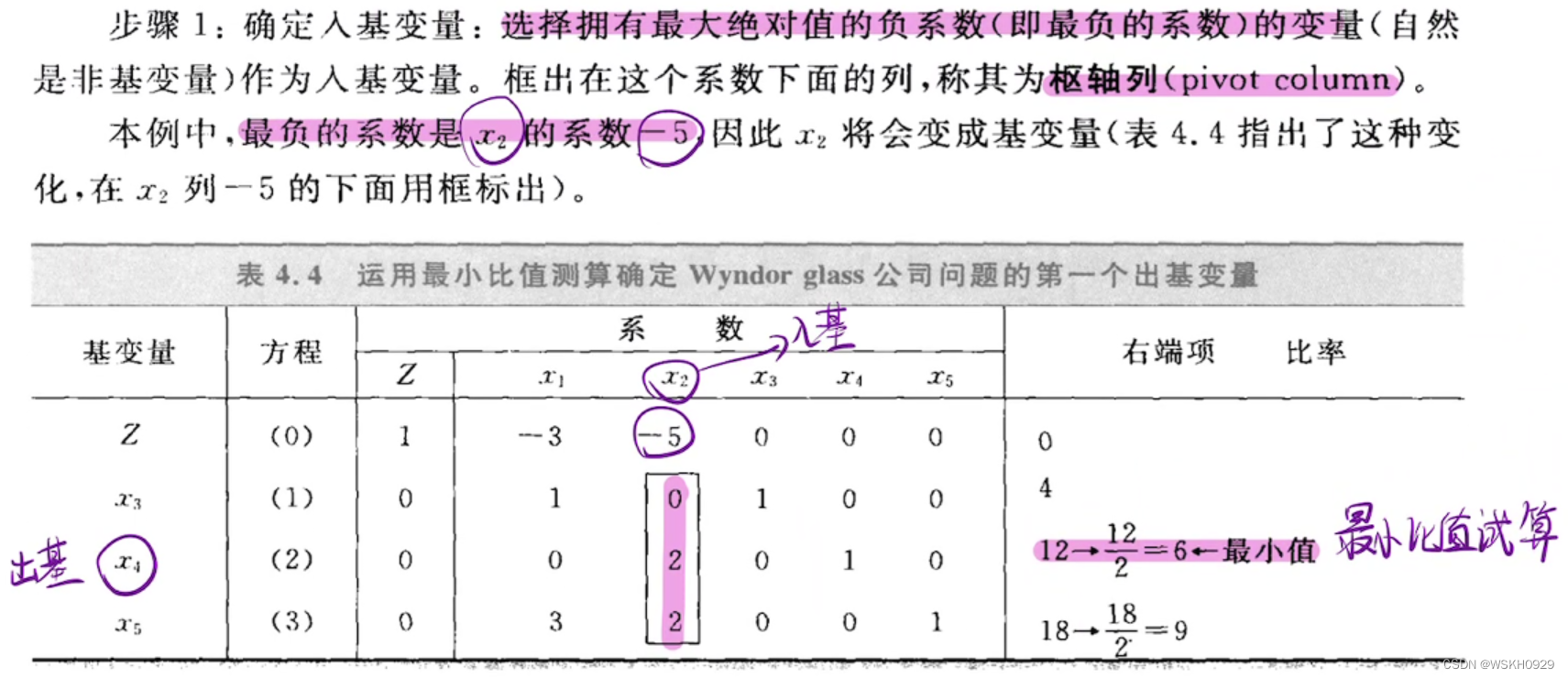
4.1.2 最优性检验

4.1.3 迭代

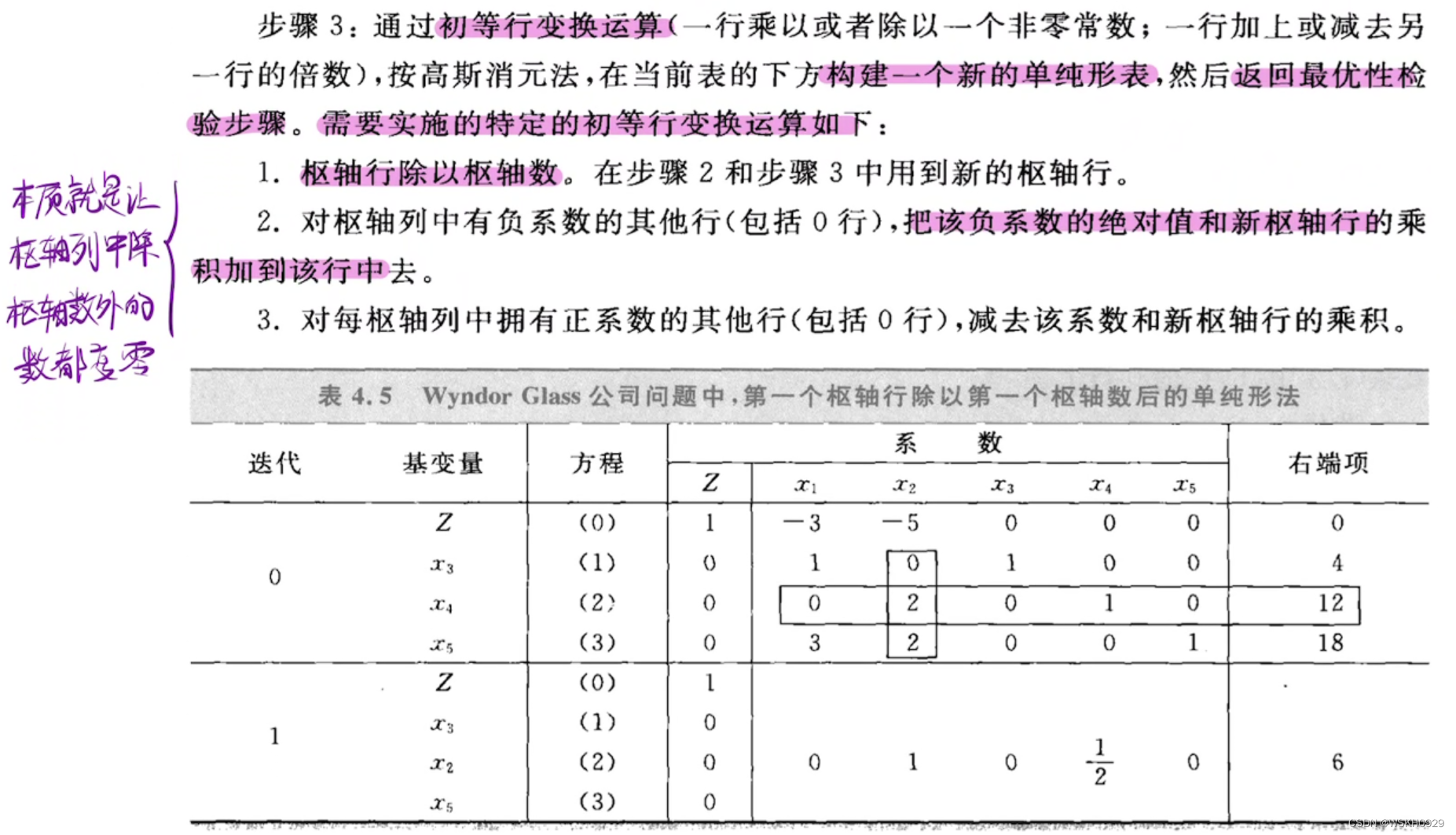

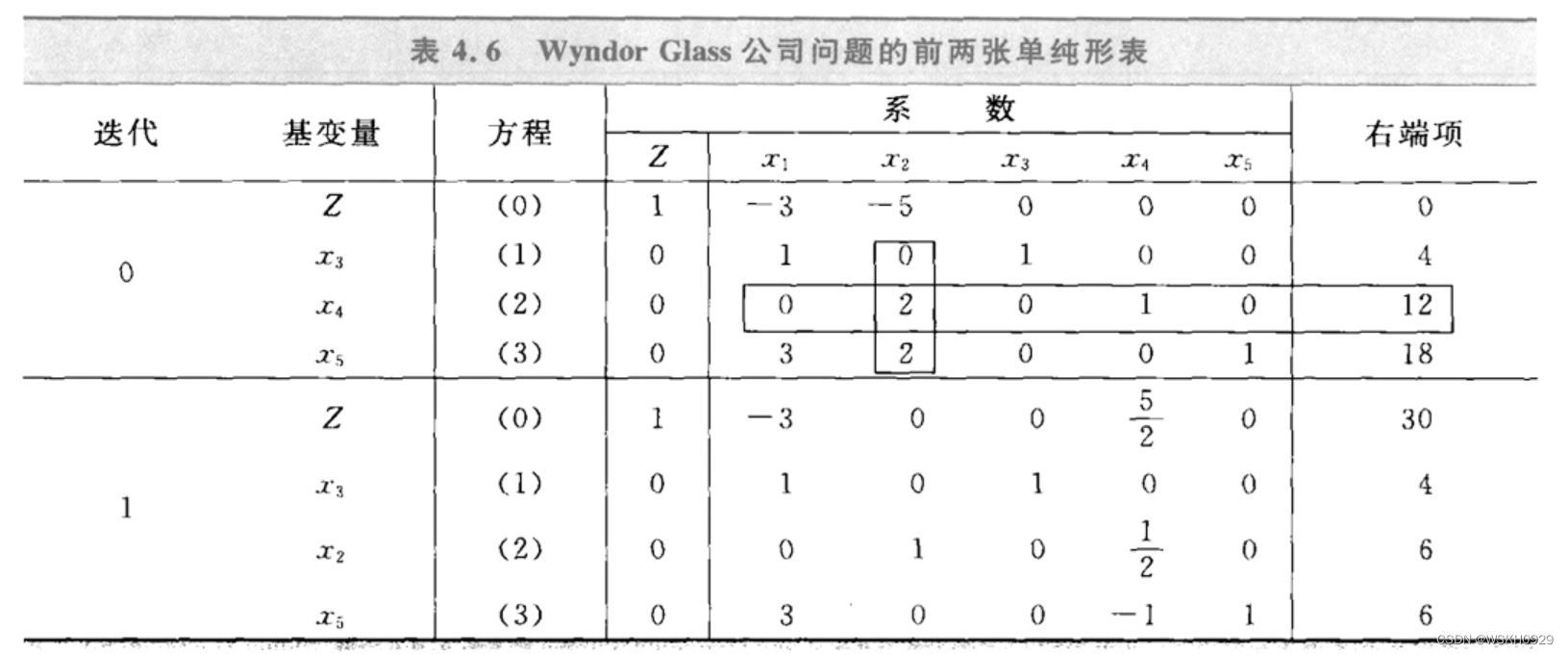
4.1.4 第二次迭代与最优解
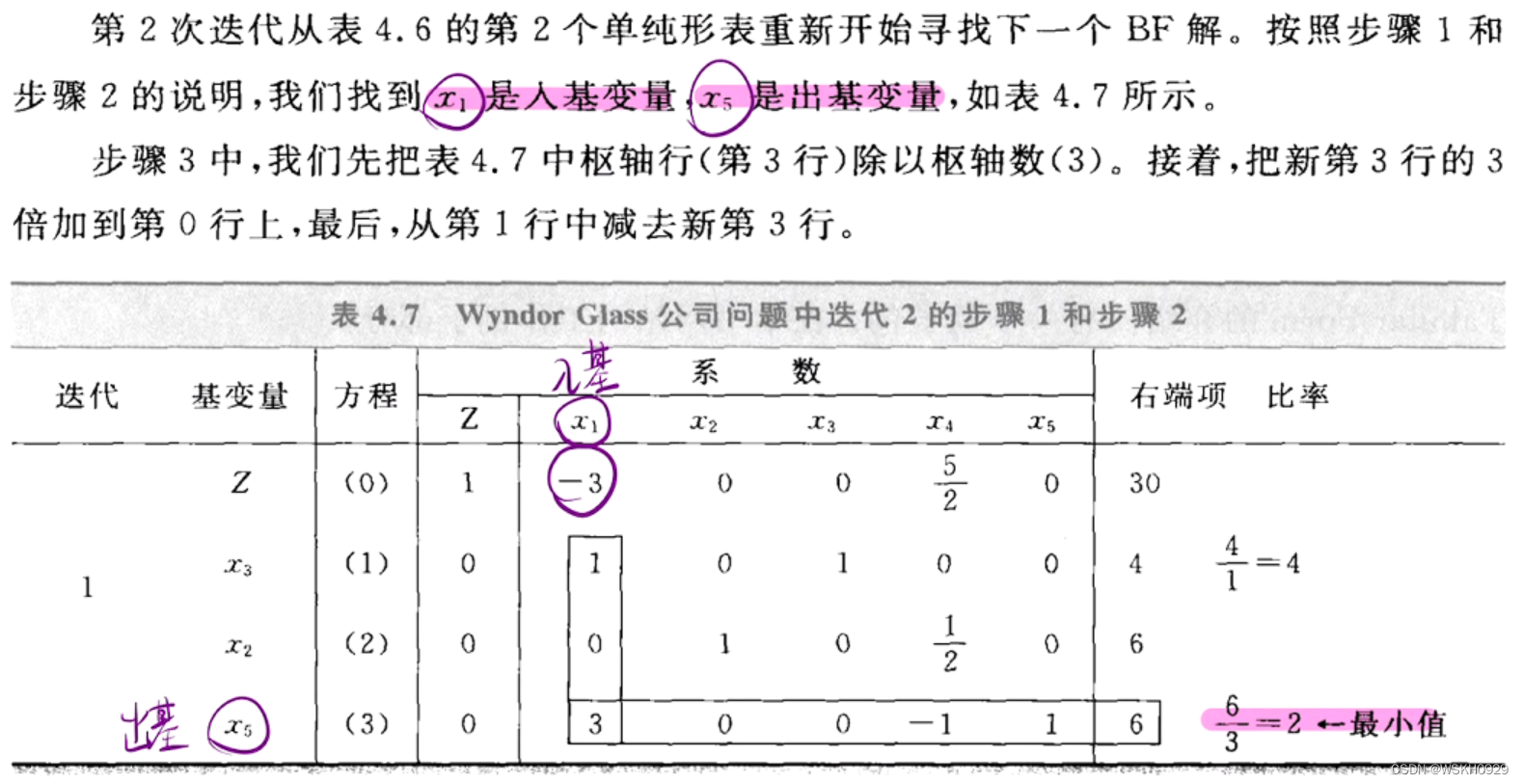
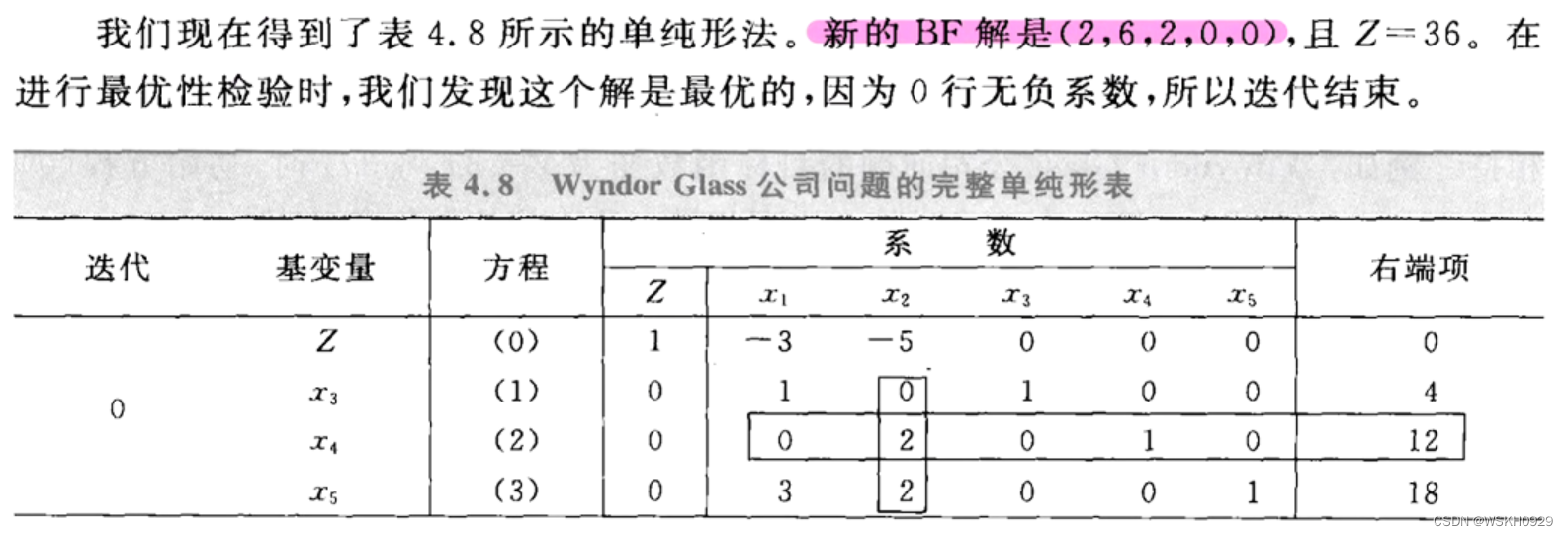
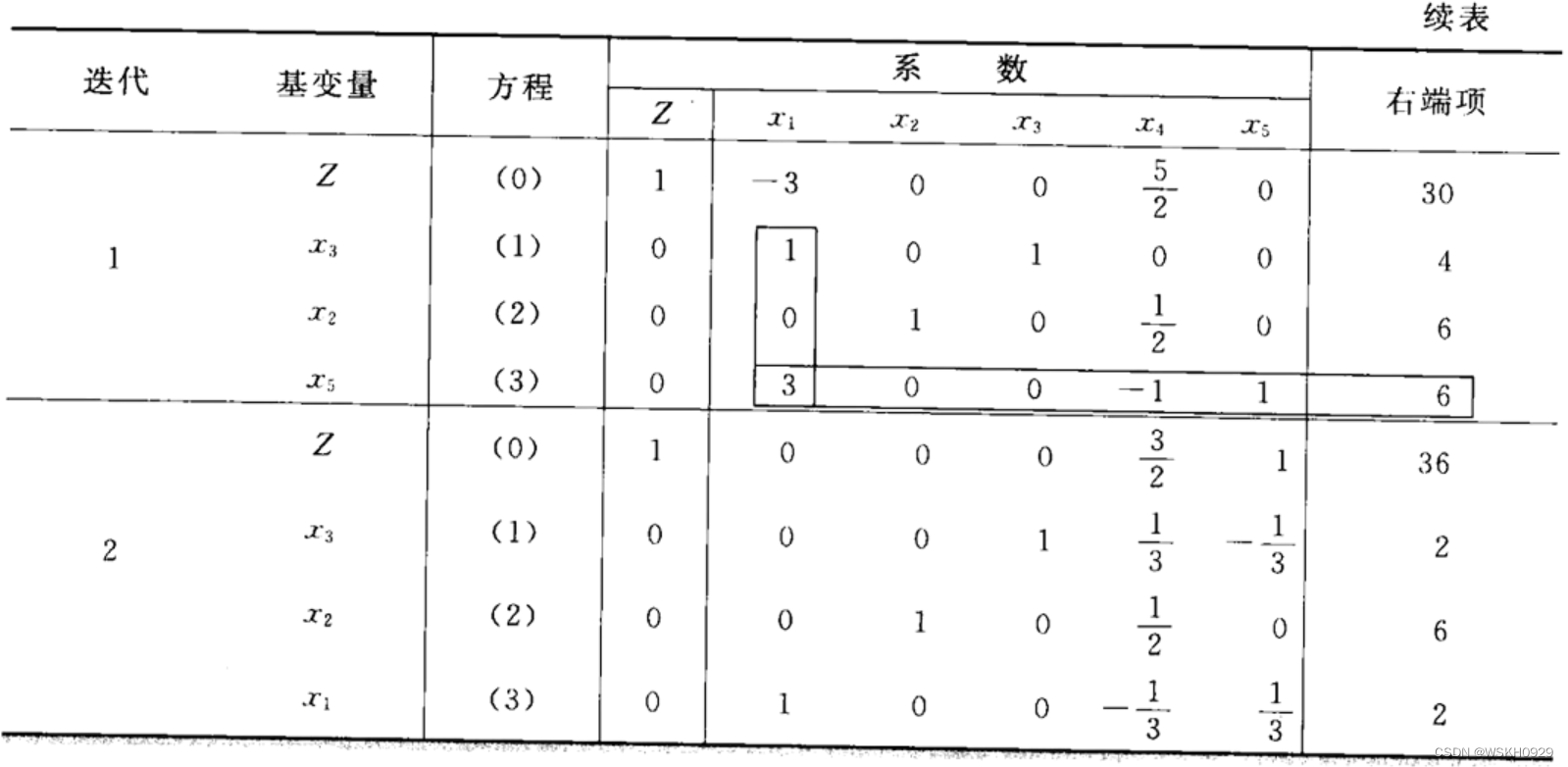

注意,单纯形法的代数和表格两种形式是等价的。当要了解单纯形法背后的逻辑原理时,使用代数形式较好;但表格形式使计算工作更简单、简洁。因此,以后我们一般使用表格形式。
五、单纯形法的突破
如果由于一些相持或其他类似的模糊情况出现,按单纯形法的各种选取规则并无法提供一个明确的选择时应该如何处理?下面我们详细讨论这部分的内容。
5.1 入基变量的相持

5.2 出基变量的相持(退化)

5.3 无出基变量(Z无界)

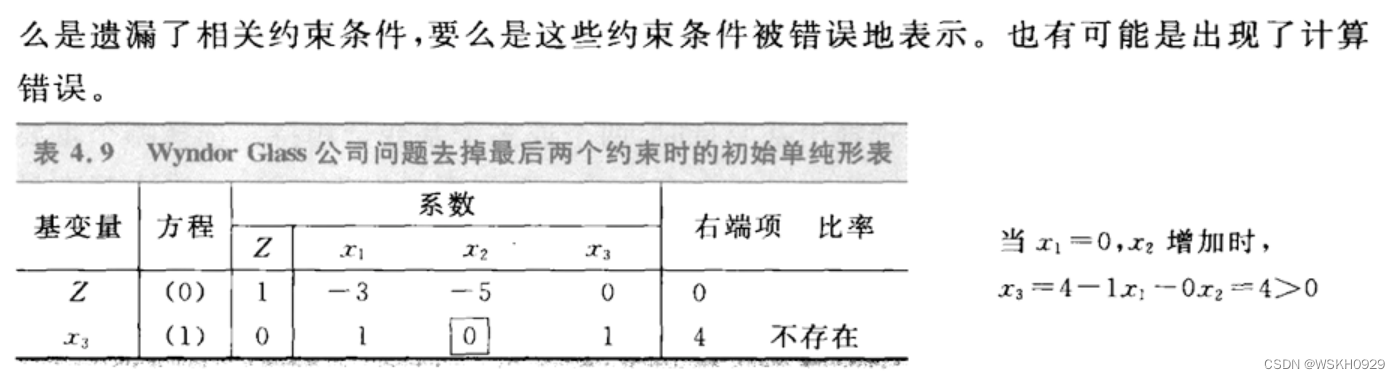
5.4 多个最优解



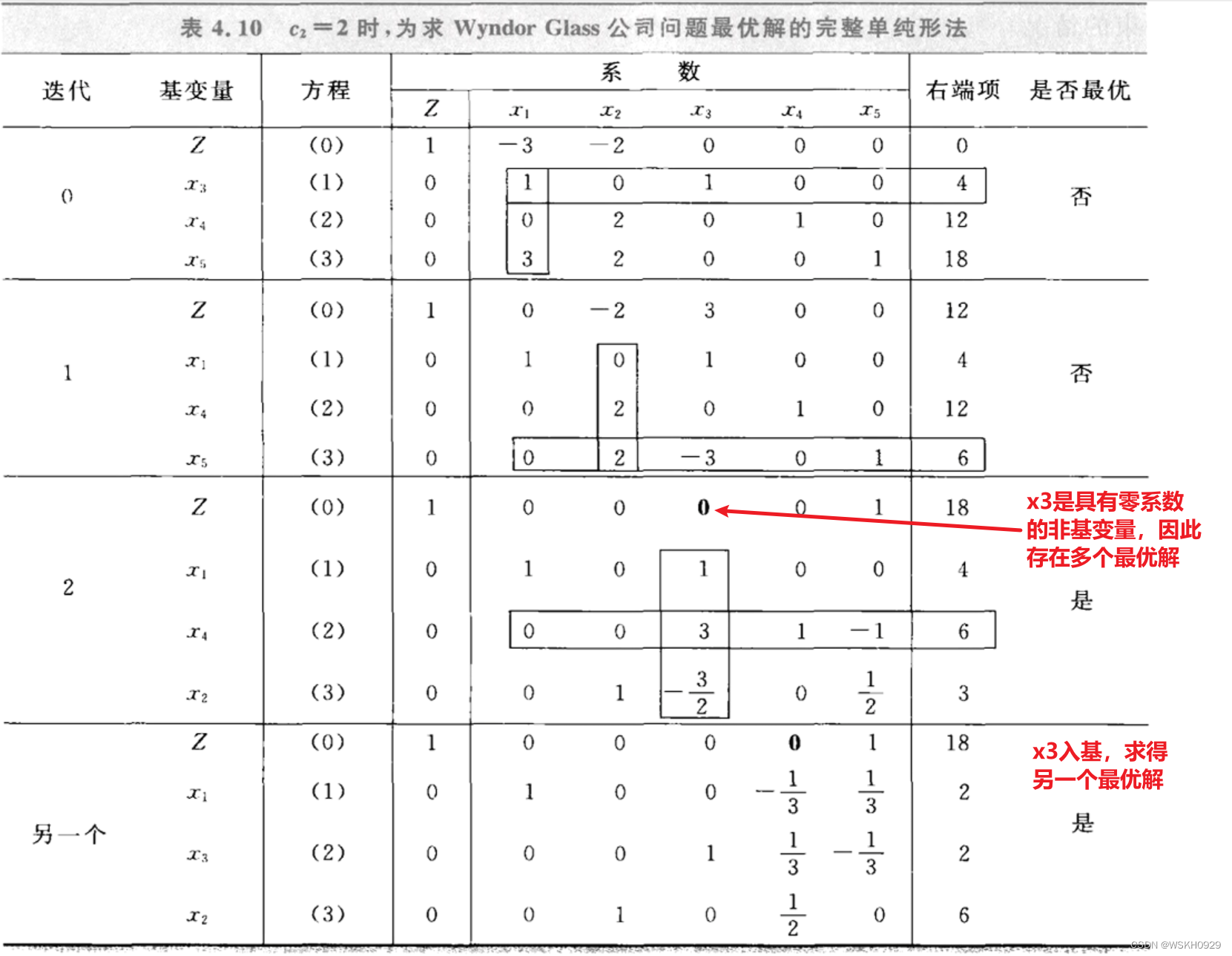
六、改造适用于其他模型形式


6.1 等式约束


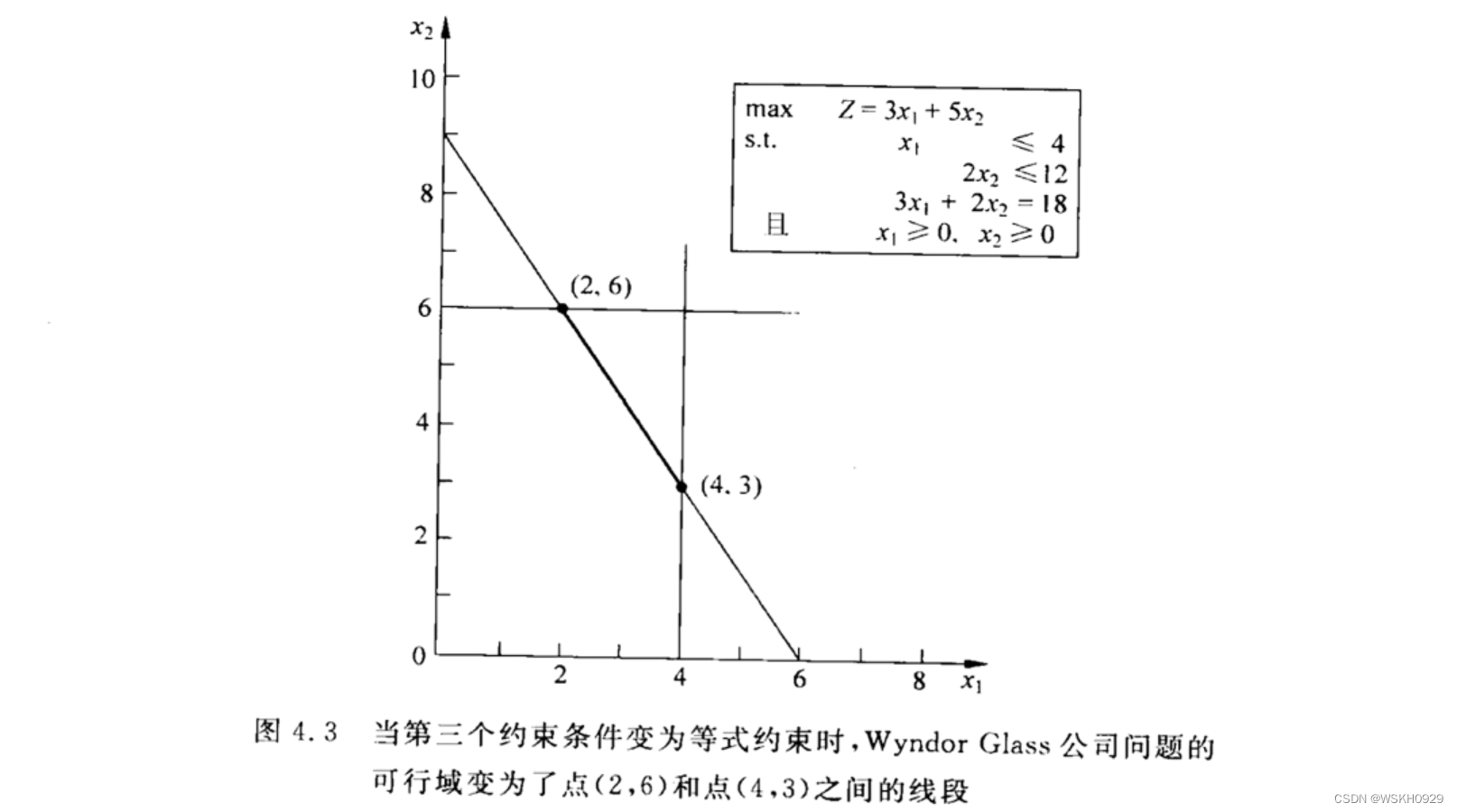

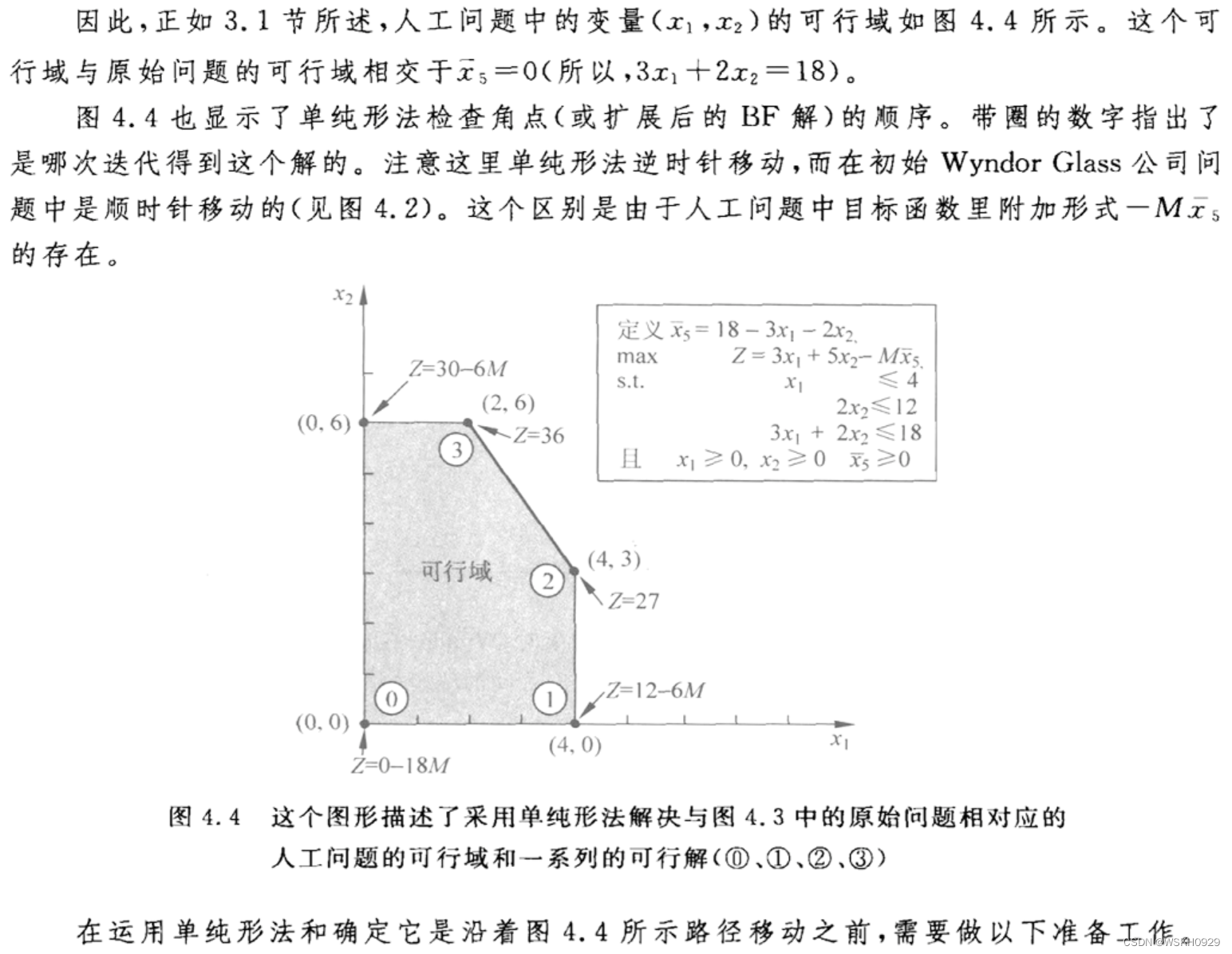


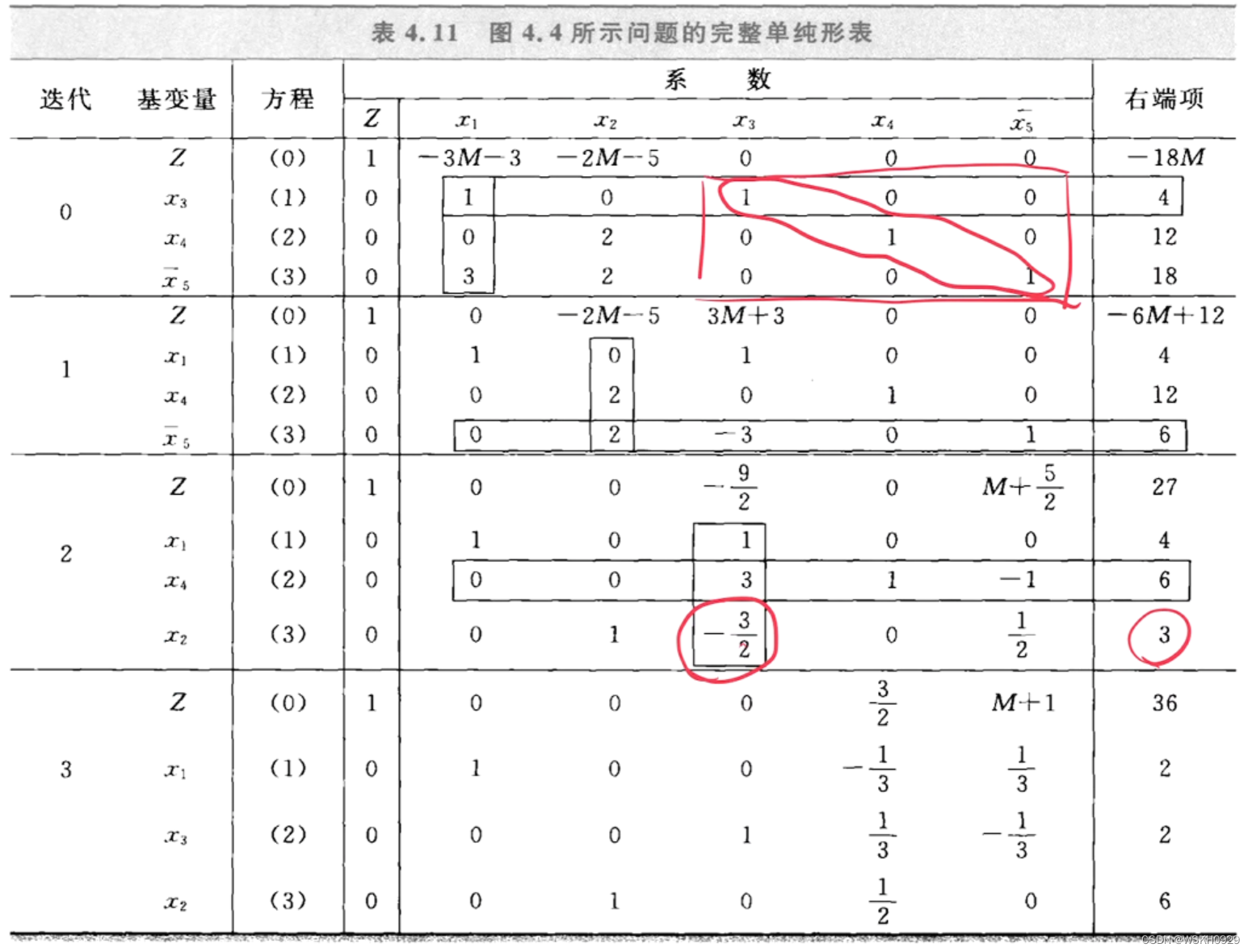
注意:上面举的例子只有一个等式约束。如果一个线性规划模型有多于1个的等式约束,那么每一个都用这种方法处理。
6.2 负的右端项

6.3 大于等于形式的约束条件




6.4 最小化

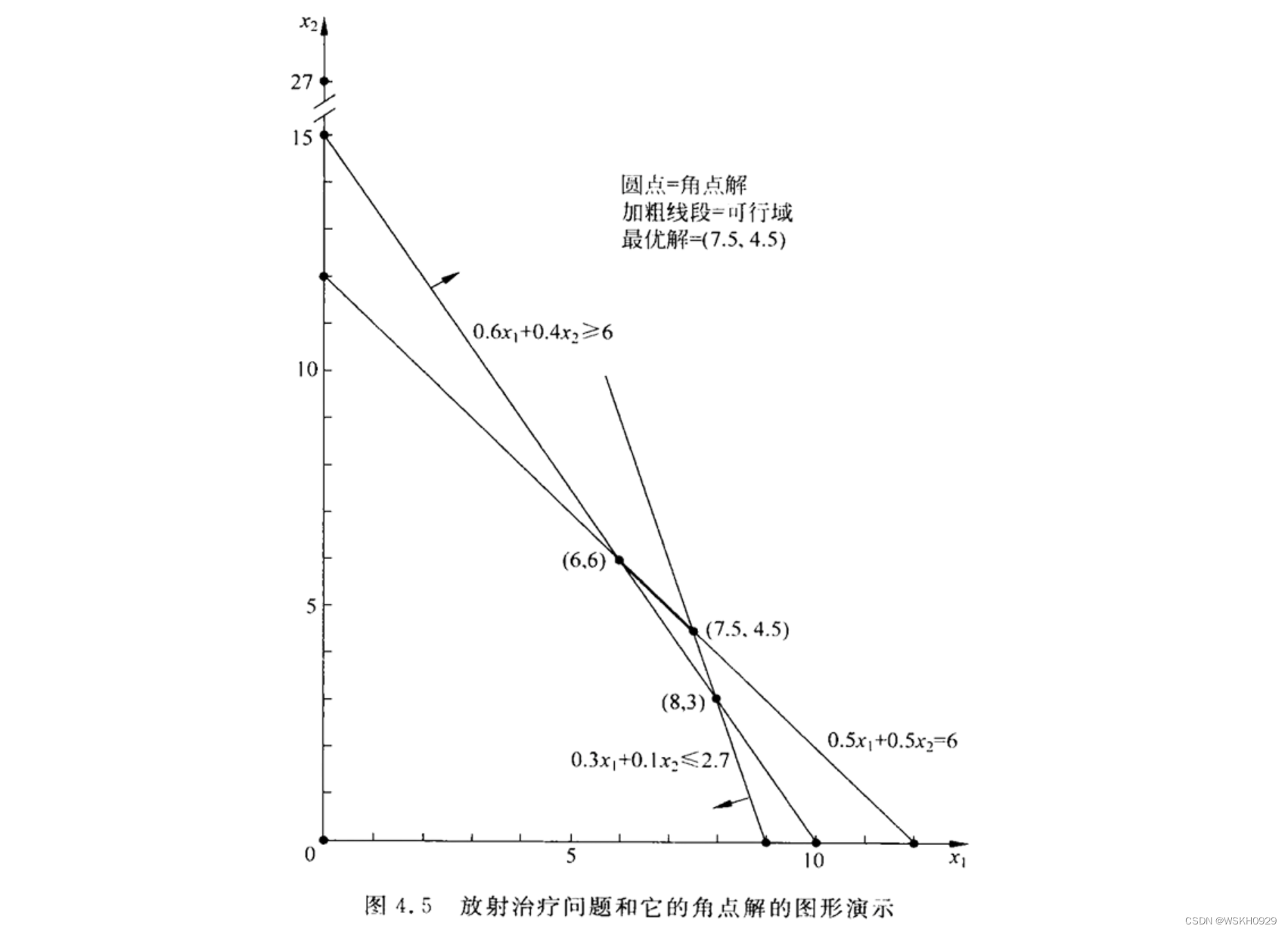
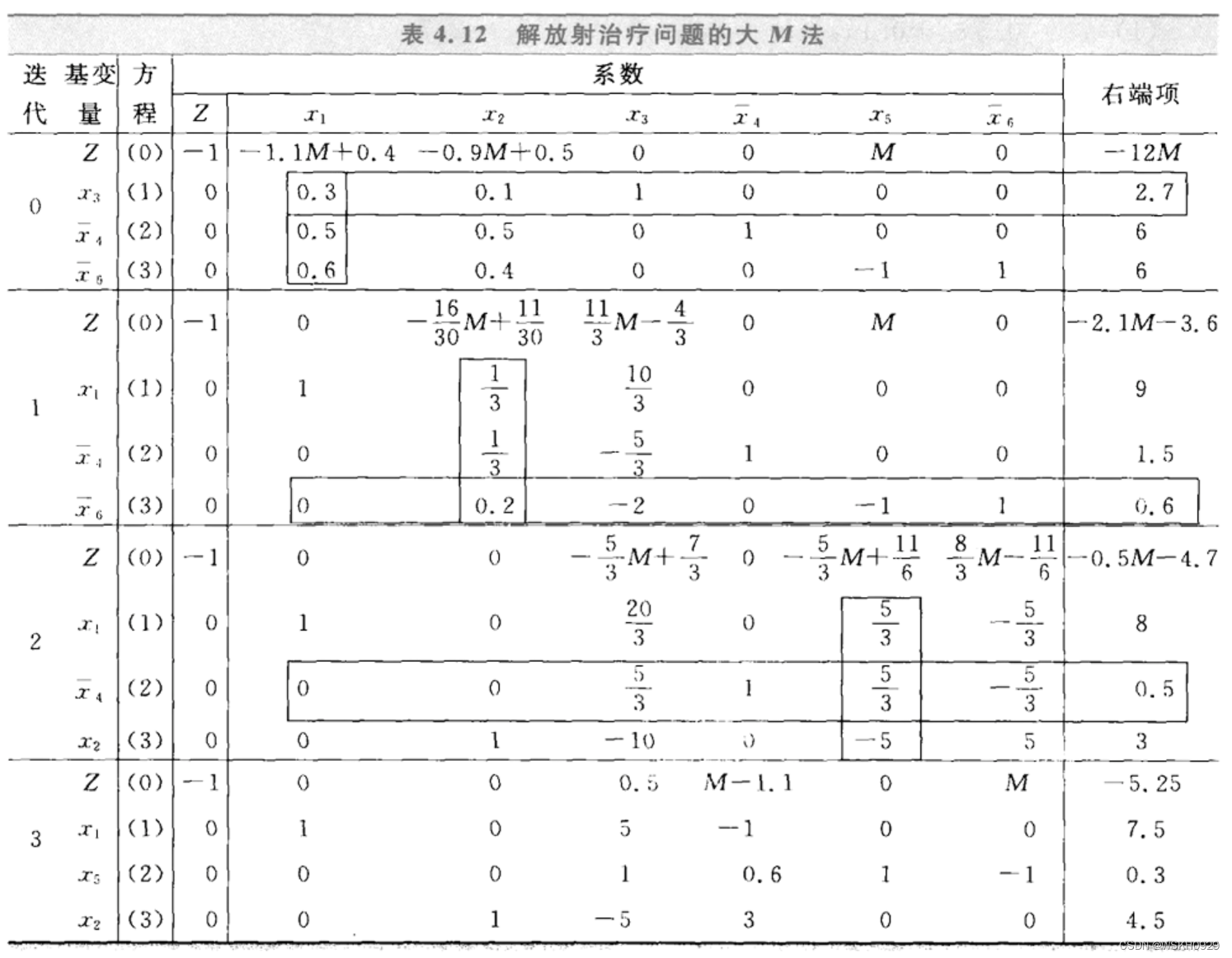
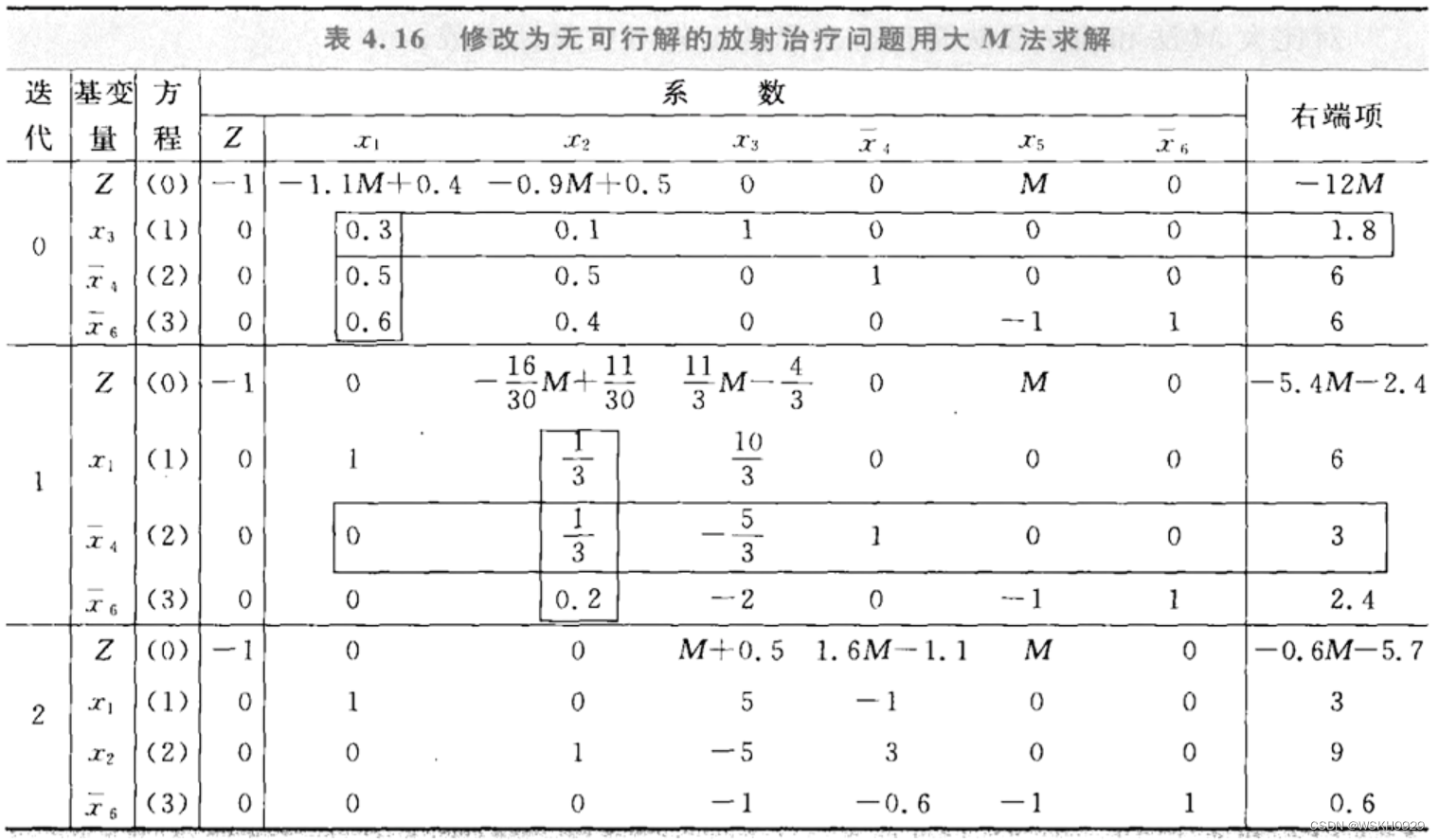
6.5 求解放射治疗的例子




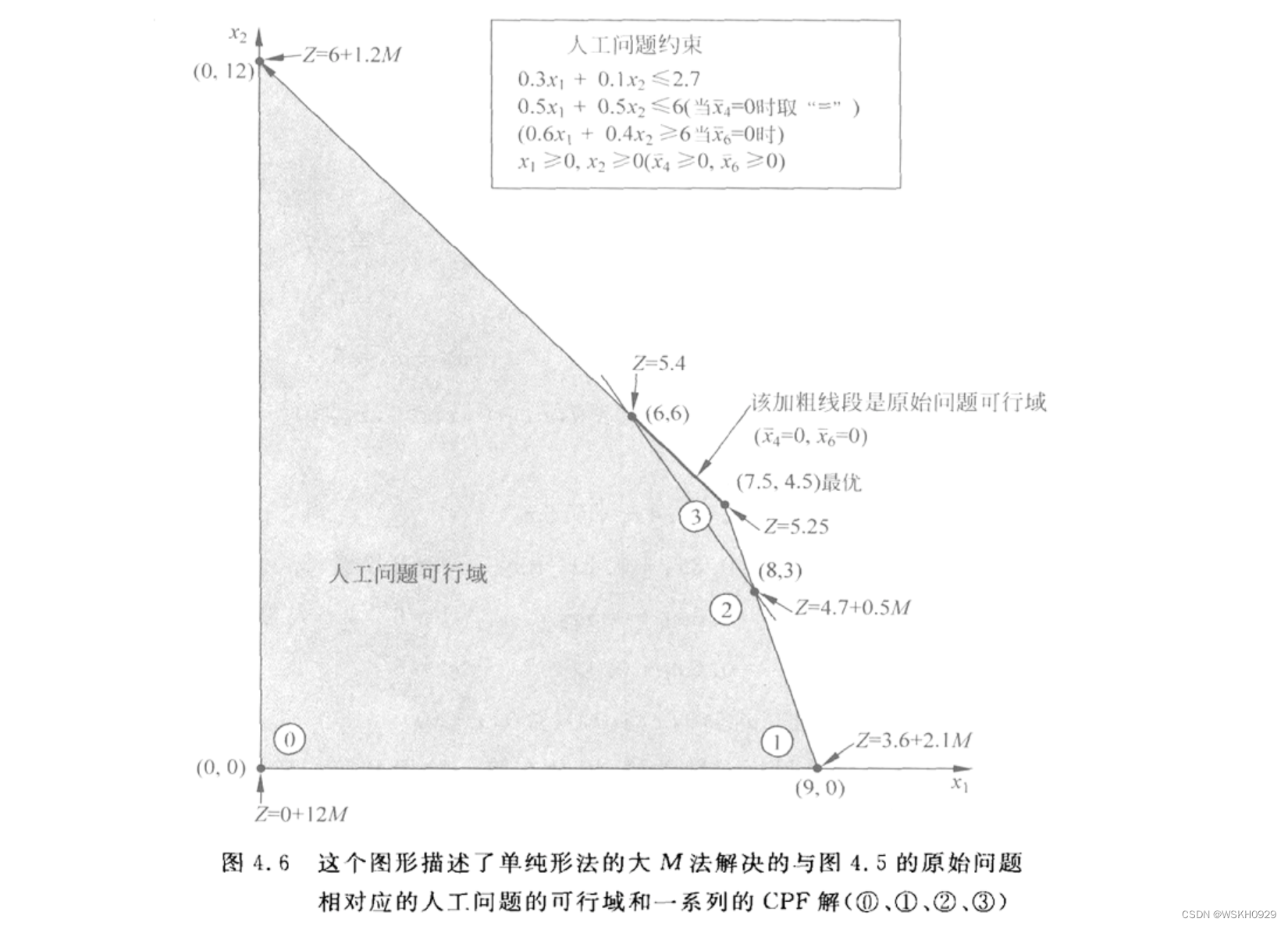
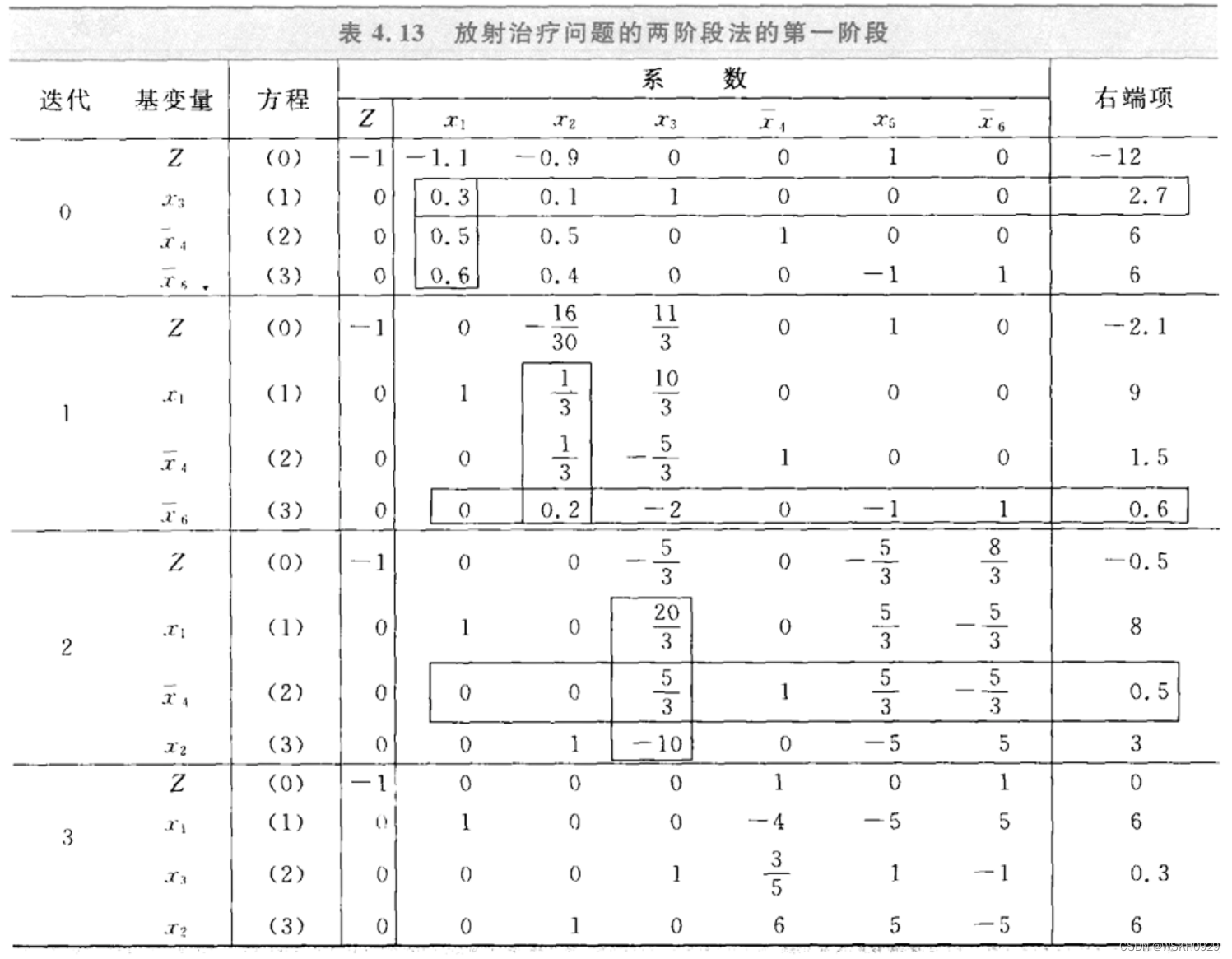
6.6 两阶段法




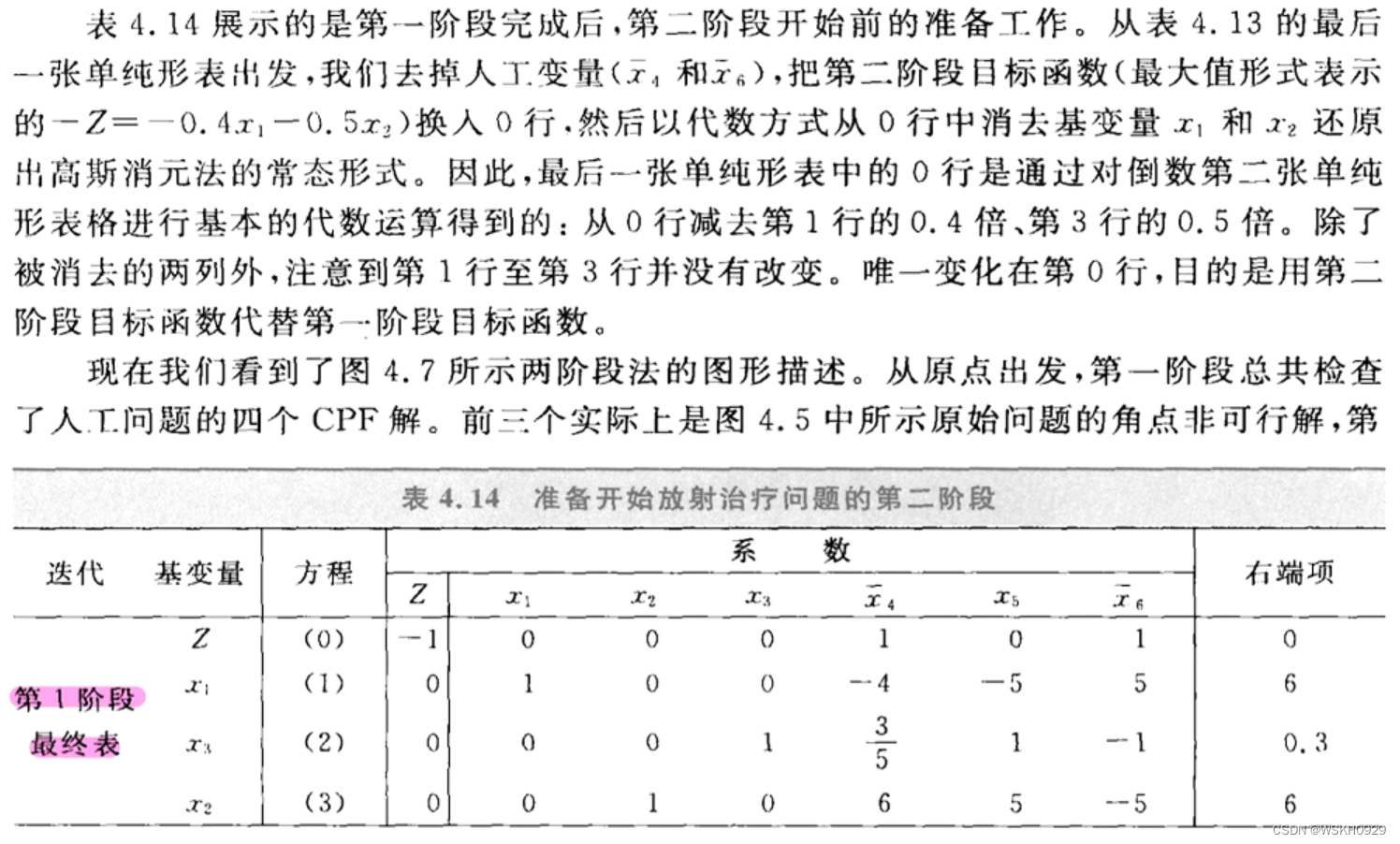
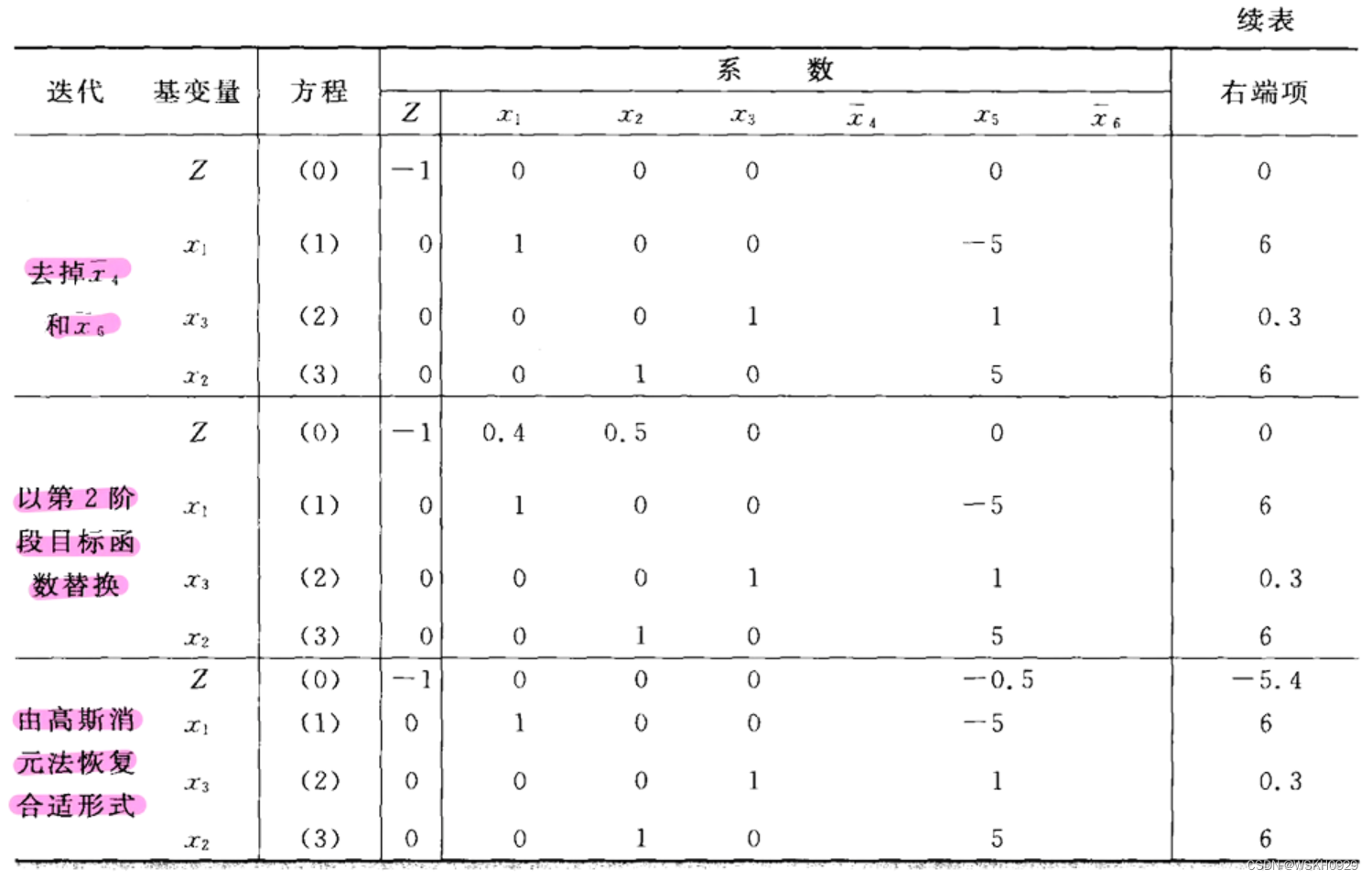
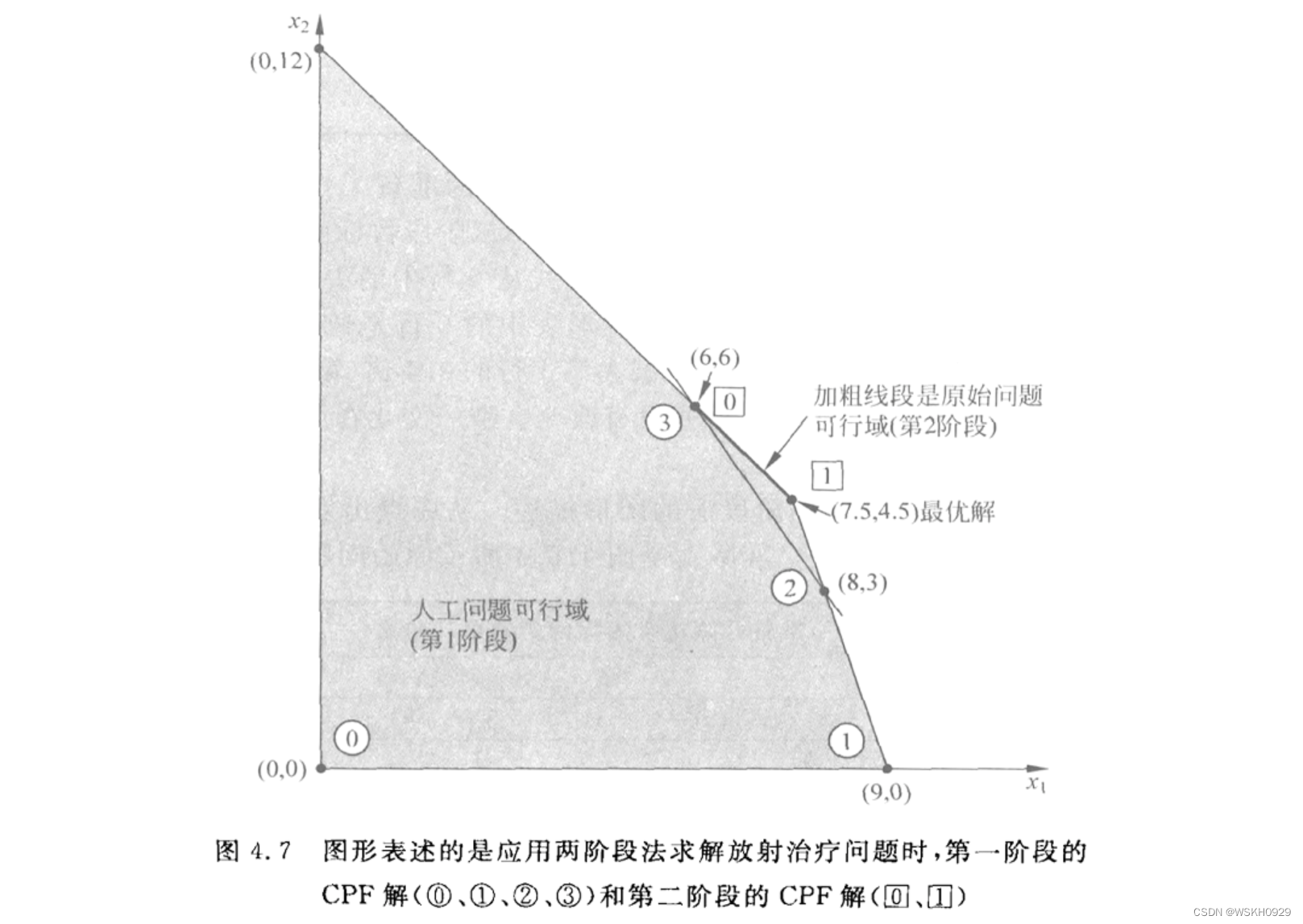
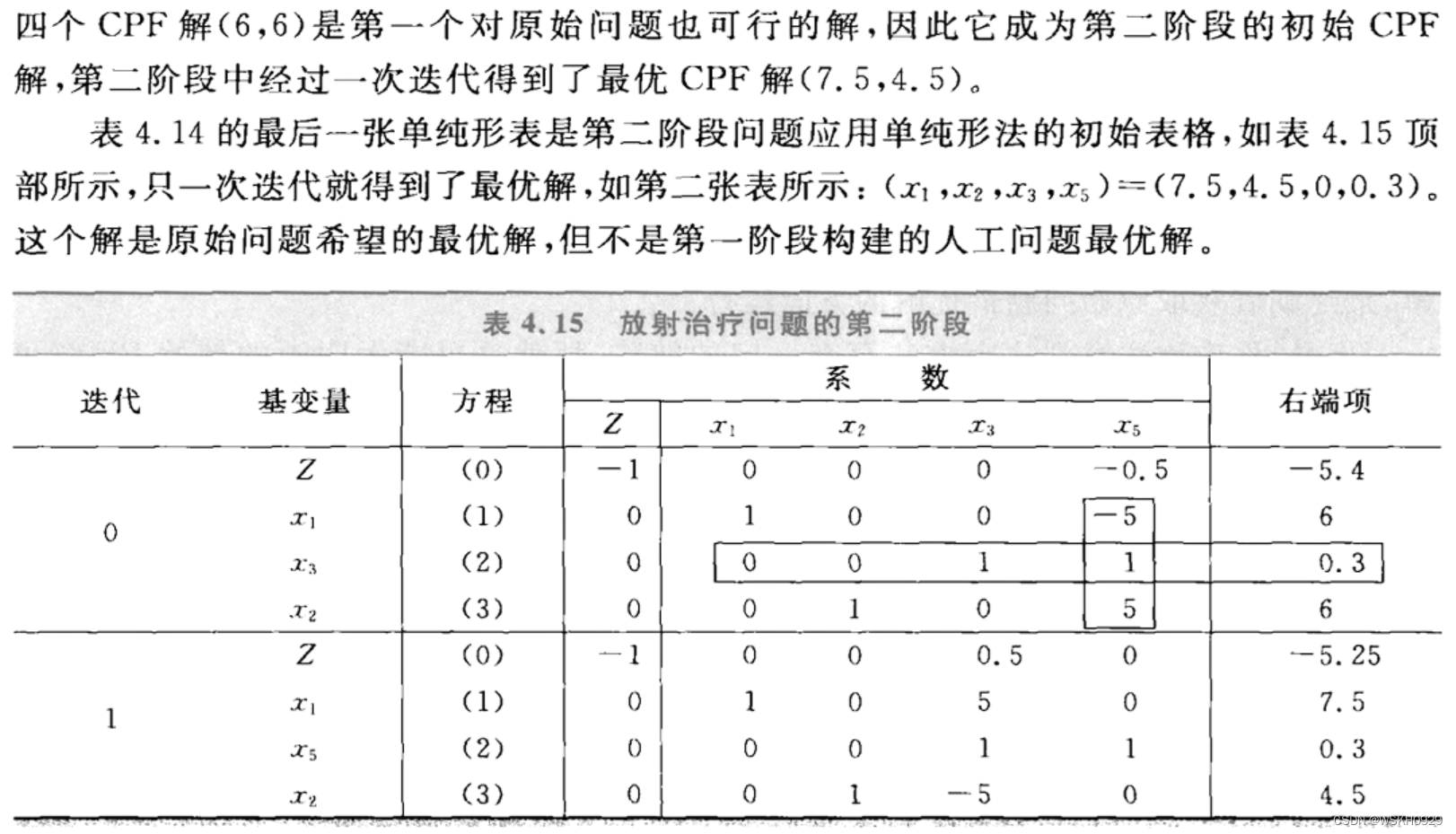

6.7 无可行解

6.8 允许为负的变量

6.8.1 允许为负的有界变量

6.8.2 允许为负的无界变量



七、优化后分析


7.1 再优化
在现实中,找到一个线性规划模型的最优解之后,对该问题略加变化的模型,我们经常需要再次(常常是多次)求解,例如:模型调试阶段、优化后分析阶段。
一种简单的处理方法是,每次变化后,都从头开始运行单纯形法。但是,现实中的线性规划模型通常很大,有成百上千甚至几百万个约束条件和变量。在这样的情况下,每次重新运行单纯形法的方法显得效率较为低下。
一个更有效率的方法是再优化,再优化方法包括:推断如何把模型的变化反映到最终的单纯形表中。如此一来,被修改的单纯形表和原先模型的最优解就可以作为新模型的初始表和初始基本解。如果这个解对新模型是可行的,那么就从该初始BF解开始,照常继续运行单纯形法;如果解不可行,被称为对偶单纯形法的相应算法可能被用来找到新的最优解。这个方法同样是从这个基本解开始进行的,需要注意的是,这里应用对偶单纯形法的要求是修订后的最终表仍能通过最优性检验,如果不能通过,则可由一个被称为原始-对偶(primal-dual)的算法代替。

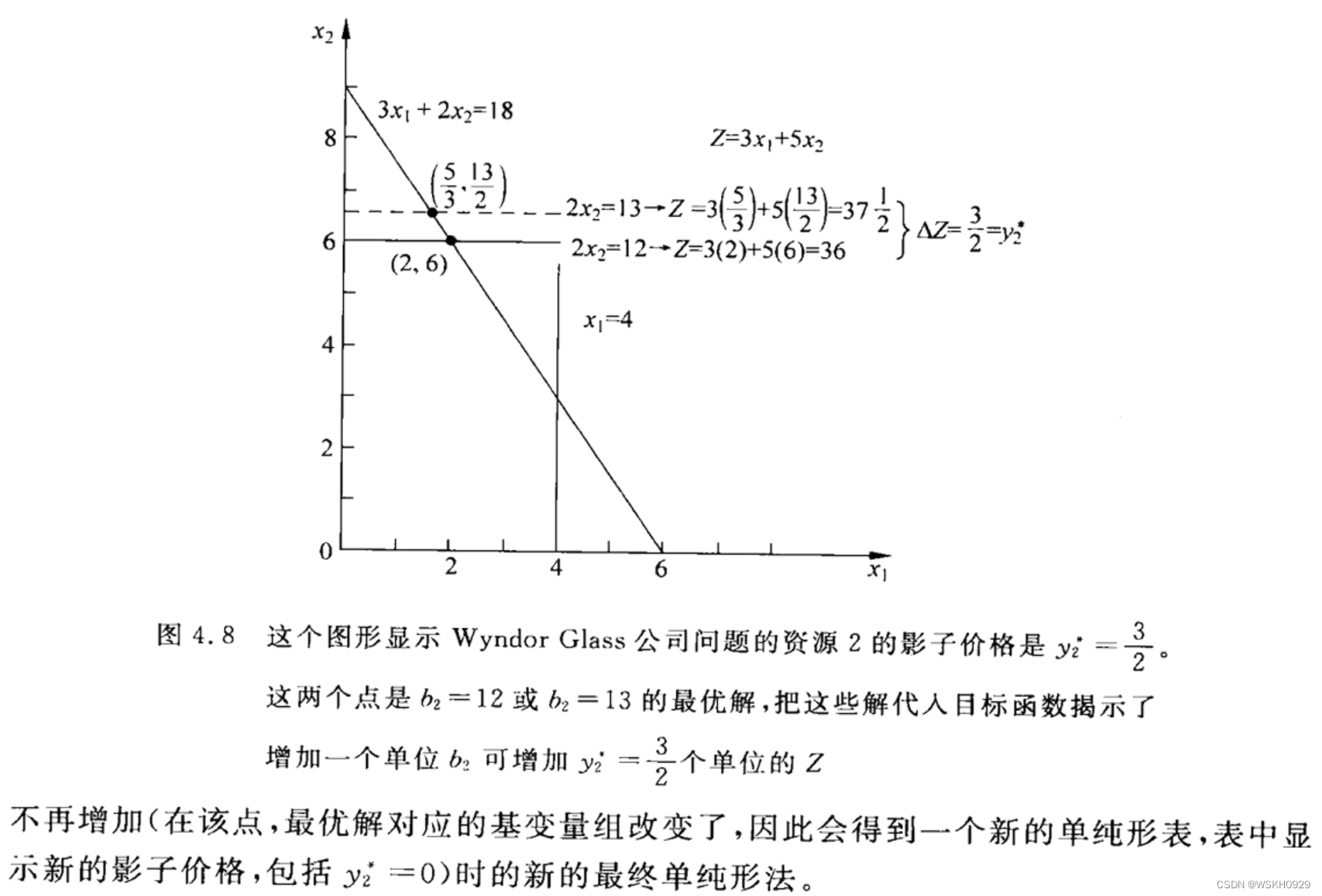
7.2 影子价格





7.3 灵敏度分析





7.4 参数线性规划

